 Le
modèle initial du constructeur est alimenté entre 0 et +5 V et branché
sur la prise A. Un adaptateur contenant les deux résistances additionnelles
permet le branchement sur la prise F. Le potentiel de référence
sera ainsi celui de la terre.
Le
modèle initial du constructeur est alimenté entre 0 et +5 V et branché
sur la prise A. Un adaptateur contenant les deux résistances additionnelles
permet le branchement sur la prise F. Le potentiel de référence
sera ainsi celui de la terre. Assistance technique: P. M. Challou A. Duranteau & S. Hassini
Ce texte de travaux pratiques s'adresse à des élèves de DEUG Scientifique. En raison de contraintes matérielles et horaires, l'enseignement théorique et l'enseignement pratique sont rarement en concordance. Le texte comporte donc les éléments théoriques utiles pour la manipulation. Ils seront présentés sous la forme de "découvertes" que pourrait faire un étudiant avec les connaissances acquises au lycée. On se situera au 17iéme siècle à l'époque d'Huygens et de Newton pour la théorie. Nous utiliserons par contre les moyens informatiques du 21ième sciècle pour l'acquisition et le traitement des données. En TP, la version hypertexte de cette notice lisible avec le navigateur Netscape sera installée sur l'ordinateur mis à votre disposition. Les logiciels d'acquisition et de traitement des données seront commandés directement à partir du navigateur.
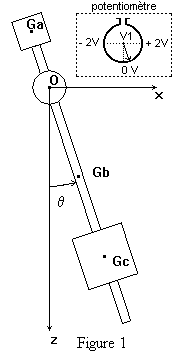
Notre pendule comporte les éléments suivants :
 Le
modèle initial du constructeur est alimenté entre 0 et +5 V et branché
sur la prise A. Un adaptateur contenant les deux résistances additionnelles
permet le branchement sur la prise F. Le potentiel de référence
sera ainsi celui de la terre.
Le
modèle initial du constructeur est alimenté entre 0 et +5 V et branché
sur la prise A. Un adaptateur contenant les deux résistances additionnelles
permet le branchement sur la prise F. Le potentiel de référence
sera ainsi celui de la terre.
Lorsque le pendule est vertical, le potentiomètre devrait se situer à mi-course. Un disque de plastique noir emboîté à force sur l'axe du potentiomètre permet d'ajuster manuellement le zéro électrique et le zéro angulaire. La tension appliquée au potentiomètre est d'environ 8V. Une rotation de 90° devrait correspondre à une tension de 2 Volts sur le curseur du potentiomètre.
Dans la partie supérieure de la tige, une rainure circulaire située à 8,5 cm de l'extrémité, permet de placer l'axe de rotation à 20 cm du centre de gravité Gb de la tige. Dans la partie inférieure, 27 rainures circulaires régulièrement espacées de 1 cm, qui permettent de positionner précisément le centre de gravité Gc du cylindre (c) à une distance rc de l'axe de rotation qui peut varier de 20 à 46 cm. L'extrémité des vis de blocage est conique.
Le dispositif d'accquisition de données comporte:
L'interface Orphy-GTI possède entre autres les caractéristiques suivantes:
Nous n'utiliserons dans cette manipulation que l'entrée EA2 sur la prise F
Le logiciel GTI.exe permet de programmer l'interface Orphy GTI et déclenche les acquisitions. Les mesures mises en mémoire dans le boîtier sont ensuite transmises à l'ordinateur et affichées sur l'écran. Pour un traitement complet, les mesures sont transférées au logiciel Régressi Windows. Nous l'utiliserons pour représenter les courbes V1(t) puis q(t) des mouvements du pendule. Ses possibilités de modélisation fourniront une mesure précise des périodes et de l'amplitude des oscillations. Toutes les applications numériques comme les calculs du moment d'inertie du pendule composé et de la valeur théorique de la période.seront effectuées dans la page expression de Régressi. Vous trouverez sur la version hypertexte de cette notice, des séquences d'apprentissage montrant très explicitement le fonctionnement des deux logiciels.
Au lycée, en première S puis en terminale S vous avez déjà acquis des notions de mécanique du point et du solide. Vos connaissances de lycéen devraient suffire pour "découvrir" quelques éléments de mécanique du solide utiles pour cette manipulation. Le texte qui suit ne remplace pas un véritable cours. Vous avez étudié le pendule simple.
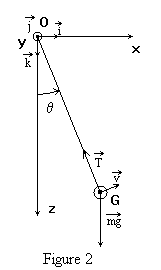 Une bille
assimilable à un point matériel G de masse m est suspendue à
un point fixe O par un fil de longueur l. La bille oscille dans un plan vertical.
Soit Oz un axe vertical descendant. L'angle q
est défini sur la figure ci-dessous.
Une bille
assimilable à un point matériel G de masse m est suspendue à
un point fixe O par un fil de longueur l. La bille oscille dans un plan vertical.
Soit Oz un axe vertical descendant. L'angle q
est défini sur la figure ci-dessous.
En première S vous avez défini l'énergie cinétique, l'énergie potentielle et l'énergie mécanique. Vous travaillez dans un référentiel supposé galiléen.
![]()
Les frottements sont négligeables, l'énergie mécanique
Em est constante: ![]()
La dérivée par rapport au temps de l'énergie mécanique est donc nulle:
![]()
![]()
C'est ainsi que vous avez obtenu l'équation différentielle du mouvement en classe de terminale S.
Le deuxième terme ressemble beaucoup à l'expression du moment du poids par rapport à l'axe de rotation. Pour mieux l'exprimer, il serait judicieux d'utiliser le produit vectoriel que vous avez également découvert en terminale pour exprimer la force de Lorentz.
![]()
![]()
![]()
Ici aussi nous pouvons faire apparaître un produit vectoriel:
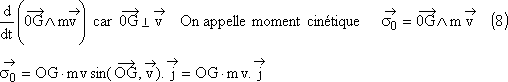
![]()
Nous aurions pu obtenir l'équation initiale par application du théorème
du moment cinétique "découvert" ci dessus. Les vecteurs
sont portés par l'axe 0y sur lequel:
![]()
Le produit ml2, qui sera appelé moment d'inertie IOy
du point matériel de masse m par rapport à l'axe de rotation
0y joue un rôle comparable à celui de la masse d'inertie m dans la
R.F.D.
Si les oscillations sont de faible amplitude, on peut remplacer sin(q) par sa valeur q en radians. L'équation différentielle se simplifie et devient:
![]()
La solution revient à chercher une fonction du temps qui dérivée
deux fois restitue à un facteur près la même fonction.
![]()
![]()
![]()
![]()
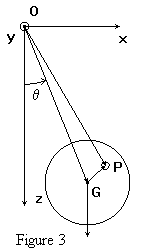 Remplaçons
le fil par une tige rigide de masse négligeable et le point matériel
par un disque vertical de rayon R fixé en son centre G sur la tige . Un
axe de rotation horizontal avec roulements à billes fixé sur la
tige permet des oscillations libres du pendule. Le disque est homogène,
sa masse surfacique sera notée s et sa
masse totale m. Le disque peut donc être découpé en une multitude
de petits éléments de surface dS et de masse dm= sdS
situés à la distance OP de l'axe de rotation .
Remplaçons
le fil par une tige rigide de masse négligeable et le point matériel
par un disque vertical de rayon R fixé en son centre G sur la tige . Un
axe de rotation horizontal avec roulements à billes fixé sur la
tige permet des oscillations libres du pendule. Le disque est homogène,
sa masse surfacique sera notée s et sa
masse totale m. Le disque peut donc être découpé en une multitude
de petits éléments de surface dS et de masse dm= sdS
situés à la distance OP de l'axe de rotation .
Au cours du mouvement, la vitesse angulaire de tous les points sera la même.
Le premier terme de l'équation différentielle du mouvement s'écrira
donc:
![]()
On supposera ici que vous avez déjà découvert le produit scalaire.
![]()
![]()
On peut associer à chaque point P son symétrique par rapport à G. La somme des produits scalaires correspondants est nulle. Le dernier terme est donc nul.
 Le
deuxième terme est tout simplement le moment d'inertie IGy du
disque par rapport à un axe Gy parallèle à Oy. Ce moment
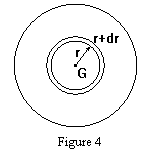
d'inertie est facile à calculer en découpant le disque en couronnes
circulaires de rayon r et de largeur dr:
Le
deuxième terme est tout simplement le moment d'inertie IGy du
disque par rapport à un axe Gy parallèle à Oy. Ce moment
d'inertie est facile à calculer en découpant le disque en couronnes
circulaires de rayon r et de largeur dr:
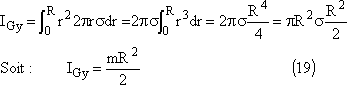
Le moment d'inertie par rapport à l'axe Oy sera donc
![]()
Vous venez de "découvrir" le théorème d'Huygens qui sous sa forme générale s'énonce de la façon suivante:
Le moment d'inertie d'un solide par rapport à un axe Oy est égal au moment d'inertie par rapport à un axe Gy parallèle à l'axe Oy passant par le centre de masse du solide augmenté du produit de la masse de ce solide par le carré de la distance du centre de masse à l'axe Oy.
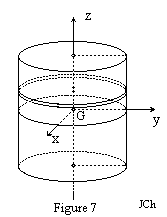
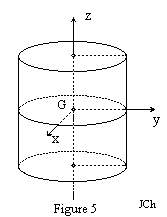 Tous
les éléments qui constituent notre pendule sont des cylindres de
révolution. Soit G le centre de gravité d'un cylindre C et et Gxyz
un système d'axes orthonormé centré en G. Gz coïncide
avec l'axe de révolution de C. Les axes Gy et Gx jouent des rôles
identiques. Les moments d'inertie IGy et IGx par rapport
à ces axes sont donc égaux et s'écrivent:
Tous
les éléments qui constituent notre pendule sont des cylindres de
révolution. Soit G le centre de gravité d'un cylindre C et et Gxyz
un système d'axes orthonormé centré en G. Gz coïncide
avec l'axe de révolution de C. Les axes Gy et Gx jouent des rôles
identiques. Les moments d'inertie IGy et IGx par rapport
à ces axes sont donc égaux et s'écrivent:
![]()
![]()
![]()
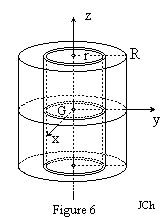
La première intégrale est en fait le moment d'inertie du cylindre par rapport à l'axe Gz:
![]()
Elle se calcule aisément en en découpant le cylindre en cylindres élémentaires d'axe Gz de rayon r, d'épaisseur dr et de hauteur h:
![]()
![]()
La deuxième intégrale se calcule
facilement en découpant le cylindre en tranches d'épaisseur dz perpendiculaires
à l'axe Gz.
 La
masse la tranche élémentaire sera:
La
masse la tranche élémentaire sera:
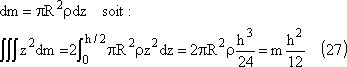
Le moment d'inertie d'un cylindre par rapport à un axe perpendiculaire à son axe de révolution s'écrit donc:
![]()
Si le cylindre est creux:
![]()
![]()
Exprimons les moments d'inertie des trois principaux cylindres qui constituent le pendule pesant et appliquons pour chacun le théorème d'Huygens. Le moment d'inertie par rapport à l'axe de rotation Oy du pendule s'écrira donc:
![]()
Nous avons négligé le moment d'inertie du cylindre qui assure la fixation sur l'axe de rotation.
La formule paraît un peu longue, mais avec Régressi Windows l'application numérique ne présentera aucune difficulté.
 Pour
obtenir l'équation différentielle du mouvement du pendule pesant,
exprimons la somme des moments par rapport à Oy des forces de pesanteur
appliquées aux centres de gravités Ga, Gb et Gc des trois principaux
élèments du pendule pesant.
Pour
obtenir l'équation différentielle du mouvement du pendule pesant,
exprimons la somme des moments par rapport à Oy des forces de pesanteur
appliquées aux centres de gravités Ga, Gb et Gc des trois principaux
élèments du pendule pesant.
![]()
Si les oscillations sont de faible amplitude l'équation différentielle du mouvement s'écrit:
![]()
![]()
La solution est de la forme:![]()
avec ![]()
et ![]()
La valeur théorique de T0 sera calculée facilement dans la page expressions de Régressi Windows. Nous la comparerons à la valeur expérimentale.
Si l'amplitude des oscillations dépasse une dizaine de degrés, on ne peut plus confondre sin(q) avec q . L'équation différentielle sera résolue numériquement par Régressi Windows:
![]()
La solution est périodique mais elle n'est plus tout à fait sinusoïdale. Ici encore vous comparerez les résultats "théoriques" aux résultats expérimentaux.
Une ailette fixée au sommet du cylindre (a) freine le mouvement. On suppose que le moment de freinage correspondant est proportionnel à la vitesse de rotation.
![]()
Si les angles sont petits et si la valeur du coefficient de frottement F est faible:
![]()
la solution est de la forme:
![]()
La modélisation avec Régressi donnera très facilement la constante de temps t.
Connaissant I nous pourrons donc évaluer la valeur de F :
![]()
On vous demandera en TP de calculer la contribution au moment d'inertie total de la plaque de plastique rectangulaire. Les dimensions et la masse seront indiquées. Préparez la formule correspondante que vous êtes tout à fait capable de démontrer. La réponse à cette question sera décisive pour la note finale de votre compte rendu de TP.
Les frottements solides sont caractérisés par une décroissance linéaire de l'amplitude des oscillations. Dans le dispositif Pendulor les frottements solides localisés dans le potentiomètre sont généralement prépondérants. Par analogie avec l'étude effectuée avec le pendule élastique horizontal, nous supposerons qu'un moment de module constant noté Gs s'oppose au mouvement de rotation.
L'instruction sign(v) sera utilisée avec Régressi : sign(v)= +1 si v >0 ; sign (v) = -1 si v<0
![]()
Si les angles sont petits:
![]()
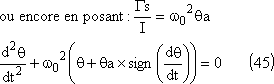
La solution de cette équation différentielle est en tous points comparable à celle proposée pour le pendule élastique horizontal. On pourra donc s'y reporter.
De même les droites qui joignent les maxima ou minima sont respectivement:
![]()
Dans des conditions de test toujours identiques la valeur déterminée pour qa caractérisera "la qualité" du potentiomètre sans "frottements"