pendule simple: manipulation

3 MANIPULATION

3.1 Matériel expérimental

Un ordinateur PC W98 avec imprimante.
Une interface Orphy GTI.
Un dispositif pendulor avec ses accessoires et boitier adaptateur pour branchement sur la prise F.
3.2 Première acquisition

Mettez l'ordinateur et l'interface Orphy GTI sous tension. Vérifiez que le câble d'alimentation et de mesure de pendulor est bien branché latéralement sur la prise F de GTI à travers le boîtier adaptateur.

Sur le bureau de l'ordinateur cliquez sur l'icône Pendulor. Le Navigateur s'installe et vous présente l'introduction du texte de manipulation. Dans la table des matières, à gauche cliquez sur 3 MANIPULATION pour voir apparaître ce paragraphe. Vous pouvez fermer votre polycopié, la notice hypertexte (html) prend la suite. Vous lancerez les applications à partir du navigateur et travaillerez parfois avec trois applications simultanément en passant de l'une à l'autre par la commande Alt Tab ou avec la souris en cliquant dans la barre des tâches. Vous avez le choix:

3.3 Calcul numérique de la période du pendule

La réussite de ce calcul conditionne la suite du TP. Il importe donc que celui-ci soit effectué de façon très lisible dans la page expressions de Régressi. Comme votre expérience du logiciel est limitée, tout sera fait pour assurer la réussite de ce calcul. Il importe de respecter impérativement les notations proposées.

Les commentaires sont les bienvenus et sont précédés par une apostrophe. Un caractère souligné sépare la valeur numérique de l'unité. On utilisera toujours l'unité de base du système international. On exprime par exemple la masse en kg pas en g, les longueurs en m pas en cm ou mm. La Syntaxe de formules est simple et classique. Un mémo d'aide est disponible . Les caractères grecs sont obtenus en pressant la touche Ctrl et le caractère souhaité.

Voici une présentation que vous devriez adopter en vérifiant soigneusement les valeurs car les pendules ne sont pas tout à fait identiques.

ATTENTION : le copier coller d'Internet Explorer vers Régressi conduit à des résultats catastrophiques. Vous devrez donc taper vous même les instructions ci dessous:

Dans la page , onglet expressions, pressez si nécessaire

'Calcul de T0

'cylindre a téflon
Ma=19.6E-3_kg
ha=3.6E-2_m
Ra=10E-3_m
ra=85E-3_m
Ia=Ma*(ra^2+ha^2/12+Ra^2/4)
'cylindre b : la tige
Mb=43E-3_kg
hb=57E-2_m
Rb=3E-3_m
rb=20E-2_m
Ib=Mb*(rb^2+hb^2/12+Rb^2/4)
'cylindre c coulissant
Mc=143E-3_kg
hc=3.1E-2_m
R2=14E-3_m
R1=3E-3_m
rc=45E-2_m
Ic=Mc*(rc^2+hc^2/12+(R2^2+R1^2)/2)
I=Ia+Ib+Ic
g=9.81_m.s-2
T0=2*p*SQRT(I/g/(Mb*rb-Ma*ra+Mc*rc))

Si vous avez trop de difficultés (première prise de contact avec Régressi ) allez dans Fichiers et cliquez importer traitements de :\Regressi\documents\pendulor.rw3

Vérifiez les valeurs numériques

Pressez F2 ou cliquez sur mise à jour pour effectuer les calculs. Normalement la valeur calculée est très proche de la valeur mesurée ( < 1%)
Enregistrez votre fichier sous: C:\Regressi\documents\votrenom1.rw3
Vous imprimerez exclusivement en passant par la commande: Fichier Imprimer
Cochez comme ci-contre,cochez Expressions, et dans la zone imprimer date et en-tête . Lancez l'impression.
Pour commenter utilement votre résultat, dans le bas de la page étudiez l'importance respective des termes. Quels sont ceux que nous aurions pu négliger?
Laissez Régressi Windows et GTI.exe ouverts sans rien changer.

3.4 Oscillations anharmoniques

Pour les angles supérieurs à 8 ou 9°, il faut remplacer q par sin(q) dans l'équation différentielle. Il n'est plus possible de donner une solution analytique simple. On montre que si les angles ne sont pas trop grands:

Laissez le cylindre coulissant sur rc = d = 0.45 m
Vous allez enregistrer 12 pages de mesures avec des valeurs croissantes de V1:
Dans GTI. cliquez
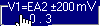
changez le calibre puis
Inclinez le pendule jusqu'à V1= 0.2V, lâchez, enregistrez et transmettez à Régressi en nouveau Fichier et indiquez en commentaire la tension V1
Revenez dans GTI. Inclinez le pendule jusqu'à V1=0.4V lachez, transmettez en nouvelle page etc pour 0.6; 0.8; 1.0; 1.2; 1.4; 1.6; 1.8; 2.0; 2.2; jusqu'à 2.4 V en changeant de calibre si nécessaire.
Dans Régressi, dans grandeurs onglet Expressions ajoutez:
q= V1*p/4_rad et T0=......._s , la période mesurée en 3.3 pour les petits angles

Pressez F2 ou mise à jour.
Dans la page Graphique N°1 puis
affichez q en fonction de t
Modélisez q avec le modèle prédéfini sinusoïde pure
q(t)= a + b*sin(2*p/T*t+j) et

En effet, bien que les courbes enregistrées ne soient plus tout à fait sinusoïdales, elles restent périodiques. La modélisation par une sinusoïde pure permet cependant d'obtenir la période T du fondamental et l'amplitude maximale qmax=b

Continuez dans les 11 pages suivantes jusqu'à
Enregistrez votre fichier sous: C:\Regressi\documents\votrenom2.rw3
Régressi a mémorisé dans un tableau toutes les valeurs obtenues pour les paramètres dans chaque page.
Si nécessaire, reclassez les pages en pressant le bouton trier en haut à droite ou encore en cliquant Pages, Tri par rapport à un paramètre. Si une mesure est manifestement mauvaise, affichez la page correspondante, puis cliquez Pages, Supprimer...
Sélectionnez Fenêtre puis Graphe paramètres ou
Choisissez b en abscisse et T en ordonnée sans cocher zéro inclus. Les points expérimentaux esquissent l'allure de la courbe.
Proposez le modèle T=Tmin*(1+b^2/16)
Indiquez dans la case Tmin la valeur de T0 et
(sans Ajuster).
La courbe approchée se trace et coïncide avec les premiers points.
Enregistrez votre fichier : C:\Regressi\documents\votrenom2.rw3
Cliquez Fichier Imprimer: dans la zone paramètres cochez Graphe et modélisation. Imprimez . Sur la feuille commentez et indiquez la limite de validité de la formule approchée (47).

Dans la dernière page graphique vous pouvez également tester une modélisation par équation différentielle.

Proposez: q''= -(2*p/T0)^2*sin(q) et
Régressi connaît déjà T0 (indiqué dans la page Expressions) ne détermine que q'0.
Cette valeur obtenue, retirez le 0 de T0 et modélisez de nouveau.La valeur obtenue pour T doit être très proche de T0.
Cliquez Fichier Imprimer. Dans la zone variables cochez Graphe et modélisation. Imprimez. et commentez.
Enregistrez votre fichier sous: C:\Regressi\documents\votrenom2a.rw3

3.5 Oscillations avec frottement solide

Les frottements solides du potentiomètre sont relativement importants et limitent les possibilités de manipulation avec pendulor. Toujours avec rc = d = 0.45_m, effectuons un enregistrement test.

Dans GTI revenez au calibre 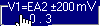pour des oscillations de faible amplitude et vérifiez le zéro
Choisissez une durée de mesure de 10 s et 512 ou même 1024 points
Avec une amplitude initiale proche de 200 mV lancez une acquisition.
Transmettez l'enregistrement à Régressi comme un nouveau Fichier
Dans la page , onglet expressions, ajoutez: q= V1*p/4_rad et T0=......._s , la période mesurée en 3.3 pour les petits angles
Pressez F2 ou mise à jour.
Dans la page Graphique puis affichez q(rad) en fonction de t.
Observez la décroissance linéaire de l'amplitude des oscillations.
Remplacez le curseur standard par le curseur de données. Selectionnez uniquement pente, déterminez la pente de la droite qui joint les maxima successifs. Multipliez mentalement la pente par T0/4 pour évaluer l'ordre de grandeur de qa que vous utiliserez dans la modélisation. Voir paragraphe 2.8 formule (46)
Vous pouvez maintenant proposer une modélisation par une équation différentielle:
q''= - (2*p/T)^2*(q+ qa*sign(q'))
Regressi affecte par défaut la valeur 1 aux paramètres q'0, T et qa
Pour T, tapez la valeur connue de T0 et
Pour qa, tapez la valeur prévue ci dessus
la modélisation devrait réussir....
Enregistrez votre fichier sous: C:\Regressi\documents\votrenom3.rw3
Imprimez un graphe avec le curseur de données et le résultat de la modélisation qui fourni la valeur de qa exprimée par Régressi en milliradians.

On rappelle que l'amplitude décroît de 4 qa par période. Si qa=1.5 mrad par exemple, en 10 périodes l'amplitude a diminué de 60 mrad alors que l'amplitude souhaitable pour des oscillations harmoniques est de l'ordre de 100 mrad. (5,6°)

L'étude de l'amortissement fluide ne peut être abordée que si les frottements solides sont négligeables. Si la valeur obtenue pour qa n'est pas largement inférieure à 1 mrad, le frottement fluide sera totalement masqué. C'est pour cette raison que la manipulation est facultative et reportée en fin de TP.

3.6 Variation de la période en fonction de la position du cylindre

Cette étude est classique pour un pendule pesant. Cependant nous ne pourrons pas traiter les distances inférieures à 20 cm. Les frottements solides du potentiomètre utilisé sont trop importants. Nous effectuerons cependant une série de 16 mesures sur l'intervalle 30cm à 45 cm et pour des tensions juste inférieures à 200 mV (petits angles).

Dans Régressi, chargez le fichier votrenom1.rw3 , auquel vous allez ajouter 15 pages de mesures.

Dans Régressi Windows cliquez sur le bouton
Ajoutez le paramètre expérimental d ; unité m
Dans grandeurs
page 1 donnez la première valeur en mètres :d = 0.45
Dans GTI, fixez de nouveau une durée d'acquisition de 3 s, 512 points
Déplacez le cylindre C à d = 0.44 m, effectuez une acquisition.
Transmettez à Régressi en nouvelle page en indiquant au premier passage dans:
Renseignements page courante:
paramètres d ; unité m ; valeur 0.44
Continuez les acquisitions en incrémentant la valeur d de 0,01 m dans chaque nouvelle page, jusqu'à d = 0. 30 m
sauvegardez votre fichier sousC:\Regressi\documents\votrenom4.rw3
Modélisez ensuite les 16 pages enregistrées avec une fonction sinusoïdale
Dans grandeurs Régressi à ainsi déterminé pour chaque distance d la période T correspondante.
Dans Fenêtres, graphe Paramètres ou
Cliquez et indiquez d en abscisse et T en ordonnée
Un tronçon de courbe apparaît. Laissez l'origine en d = 0 (zéro inclus)

Il convient maintenant de proposer une modélisation en remaniant les formules 31 et 37

Ajoutez une ligne pour calculer I0 , onglet Expressions
Vérifier que I0» Ia + Ib
Dans le graphe paramètres proposez la modélisation suivante:
T(d)=2*p*SQRT((A+Mc*d^2)/G/(Mb*rb-Ma*ra+Mc*d))
Initialement Régressi attribue la valeur 1 aux paramètres A et G.
Aidez Régressi: pour A taper la valeur calculée de I0 et G = 9.81
Ajustez, la modélisation devrait réussir. La courbe extrapolée devrait présenter un minimum pour d = 0.10 m environ
Dans la page Expression, remplacez rc= 0.45_m par rc=d. Pressez F2
Vous disposez ainsi de la courbe théorique T0= f(d)
Enregistrez votre fichier sous: C:\Regressi\documents\votrenom4.rw3
Imprimez en cochant dans la zone paramètres graphe et modélisation (décocher les variables). Commentez

3.7 Oscillations harmoniques amorties (Facultatif)

Le cylindre coulissant est placé à la distance rc = d = 0.45 m. Prenez la grande ailette rectangulaire, notez ses dimensions et son poids. Installez la dans la fente prévue au sommet du pendule.

Avec la formule que vous avez préparée, calculez dans Régressi sa contribution au moment d'inertie total.

Dans GTI.exe revenez à un calibre de ± 200 mV. Allongez à votre convenance la durée d'enregistrement. Ecartez le pendule de 9° environ, lâchez enregistrez et transmettez à Régressi. Modélisez en supposant le frottement fluide. En déduire la valeur de t. Evaluez la valeur de F .

Dans la page expressions de Régressi. Sauvegardez et imprimez graphe et calcul.

Il est évident que ce coefficient caractérise plutôt l'action combinée de l'ailette et du potentiomètre dont on a vu tout au long du TP qu'il introduisait des frottements solides non négligeables. C'est pour cette raison que nous avons évité les termes "frottement fluide" dans le titre du paragraphe.

LIENS

Pour rédiger ce TP j'ai beaucoup consulté les textes de mes collègues

Stéphan Zabroki et Philippe Brizemur. et Jean Michel Millet auteur des logiciels Regressi Windows et Gti.exe.http://perso.wanadoo.fr/jean-michel.millet/

**********************