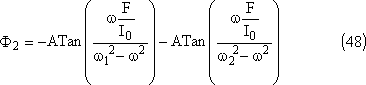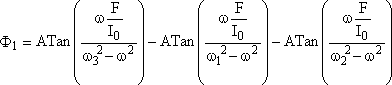Vous montrez dans votre compte rendu que
:![]()
Dans les calculs qui suivent on désignera par :
:![]()
Les équations différentielles du mouvement sont obtenues en appliquant le théorème du moment cinétique à l'instant t :
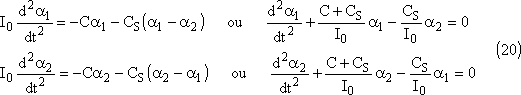
Si le pendule 2 est immobilisé, la première équation différentielle redevient celle d'un pendule simple:
![]()
Il en est de même pour le pendule 2 si on immobilise le pendule 1.
Dans le cas général, les équations différentielles
s'écrivent donc:
![]()
Une solution particulière convenant pour ce couple d'équations
est une fonction sinusoïdale de même pulsation pour les deux
mouvements. Soit en utilisant la notation complexe:
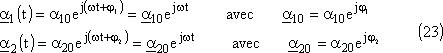
Notons aussi que a10 et a20 sont les amplitudes initiales demandées par Régressi pour la résolution numérique des équations différentielles.
Dans les équations différentielles nous obtenons:
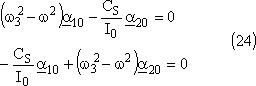
Le déterminant du système doit être nul:
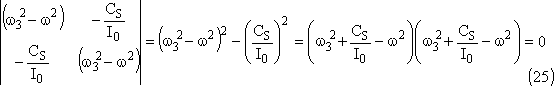
Les pulsations correspondant aux modes propres
sont donc:
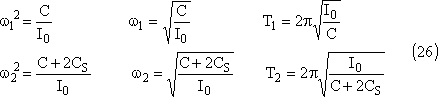
Nous pouvions également développer le déterminant sous
la forme classique de l'équation bicarrée qui fait apparaître
le coefficient de couplage K:
![]()
Les pulsations exprimées comme solutions de l'équation
bicarrée s'écrivent aussi:
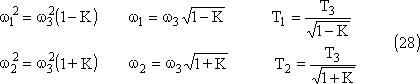
Reportons la valeur de w1 dans l'une
ou l'autre des équations (24).
Nous obtenons: a10 = a20= A. Les deux pendules oscillent en phase.
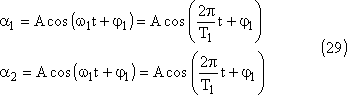
Pour obtenir ce type de mouvement il suffit donc d'écarter dans le
même sens les deux pendules d'un même angle et de les lâcher
simultanément sans vitesse initiale.
Reportons la valeur de w2 dans l'une ou l'autre des équations (24).
Nous obtenons: a10 = -
a20 = B. Les deux pendules oscillent
en opposition phase.
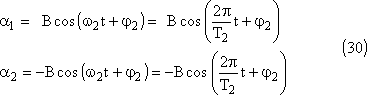
Pour obtenir ce type de mouvement il suffit donc d'écarter les deux
pendules d'un même angle, mais en sens opposés et de les
lâcher simultanément sans vitesse initiale.
Pour un mouvement plus général nous proposerons une combinaison
linéaire des solutions particulières:
![]()
Prenons un exemple de mouvement avec battements qui sera testé en TP.
Le pendule 2 est maintenu à sa position de repos tandis que le pendule
1 est écarté d'un angle
a0. Les deux pendules sont ensuite
libérés sans vitesse initiale à l'instant t=0
![]()
qui conduisent à:
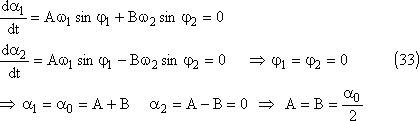
Le mouvement des pendules sera donc représenté par les
équations suivantes:
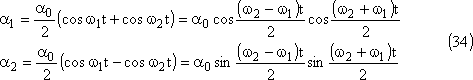
Nous obtenons des battements dont la pulsation de modulation sera notée
wM
![]()
Le mouvement imposé par le moteur à l'extrémité
du ressort de constante de torsion C sera de la forme :
![]()
L'équation différentielle pour le pendule 1 devient donc:
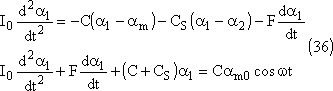
Ecrivons les deux équations différentielles:
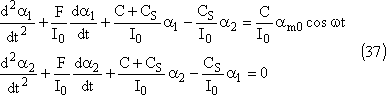
Lorsque le second membre de la première équation est nul on
obtient le régime transitoire:
Posons q = a1 + a2 et y = a1 - a2
En additionnant puis en retranchant les équations différentielles:
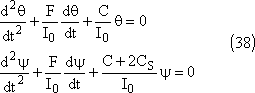
Comme en 2.1.3 , les équations différentielles peuvent
s'écrire:
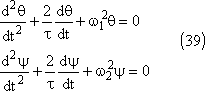
Comme l'amortissement est faible, les solutions sont:
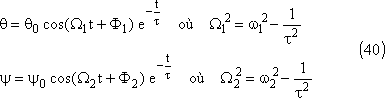
En revenant aux variables initiales la solution générale de
l'équation différentielle avec second membre nul sera:
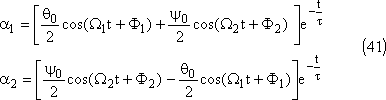
Après démarrage du moteur, le régime transitoire
disparaît rapidement (t> 5t), seuls
subsistent des mouvements sinusoïdaux de pulsation
w:
![]()
Utilisons la notation complexe,
a1(t)
a2(t) et
am(t) sont les parties réelles
de :
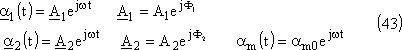
Dans les équations différentielles (37) nous obtenons :
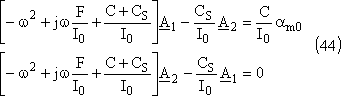
On obtient aisément l'amplitude complexe du mouvement du disque 2:
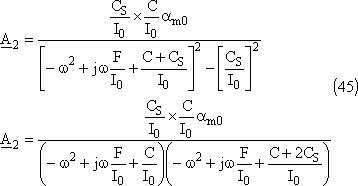
Puis celles des deux disques:
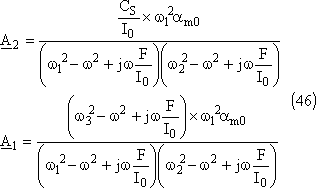
Exprimons les modules des amplitudes:
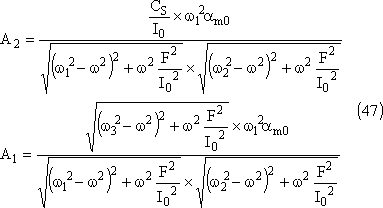
Comme dans le cas du pendule simple, les maxima et le minimum ne sont pas
obtenus exactement pour w =
w1 ;
w2 ou
w3, mais pour des valeurs proches si
l'amortissement est faible. Nous tracerons en TP la courbe expérimentale
de l'amplitude A1 en fonction de la pulsation imposée. Les positions
des maxima et du minimum ne seront que des indications pour aider Régressi
Windows au cours de la modèlisation.