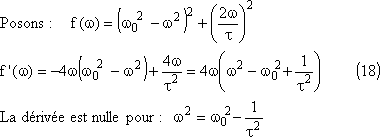Dans les calculs qui suivent on désignera par :
L'équation différentielle du mouvement est obtenue en appliquant le théorème du moment cinétique à l'instant t :
![]()
La solution générale est :
![]()
Pour préparer votre TP évaluez le moment d'inertie
ID du disque d'aluminium de rayon R et d'épaisseur
eD dont la valeur numérique devrait être proche de
I0.
![]()
Effectuez cette application numérique dans la page expression de Régressi Windows en mode simulation.
Les caractères grecs sont obtenus par la combinaison Ctrl r pour r ou Ctrl p pour p
R=75E-3_m
r=2700_kg/m3
eD=10E-3_m
ID=p*r*R^4*eD/2
Régressi donnera le résultat avec l'unité correspondante à la suite de l'expression de ID.
Lancement virtuel de Régressi
Lancement réel de Régressi
Soit IS le moment d'inertie des surcharges par rapport à l'axe de rotation.
La nouvelle pulsation et la nouvelle période seront donc respectivement
:
![]()
Avec les valeurs mesurées de TS et de T0 nous pourrons calculer I0 et Cp
![]()
Vous devrez donc connaître IS aussi précisément que possible.
Les surcharges ou masselottes sont des cylindres d'aluminium de diamètre F, d'épaisseur h. dont les axes de révolution sont situés à la distance r de l'axe de rotation du disque. Vous démontrerez dans votre compte rendu que le moment d'inertie des deux masselottes est :
![]()
Pour chaque masselotte on a les données suivantes :
Pour vous familiariser avec la syntaxe de Régressi Windows, vous effectuerez l'application numérique dans la page expression de Régressi Windows.
'l'apostrophe signale un commentaire
'le caractère souligné précède l'unité
'le caractère F est obtenu par Ctrl Maj
f
m=58.465E-3_kg
Dm=0.05E-3_kg
r=54.94E-3_m
Dr=0.05E-3_m
F=39.45E-3_m
DF=0.05E-3_m
Is=m*(F^2/4+2*r^2)
Régressi donnera directement le résultat numérique avec l'unité correspondante à la suite de l'expression de Is. Vous n'aurez donc pas à utiliser votre calculatrice. Avec la même syntaxe, préparez l'expression de DIs. Régressi Windows calculera également la valeur numérique correspondante en indiquant l'unité.
Lancement virtuel de Régressi Lancement réel de Régressi
Préparez également les expressions donnant l'erreur sur I0 et Cp en utilisant les formules (4). Vous les transcrirez dans la page expression de Régressi pour effectuer l'application numérique avec les valeurs obtenues ci dessus et par modélisation.
2.1.3 Oscillations amorties (frottement fluide faible)
Soit F le coefficient qui caractérise l'amortissement fluide proportionnel à la vitesse.
L'équation différentielle du mouvement devient :
![]()
![]()
Le coefficient F est suffisamment faible pour que la solution soit de la forme :
![]()
La modélisation avec Régressi donnera très facilement la constante de temps t.
Connaissant I0 nous pourrons donc évaluer la valeur de F :
![]()
La valeur de la constante de temps t peut également être obtenue avec le décrément logarithmique D, en mesurant le rapport des amplitudes aux instants t et t + Ta :
![]()
2.1.4 Oscillations forcées avec amortissement visqueux.
Le mouvement imposé par le moteur à l'extrémité
du ressort de constante de torsion C sera:
![]()
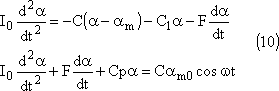
![]()
A la solution générale de l'équation avec second membre
nul (7) s'ajoute une solution particulière de l'équation
complète (11) :
![]()
où w est imposée par le moteur.
Le premier terme s'estompe progressivement.
![]()
Il ne subsiste plus de visible que le régime permanent.
![]()
Utilisons la notation complexe puisque a(t) et am(t) sont les parties réelles de :
![]()
![]()
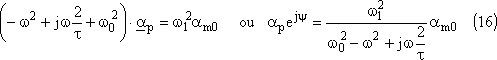
On en déduit l'amplitude
ap et la phase
y:
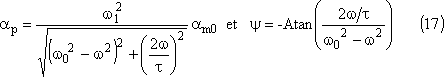
Avec la syntaxe de régressi, nous écrirons (§ 2.2.5) la première expression sous la forme:
b( w) =
A/abs(w0^2- w^2+
j*w*B)
abs(a+jb) signifie module du nombre complexe a+jb
Remarque: le maximum d'amplitude n'est pas obtenu exactement pour
w= w0 mais pour une
valeur un peu inférieure: