Outils de calcul pour Sciences Physiques
Plan
0. Calcul des dérivées
1. Développements en série de puissance
2. Calcul des expressions indéterminées
3. Calcul différentiel
4. Différentielles d’ordre supérieur
5. Différentielles des fonctions de plusieurs variables
indépendantes
6. Calcul intégral
7. Equations différentielles
8. Les différents repères
9. Eléments d'analyse vectorielle
10. Analyse de Fourier
Note de l'auteur
Il ne s'agit pas d'un cours de Mathématiques mais simplement d'un
document pratique pour aider l'étudiant dans les développements
de calcul liés aux apprentissages de la Physique.
Rappel : soit une fonction ![]() ;
on appelle dérivée de
;
on appelle dérivée de ![]() la
quantité égale à
la
quantité égale à ![]() .
.
Nous constatons que les étudiants connaissent les règles de dérivation et les dérivées usuelles. Nous regrettons leur manque de pratique qui leur fait commettre trop d'erreurs si la fonction à dériver "se complique".
1. Développements en série de puissance
Parfois, certains étudiants connaissent quelques développements en série de puissance, rares sont ceux qui savent comment calculer ces développements.
Soit une fonction ![]() définie pour des intervalles de variation de x où elle
ne devient pas infinie et où les dérivées existent.
définie pour des intervalles de variation de x où elle
ne devient pas infinie et où les dérivées existent.
Théorème des accroissements finis : Pour une telle fonction, il existe toujours une abscisse c comprise entre a et b telle que :
![]()
Formule de Mac-Laurin
![]()
Formule de Taylor
![]()
Exemples
![]() ;
; ![]()
![]() ;
;
![]()
Remarques :
2. Calcul des expressions indéterminées
Nous sommes surpris de constater que peu d'étudiants,
spontanément, aient un réflexe d'attention face à des formes
de type ![]() .
.
Premier moyen : Il suffit de développer le numérateur et le dénominateur en série de Mac-Laurin et de simplifier.
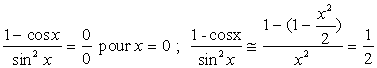
Deuxième moyen. Règle de L’Hopital
![]() se présente sous la forme
se présente sous la forme ![]() ,
alors
,
alors ![]() démonstration
à partir du théorème des accroissements finis.
démonstration
à partir du théorème des accroissements finis.
Par exemple, 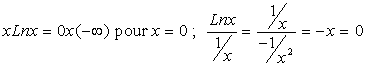
On attribue souvent la paternité du calcul différentiel et intégral à Newton et Leibnitz à la fin du 17ème siècle à la suite d’un grand nombre de travaux mathématiques ayant abouti à l’étude des dérivées, des tangentes aux courbes et des infiniment petits. Ce calcul a été ensuite mis au point par différents mathématiciens (Euler, Laplace, Cauchy, ...) qui lui ont donné sa forme actuelle.
Les infiniment petits. Un infiniment petit est une quantité variable qui tend vers 0.
Exemples,
![]() sont des infiniment petits équivalents si la limite du rapport
sont des infiniment petits équivalents si la limite du rapport ![]() tend
vers 1, quand
tend
vers 1, quand ![]() tendent
vers 0.
tendent
vers 0.
L’infiniment petit ![]() est
équivalent à l’infiniment petit équivalent à x
quand
est
équivalent à l’infiniment petit équivalent à x
quand ![]() alors que
l’infiniment petit
alors que
l’infiniment petit ![]() est
équivalent à
est
équivalent à ![]() .
.
![]() ne sont des infiniment petits équivalents quand
ne sont des infiniment petits équivalents quand ![]() .
.
Les différentielles
La petitesse d’une grandeur est relative. Une minute comparée
à une heure est très petite, mais une minute comparée à
une seconde est très grande.
Dans le calcul différentiel, on appelle dx une très
petite variation algébrique donnée à la variable
x. On peut la prendre aussi petite que l’on veut, mais elle est fixe
et il n’est pas question de la faire tendre vers 0 comme un Dx.
On ne doit pas confondre :
![]() variation algébrique
de x infiniment petite mais non nulle et
variation algébrique
de x infiniment petite mais non nulle et ![]() variation algébrique de x , grande ou petite, que l'on peut faire
tendre vers la valeur nulle.
variation algébrique de x , grande ou petite, que l'on peut faire
tendre vers la valeur nulle.
![]()
En effet, soit par exemple, ![]()
![]() ;
; ![]() ;
;
![]()
Appliquons la formule de Taylor
![]()
![]()
On appelle différentielle de y ou de f(x) la quantité dy = y’dx ou df = f’(x)dx
![]() est une variation algébrique, infiniment petite de
est une variation algébrique, infiniment petite de ![]() qui pourrait être nulle dans le cas particulier d'une fonction
qui pourrait être nulle dans le cas particulier d'une fonction ![]() constante.
constante.
L'introduction de la notion de différentielle permet d'écrire
: ![]()
Calcul des différentielles
Application de la définition : ![]() ;
; ![]()
Différentielles d’une somme, d’un produit, d’un quotient
Soient u et v des fonctions de x.
![]()
![]()
![]()
Différentielles des fonctions de fonctions
Soit y = f(u) avec u = u(x)
![]()
Quelques applications simples des différentielles
![]()
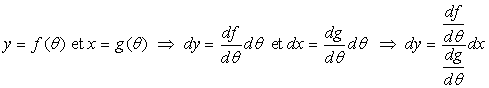
![]()
Exemple : ![]()
4. Différentielles d’ordre supérieur
Nous avons vu que la différentielle de y = f(x) est dy = y’ dx où dx est aussi petit que l’on veut mais fixé.
Nous cherchons la différentielle de dy c’est
à dire d(dy) que nous noterons ![]() (prononciation
" d deux y ").
(prononciation
" d deux y ").
Par définition, ![]() =
(dérivée de dy).dx (dérivée de
dy) = (y’dx)’ = y’’dx
=
(dérivée de dy).dx (dérivée de
dy) = (y’dx)’ = y’’dx
![]()
On aurait de même ![]()
5. Différentielles des fonctions de plusieurs variables indépendantes
En Physique, nous avons souvent à étudier les
fonctions de plusieurs variables indépendantes. Nous limitons à
deux variables indépendantes notées x et y mais
les résultats sont facilement généralisables.
Soit une fonction f(x, y), nous appellerons différentielle de
f (notation df) la quantité ![]() est la dérivée de f par rapport à x, la variable
y étant considérée comme une constante dans la dérivation
(prononciation d rond f sur d rond x).
est la dérivée de f par rapport à x, la variable
y étant considérée comme une constante dans la dérivation
(prononciation d rond f sur d rond x).
La différentielle apparaît comme la somme des différentielles
partielles.
Un grand nombre de mathématiciens prennent a priori cette formule comme
définition de la différentielle et ne la démontrent pas.
Que les esprits ... rigoureux sachent qu’elle se démontre.
L’application de cette formule aux calculs d’erreur est chose importante pour un expérimentateur.
Théorème : soit une fonction de
deux variables f(x, y), on a toujours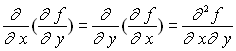
Pour le calcul de la dérivée seconde croisée l’ordre de
dérivation importe peu ; que l’on commence par x et que l’on continue
par y, ou que l’on commence par y et que l’on continue par x,
le résultat est le même.
Remarque importante sur la différentielle d’une fonction
Soit une forme différentielle A(x, y) dx + B(x, y)
dy différentielle d’une fonction f(x, y) c’est à dire
telle que df = A(x, y) dx + B(x, y) dy, alors par définition de
la différentielle d’une fonction f(x, y) nous avons,
![]()
Le théorème sur les dérivées croisées
nous permet d’établir la relation très importante de Cauchy,
![]()
La conséquence de cette relation est simple mais, oh combien importante.
Soit une forme différentielle A(x, y) dx + B(x, y) dy,
On dit que la forme différentielle A(x, y) dx + B(x, y) dy est une différentielle totale exacte.
La forme différentielle A(x, y) dx + B(x, y) dy n’est pas une différentielle totale exacte.
En Physique,
En Thermodynamique, c’est le cas de ce que nous appellons les fonctions d’état : par exemple, la fonction U (énergie interne), ou la fonction H (enthalpie) ou la fonction S (entropie) ou ...
En Thermodynamique, c'est le cas de d W et d Q qui sont des quantités, respectivement de travail et de chaleur, élémentaires (aussi petites que l’on veut) échangées.
Nous devons comprendre d comme l’opérateur mathématique différentiel et d g comme une quantité élémentaire.
Exemples
Il existe une fonction f(x, y) telle que ![]() que nous apprendrons à calculer.
que nous apprendrons à calculer.
Il n’existe pas de fonction g(x, y) et la notation
sera ![]()
Le calcul intégral est l’opération inverse du calcul différentiel à savoir,
La notation pour cette opération est la suivante : ![]() (prononciation somme de ou primitive de f’(x) dx)
(prononciation somme de ou primitive de f’(x) dx)
Nous sommes malheureusement obligés de dire que les
étudiants actuels ne maîtrisent pas le calcul de primitives, pire
que parfois calculer les rebute voire les fatigue.
Pourtant ce qui est demandé au niveau de la Thermodynamique n'est pas
très compliqué et se limite souvent à la connaissances
des primitives élémentaires usuelles.
En cliquant sur le lien Méthodes
d'intégration, l'étudiant trouvera un document dont
nous espérons qu'il lui soit aussi utile qu'il nous fut utile.
Calcul des fonctions f(x, y) dont on connaît la différentielle
![]()
![]() .
Cette primitive est faite en traitant y comme une constante si bien que
la constante d’intégration peut être fonction de y.
.
Cette primitive est faite en traitant y comme une constante si bien que
la constante d’intégration peut être fonction de y.
En reportant le résultat précédent, on
obtient :
![]()
![]()
où il faut bien comprendre que F(x, y) est une primitive par
rapport à x de A(x, y) et que la variable x
s’est éliminée dans ![]() .
.
![]()
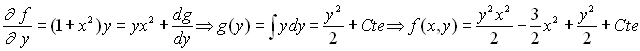
Le lecteur, pour bien comprendre la méthode, aura intérêt
à recommencer le calcul à partir de ![]() .
.
Remarque : Très souvent, en Thermodynamique,
A(x, y) ne sera fonction que de x et B(x, y) que
de y.
Alors ![]()
Le calcul se ramène à celui de deux primitives ordinaires.
Calcul des intégrales curvilignes
On appelle intégrale curviligne l’expression suivante,
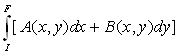 d’un point I
à un point F suivant une courbe d’équation h(x, y) = 0.
d’un point I
à un point F suivant une courbe d’équation h(x, y) = 0.
En Thermodynamique, on dit d’un état initial I à
un état final F suivant une transformation.
Le calcul direct se fait en remplaçant y et dy en fonction
de x et de dx à partir de h(x, y) = 0 dans l’intégrale
curviligne et le calcul devient celui d’une intégrale simple.
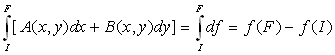 c’est
à dire que le résultat ne dépend pas de la courbe, il ne
dépend que des points I et F (en Thermodynamique, nous dirons que le
résultat ne dépend pas de la transformation et qu’il ne dépend
que des états initial et final).
c’est
à dire que le résultat ne dépend pas de la courbe, il ne
dépend que des points I et F (en Thermodynamique, nous dirons que le
résultat ne dépend pas de la transformation et qu’il ne dépend
que des états initial et final).
Dans ce cas, nous disposons de deux méthodes pour calculer l’intégrale
curviligne.
On appelle équation différentielle une
relation de type ![]() .
D'une manière générale, on ne connaît que très
peu de solutions analytiques des équations différentielles.
.
D'une manière générale, on ne connaît que très
peu de solutions analytiques des équations différentielles.
L'ordre d'une équation différentielle est l'ordre de la dérivée
la plus élevée.
Le Physicien a souvent besoin de trouver les solutions d'équations différentielles dès les premiers semestres de l'enseignement supérieur, or généralement les Professeurs de Mathématiques n'enseignent pas les équations différentielles avant le 4ème semestre. Nous présentons ci-après, de manière pratique, ce qu'il est nécessaire de savoir.
Equations différentielles du premier ordre
Exemple : ![]() ð
ð ![]() ð
ð ![]()
L'intégration d'une équation différentielle du première ordre fait apparaître une constante d'intégration que l'on calcule en Physique à partir d'une condition limite
![]() ð
ð
![]()
La recherche d'une solution particulière est parfois
immédiate. En particulier si ![]() et
et ![]() sont des
constantes, on trouve
sont des
constantes, on trouve ![]() .
.
A défaut, on peut employer la méthode dite
de la " variation de la constante " où dans la solution générale
sans le second membre on pose ![]() ð
ð
![]() .
.
![]()
En remplaçant dans l'équation différentielle,
on obtient ![]()
Le calcul de K(x) se ramène à un calcul de primitive.
Exemple : ![]()
Solution générale sans le second membre : ![]() ð
ð ![]() ð
ð ![]() ð
ð ![]()
Solution particulière :
on remplace dans l'équation différentielle
ð ![]() ð
ð ![]() ð
ð ![]() ð
ð ![]()
La constante K (ou C) est à déterminer à partir d'une condition limite
Equations différentielles du second ordre
Nous limitons nos propos aux équations différentielles
du second ordre linéaires à coefficients constants avec second
membre, soit ![]() .
.
La linéarité entraîne ![]()
On cherche respectivement, pour la solution particulière,
une constante, un polynôme de degré +2 en puissance de x,
une combinaison linéaire de cosinus et sinus du groupement ![]() .
.
En remplaçant, on forme l'équation caractéristique
![]() qui a deux solutions
qui a deux solutions
![]() et
et ![]() .
La solution s'écrit alors
.
La solution s'écrit alors ![]() .
.
En explicitant suivant les valeurs de ![]() ,
,
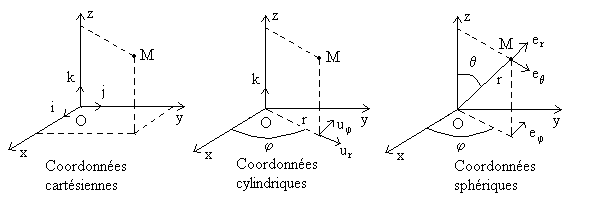
8.1. Repère cartésien
![]() ;
;
![]() ;
; ![]()
8.2. Repère cylindrique
![]() ;
;
![]() ;
; ![]()
8.3. Repère sphérique
![]() ;
;
![]()
8.4. Repère curviligne ou de Frénet
|
|
C : centre du cercle tangent en M à la trajectoire
s : abscisse curviligne
|
9. Eléments d'analyse vectorielle
Prérequis : le produit scalaire, le produit vectoriel.
Produit mixte : ![]()
Double produit vectoriel : ![]()
Opérateur gradient
Soit une fonction f(x, y, z) c’est à dire une fonction des trois variables cartésiennes x, y et z.
Par définition  où
où ![]() sont
les vecteurs unitaires de la base cartésienne habituelle (prononciation
: gradient de la fonction f au point M(x, y, z)).
sont
les vecteurs unitaires de la base cartésienne habituelle (prononciation
: gradient de la fonction f au point M(x, y, z)).
Propriété
Soient ![]() le vecteur position et
le vecteur position et ![]()
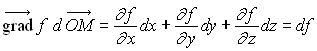
Coordonnées cylindriques : 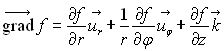
Coordonnées sphériques : 
Opérateur divergence
Soit un vecteur ![]() où les composantes sont des fonctions des variables x, y
et z.
où les composantes sont des fonctions des variables x, y
et z.
Par définition 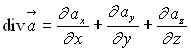
Coordonnées cylindriques : 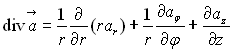
Coordonnées sphériques : 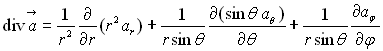
Opérateur Laplacien
Soit une fonction f(x, y, z) c’est à dire une fonction de trois variables indépendantes x, y et z.
Par définition 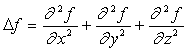 Propriété :
Propriété : ![]()
Coordonnées cylindriques : 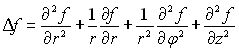
Coordonnées sphériques : 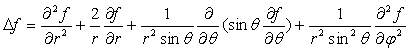
Opérateur rotationnel
Par définition 
Coordonnées cylindriques : 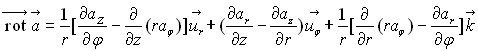
Coordonnées sphériques : 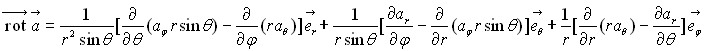
Remarque : tous ces opérateurs sont linéaires
L'opérateur " nabla "
Par définition ![]()
Ainsi, ![]() ,
,
![]() ,
, ![]()
Quelques relations
![]()
![]() ;
; ![]()
![]()
![]()
Théorème d'Ostrogradsky :
![]() ; S
est la surface fermée contenant le volume
; S
est la surface fermée contenant le volume ![]() ;
;
![]() est orienté
vers l’extérieur de la surface fermée S.
est orienté
vers l’extérieur de la surface fermée S.
Théorème de Stokes :
![]() ; la surface
S est quelconque s’appuyant sur le contour
; la surface
S est quelconque s’appuyant sur le contour ![]() ;
;
![]() est orienté
suivant la règle dite du " tire-bouchon " par rapport
au sens de parcours de
est orienté
suivant la règle dite du " tire-bouchon " par rapport
au sens de parcours de ![]() .
.
Formules du gradient : ![]() ;
;
![]()
Formule du rotationnel : ![]()
Formules de Green : ![]() ;
;
![]()
10.1. Série de Fourier
Soit ![]() fonction
réelle ou complexe de la variable réelle t, périodique
de période
fonction
réelle ou complexe de la variable réelle t, périodique
de période ![]() ,
présentant sur l’intervalle
,
présentant sur l’intervalle ![]() un nombre fini de discontinuités, de maxima et de minima, et telle que
un nombre fini de discontinuités, de maxima et de minima, et telle que
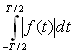 ait une valeur
finie.
ait une valeur
finie.
On peut décomposer ![]() en série de Fourier, c’est à dire écrire
en série de Fourier, c’est à dire écrire ![]() sous
la forme :
sous
la forme : ![]()
avec :  ;
;
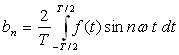 ; la formule
donnant
; la formule
donnant ![]() est valable
pour
est valable
pour ![]() soit
soit 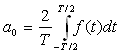
Le terme ![]() correspond au fondamental, les autres termes sont appelés harmoniques.
correspond au fondamental, les autres termes sont appelés harmoniques.
L’importance relative des différents harmoniques est
déterminée par ![]() .
.
Sous forme complexe, les formules ci-dessus peuvent s’écrire :
![]() avec
avec 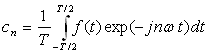
Théorème de Parseval
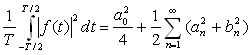 ;
;
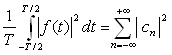
10.2. Transformée de Fourier
Soit ![]() fonction
réelle ou complexe de la variable réelle t ; la fonction
fonction
réelle ou complexe de la variable réelle t ; la fonction
![]() est supposée
de carré sommable, c’est à dire que
est supposée
de carré sommable, c’est à dire que 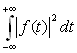 a une valeur finie.
a une valeur finie.
On montre que ![]() peut
s’écrire sous la forme :
peut
s’écrire sous la forme :
 avec
avec 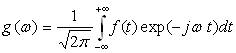
La fonction ![]() est la transformée de Fourier de la fonction
est la transformée de Fourier de la fonction ![]() .
.
Ces formules montrent que la représentation d’une fonction
par superposition de fonction sinusoïdales n’est pas limitée aux
fonctions périodiques.
Une mention particulière doit être faite pour des fonctions périodiques
ou pseudo-périodiques de pulsation ![]() sur une durée
sur une durée ![]() .
.
Le spectre de Fourier ![]() de telles fonctions correspond à un ensemble de sinusoïdes dont
les pulsations appartiennent principalement à l’intervalle
de telles fonctions correspond à un ensemble de sinusoïdes dont
les pulsations appartiennent principalement à l’intervalle ![]() avec
avec ![]() .
.
Ainsi le seul fait de limiter dans le temps une sinusoïde élargit
le spectre de fréquences. Ce résultat surprend, mais il constitue
un des aspects fondamentaux de la transformée de Fourier.