Physique quantique
1. Introduction
1.1. Les faits expérimentaux conduisant à
la Physique quantique
La nature, corpusculaire ou ondulatoire, de la lumière est discutée
depuis longtemps.
Entre la fin du 17ème siècle et jusqu’au milieu
du 19ème siècle, les expériences d’interférences
lumineuses et de diffraction de la lumière ont permis le développement
des théories ondulatoires.
A partir du début du 20ème siècle, des
faits expérimentaux, tels que :
-
l’effet Compton (collision élastique lumière-matière),
-
le rayonnement du corps noir (variation avec la longueur d’onde
du flux lumineux émis par les corps),
-
l’effet photoélectrique (extraction des électrons
d’un métal par une onde électromagnétique),
-
les spectres de raies (émission de lumière par les
atomes gazeux et, en particulier, par l’atome d’Hydrogène),
-
l’expérience de Franck et Hertz (pertes d’énergie
subies par des électrons accélérés à
la suite de collisions avec les atomes d’un gaz),
mettent en évidence le caractère corpusculaire de la lumière.
1.2. Onde associée à une particule
1.2.1. Les idées de L. De Broglie
L’effet Compton, la théorie du rayonnement du corps
noir, l’effet photoélectrique associent à l’onde électromagnétique
une corpuscule appelée photon.
La théorie du corps noir
introduit les notions de quantification de l’énergie et les nombres entiers
en Physique.
L’interprétation des spectres de raies quantifie l’énergie
de la particule électron émettrice d’onde électromagnétique
par changement de niveau d’énergie.
- La première idée de De Broglie est d’étendre le double
aspect onde-corpuscule à toute particule.
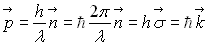 ;
;
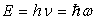
L’onde monochromatique
plane associée à toute particule s’écrit : 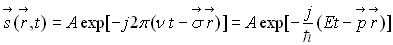
- La deuxième idée s’appuie sur cette constatation : les
nombres entiers apparaîssent en Optique ondulatoire (interférences
et diffraction) et l’Optique géométrique est une approximation
de l’Optique ondulatoire lorsque
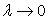 (c’est à dire lorsque la longueur d’onde est faible devant les dimensions
de l’espace dans lequel elle se propage).
(c’est à dire lorsque la longueur d’onde est faible devant les dimensions
de l’espace dans lequel elle se propage).
Il doit en être de même en Mécanique :
la Mécanique newtonienne ou relativiste est une approximation d’une
Mécanique ondulatoire (à construire) si la longueur d’onde associée
à la particule est négligeable.
1.2.2. Ordres de grandeurs de longueurs d’ondes associées
Balle de fusil : 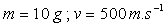 ð
ð 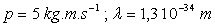
Proton dans un cyclosynchroton de rayon 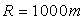 pour
pour 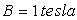 :
: 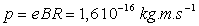 ;
;
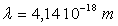
Electron accéléré par une tension U :
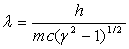 avec
avec 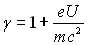
|
U en volts
|
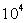
|
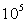
|
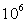
|
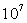
|
|
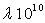 en mètre
en mètre
|
0,12
|
0,037
|
0,0087
|
0,0012
|
Atome : dans la théorie de l’atome de Bohr
(qui donne d’excellents résultats dans l’interprétation des spectres
de raies de l’Hydrogène), la longueur d’onde associée à
l’électron " tournant uniformément autour du proton "
de l’atome d’Hydrogène est égale à 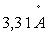 alors que le rayon orbital est égal à
alors que le rayon orbital est égal à 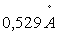 .
.
La théorie de l’atome de Bohr (qui donne d’excellents résultats)
n’a pas grand sens : il convient de considérer l’aspect ondulatoire
de l’électron dans l’atome d’Hydrogène.
1.2.3. Preuves expérimentales directes du bien fondé des idées
de De Broglie
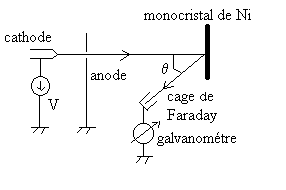
Expérience de Davisson et Germer (diffraction d’électrons)
Le faisceau d’électrons émis par la cathode est
accéléré par la différence de potentiel V
de telle sorte que 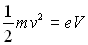 .
.
Les électrons se réfléchissent sur le cristal de Nickel
dans des directions privilégiées (maximum de courant mesuré
par le galvanomètre) telles que 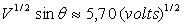 .
.
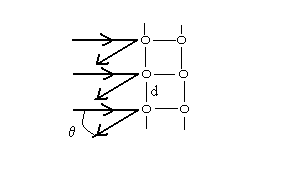
L’interprétation théorique de ce résultat expérimental
admet que les directions privilégiées correspondent à des
différences de phase entre deux ondes successives associées au
faisceau d’électrons et réfléchies sur les atomes du monocristal
de Nickel multiples entiers de 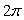 .
.
ð 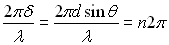 .
.
En utilisant 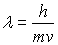 ,
on obtient
,
on obtient 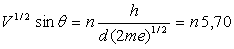 pour
la maille du réseau cristallin de Nickel (
pour
la maille du réseau cristallin de Nickel (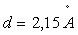 ).
).
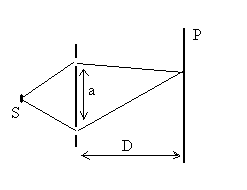
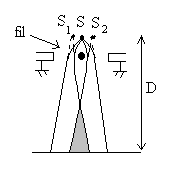
Expérience de Möllenstedt (interférences d’électrons)
Le nombre de franges observées est limité par
l’étendue de la source primaire S (cohérence spatiale)
1.3. Mécanique ondulatoire. Propriétés
de la fonction d’onde
|
|
L’intensité lumineuse est égale à :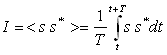
Dans l’expérience des trous d’Young (en ne considérant
pas la diffraction),
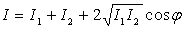 où où
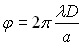
|
Interprétation corpusculaire
La source S émet des photons que l’on détecte
dans le plan d’observation P, après avoir traversé les
trous. Nous cherchons à savoir ce qui s’est passé dans le plan
des trous en réduisant l’intensité lumineuse de telle sorte qu’entre
S et P, à tout instant, il n’y ait qu’un seul photon.
Si l’on place en P une plaque photographique, pendant une faible durée
T, on observe, après développement, des points d’impact
discrets attribués aux photons émis pendant la durée de
l’expérience.
Ces points d’impact se répartissent conformément au résultat
prévu par la théorie ondulatoire, d’où l’idée de
donner à la fonction d’onde lumineuse une signification probabiliste.
Dans un volume 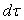 entourant le point
entourant le point 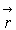 ,
la probabilité de trouver le photon à l’instant t est
,
la probabilité de trouver le photon à l’instant t est
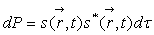 .
.
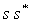 représente alors la densité de probabilité de présence
au point considéré.
représente alors la densité de probabilité de présence
au point considéré.
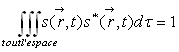 évidemment (condition de normalisation).
évidemment (condition de normalisation).
A la frontière de deux régions, il doit y avoir
continuité de la fonction d’onde et de sa dérivée.
Probabilisme et déterminisme
Dans le déterminisme, le monde et ses objets existent
indépendamment de l’observation. Ainsi dans l’expérience des trous
d’Young, réalisée avec des électrons, le déterminisme
consiste à penser que l’électron est passé par l’un des
deux trous et cela sans observation réelle de ce passage.
Dans l’interprétation probabiliste, l’électron devient particule
si on observe effectivement son passage.
Dans l’expérience des trous d’Young l’électron est une onde dans
la propagation et devient une particule dans la détection au niveau de
l’observation.
On emploie l’expression quanton pour décrire tout système
se comportant soit comme une onde soit comme une particule.
Cette interprétation probabiliste, connue sous le nom d’interprétation
de Copenhague en raison des origines danoises de N. Bohr, a pu heurter des physiciens
et, en particulier, Einstein.
Des expériences comme celle de J. Bell, au CERN en 1965, et celle de
A. Aspect, à Orsay en 1982, tendent à prouver que l’interprétation
probabiliste est actuellement la seule qui soit rationnelle.
2. Les ondes de matière. L’équation
de Schrödinger
2.1. Paquet d’ondes libres. Vitesse de phase et vitesse
de groupe
La probabilité de l’onde plane monochromatique [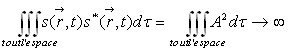 ]
diverge : l’onde monochromatique n’a pas de sens physique dans l’interprétation
probabiliste.
]
diverge : l’onde monochromatique n’a pas de sens physique dans l’interprétation
probabiliste.
Ceci ne peut nous surprendre puisqu’en Optique ondulatoire, la notion d’onde
plane monochromatique a du être abandonnée lorsqu’il a fallu interpréter
des phénomènes interférentiels liés à la
cohérence temporelle.
Nous avons alors introduit l’onde réelle comme une superposition
linéaire d’ondes monochromatiques planes, à savoir
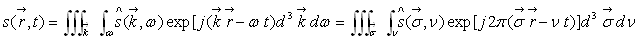 où, par
convention,
où, par
convention, 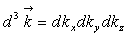 et
et 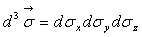 .
.
La technique de la transformée de Fourier permet d’obtenir
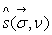 à partir
de
à partir
de 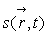 en calculant
une intégrale de forme identique :
en calculant
une intégrale de forme identique :
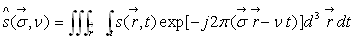 où
où 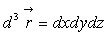
Pour les ondes de matière, les relations ci-dessus
s’écrivent :
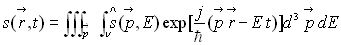 où
où 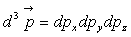
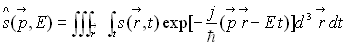
Vitesse de phase : elle est égale à
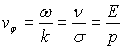
Photon : 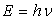 ;
;
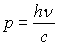 ð
ð
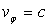
Particule matérielle libre : Mécanique
newtonienne 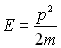 ;
;
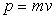 ð
ð
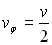
Mécanique relativiste 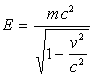 ;
;
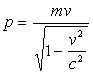 ð
ð
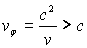
Vitesse de groupe : elle est égale à
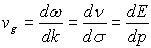
Photon : 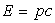 ð
ð 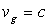
Particule matérielle libre : Mécanique
newtonienne 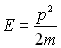 ;
;
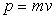 ð
ð
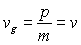
Mécanique relativiste 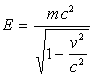 ;
;
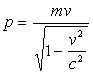 ;
; 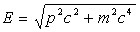 ð
ð 
On rappelle que la vitesse de groupe s’interprète comme
étant la vitesse de déplacement de l’énergie ; pour
une particule, elle s’identifie à sa vitesse.
2.2. Inégalités d’Heisenberg
Inégalité spatiale
|
|
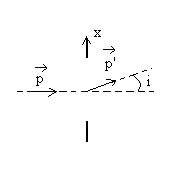
Pour mesurer la position x d’une particule, on
la fait passer à travers une fente de largeur 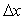 et on la recueille sur un détecteur au-delà.
et on la recueille sur un détecteur au-delà.
Le phénomène de diffraction fait qu’après la fente,
la particule se situe dans un angle maximal 2i tel que 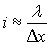 . .
En raisonnant sur les quantités de mouvement,
on peut écrire 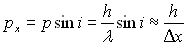 . .
|
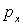 est la quantité de mouvement maximale acquise dans le franchissement
de la fente. Elle est d’autant plus importante que la fente est fine, que l’on
mesure la position de la particule suivant x de manière précise.
Ainsi, vouloir mesurer la position d’une particule introduit nécessairement
une imprécision sur la quantité de mouvement.
est la quantité de mouvement maximale acquise dans le franchissement
de la fente. Elle est d’autant plus importante que la fente est fine, que l’on
mesure la position de la particule suivant x de manière précise.
Ainsi, vouloir mesurer la position d’une particule introduit nécessairement
une imprécision sur la quantité de mouvement.
La généralisation de la relation 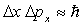 est appelée inégalité (ou incertitude) spatiale
d’Heisenberg.
est appelée inégalité (ou incertitude) spatiale
d’Heisenberg.
On dit que quantité de mouvement et position sont des
quantités conjuguées.
Inégalité temporelle
L’étude de l’Optique ondulatoire montre que l’onde réelle
est nécessairement la superposition d’ondes monochromatiques dont les
fréquences sont comprises entre [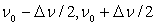 ].
Un calcul simplifié montre que la largeur spectrale
].
Un calcul simplifié montre que la largeur spectrale 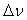 est liée à la durée d’émission
est liée à la durée d’émission 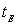 de la source par la relation
de la source par la relation 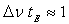 (soit
(soit 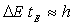 ) . Ainsi
un signal bref occupe une large bande de fréquences contrairement à
un signal long.
) . Ainsi
un signal bref occupe une large bande de fréquences contrairement à
un signal long.
En une position fixée de l’espace, la durée de passage de l’onde
va être égale à 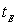 et le temps nécessaire
et le temps nécessaire 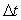 pour mesurer la fréquence (ou l’énergie) de l’onde est au maximum
égal à
pour mesurer la fréquence (ou l’énergie) de l’onde est au maximum
égal à 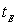 .
.
Nous obtenons la relation 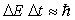 dont la généralisation est appelée inégalité
(ou incertitude) temporelle d’Heisenberg.
dont la généralisation est appelée inégalité
(ou incertitude) temporelle d’Heisenberg.
On ne peut espérer mesurer une énergie avec une précision
infinie, sauf s’il s’agissait d’une énergie parfaitement stable que l’on
mesure pendant un temps infini.
On dit que énergie E et temps t sont des quantités
conjuguées.
2.3. Equation de Schrödinger
Nous avons commencé à établir des similitudes
de comportement entre les ondes et la matière. Il y a, toutefois une
différence importante : dans les situations les plus simples, le
nombre de photons varie au cours du temps par absorption ou émission ;
le nombre de particules élémentaires de matière reste constant
sauf dans quelques cas extrêmes (création d’une paire électron-positron
à partir d’un neutron ou annihilation de cette avec émission de
rayonnement).
Nous avons vu que l’intensité, en un point et à un instant donnés,
de l’onde associée à une particule donne sa probabilité
de la trouver en ce point et à cet instant.
Le problème posé est celui de la prédiction : connaissant
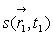 à un endroit
et à un instant, il s’agit de connaître s à tout
endroit et à tout instant.
à un endroit
et à un instant, il s’agit de connaître s à tout
endroit et à tout instant.
Pour cela, il faut connaître l’équation de propagation de
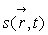 .
.
Comme toute équation de la Physique, sa seule réelle justification
réside dans le succès de la confrontation de ses prédictions
avec les résultats expérimentaux.
2.3.1. Equation de Schrödinger
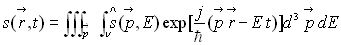
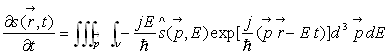
ð 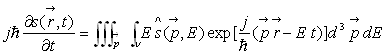
Par la même méthode, on montre que :
Ainsi,
à E est associé l’opérateur 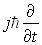
à 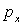 est associé l’opérateur
est associé l’opérateur 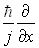
à 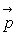 est associé l’opérateur
est associé l’opérateur 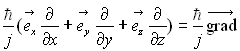
à 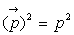 est associé l’opérateur
est associé l’opérateur 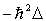
Cas non relativiste d’une particule libre
Elle obéit à 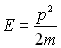 ð
ð 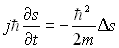
Cas relativiste d’une particule libre
Elle obéit à 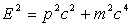 ð
ð 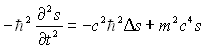 ð
ð 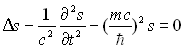
Cas non relativiste d’une particule dans un potentiel scalaire
Elle obéit à 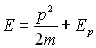 ð
ð 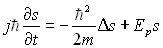
2.3.2. Etats stationnaires
On appelle états stationnaires, les états
de la particule pour lesquels l’énergie E est constante. On les
obtient si l’énergie potentielle ne dépend pas du temps.
Pour résoudre l’équation de Schrödinger,
on cherche des solutions à variables séparées.
ð 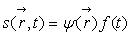 ð
ð 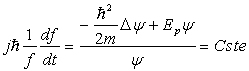 .
.
Cette constante doit être identifiée à E pour vérifier
la dépendance de la fonction d’onde avec le temps.
ð 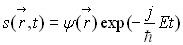 et
et 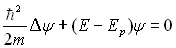 qui est l’équation
différentielle de Schrödinger des états stationnaires.
qui est l’équation
différentielle de Schrödinger des états stationnaires.
La probabilité de trouver la particule dans un élément
de volume 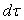 est :
est :
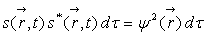
Elle ne dépend
pas du temps, ce qui justifie le qualificatif " stationnaire "
employé.
2.3.3. Etats propres
A une grandeur physique est associé un opérateur.
Dans le cadre de cette représentation d’une grandeur physique par un
opérateur, les états stationnaires apparaissent comme des états
caractérisés par une fonction d’onde particulière.
Ainsi puisque E est constant, 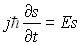 .
.
L’action de l’opérateur " énergie " 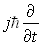 sur la fonction d’onde s se traduit par la multiplication simple de s
par la quantité scalaire E.
sur la fonction d’onde s se traduit par la multiplication simple de s
par la quantité scalaire E.
La fonction d’onde s est une fonction propre et E est la valeur
propre associée.
Ce résultat se généralise à toute grandeur physique
(exemple : 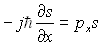 ).
).
Ainsi, toute grandeur physique représentée par un opérateur
est disjointe de ses valeurs numériques qui sont les valeurs propres
de l’opérateur. L’ensemble de ces valeurs forme le spectre de la grandeur.
Ce spectre est toujours discret (quantifié). Toutefois, dans la
plupart des situations courantes, les niveaux d’énergie sont si serrés
que l’on peut considérer que l’ensemble de ces niveaux forme un quasi-continuum,
plus simplement que le spectre d’énergie peut être considéré
comme continu.
Annexe 1 : Les faits expérimentaux
conduisant à la Physique quantique
Effet
Compton (1924) : voir exercices de Relativité
Théorie du rayonnement du corps noir
(1900)
|
|
On expose le raisonnement de Planck où on s ‘intéresse
aux sources du champ électromagnétique (c’est à dire
aux parois de la cavité rayonnante). Une autre démonstration
consiste à considérer les ondes comme une assemblée
de photons obéissant à la statistique de Bose-Einstein.
|
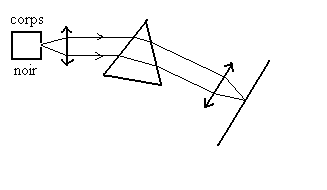
Un corps noir est un corps qui absorbe entièrement le
rayonnement incident constitué de photons d’énergie 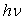 .
Compte tenu da la conservation de l’énergie, il émet pareillement.
Pratiquement, c’est une cavité avec une faible ouverture (tout rayonnement
entrant finit par être absorbé).
.
Compte tenu da la conservation de l’énergie, il émet pareillement.
Pratiquement, c’est une cavité avec une faible ouverture (tout rayonnement
entrant finit par être absorbé).
Les parois sont constitués d’oscillateurs dont chacun a une énergie
 où n
prend toute valeur entière positive à partir de la valeur nulle.
où n
prend toute valeur entière positive à partir de la valeur nulle.
Le
terme 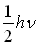 (correspondant
à
(correspondant
à 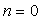 ) n’est
pas évident ; il a été ajouté, pour la première
fois, par Einstein pour mieux vérifier l’expérience. La résolution
de l’équation de Schrödinger pour une énergie potentielle
harmonique montre le bien fondé de cette formule.
) n’est
pas évident ; il a été ajouté, pour la première
fois, par Einstein pour mieux vérifier l’expérience. La résolution
de l’équation de Schrödinger pour une énergie potentielle
harmonique montre le bien fondé de cette formule.
Chaque niveau d’énergie est équiprobable suivant
la fonction de Boltzmann 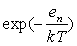 .
.
Soit 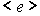 l’énergie moyenne d’un oscillateur.
l’énergie moyenne d’un oscillateur.
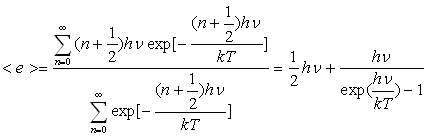
Si 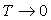 ,
,
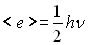 ce qui montre
l’existence d’énergie à température absolue nulle
ce qui montre
l’existence d’énergie à température absolue nulle
Si 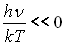 ,
,
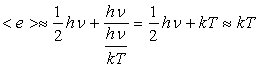
Couramment, 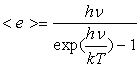
Nous calculons le nombre d’oscillateurs en calculant le nombre
d’ondes dans la cavité. Le flux lumineux, pour une température
donnée, ne dépend pas de la forme de la cavité. Il est
légitime de choisir une forme simple (parallélépipède
rectangle de dimensions 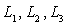 ).
).
Pour cette forme, l’étude des ondes montrent que les relations 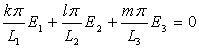 et
et 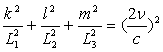 doivent être
vérifiées.
doivent être
vérifiées.
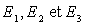 sont les amplitudes
du champ électrique dans les trois directions d’espace (deux seulement
sont indépendantes) ;
sont les amplitudes
du champ électrique dans les trois directions d’espace (deux seulement
sont indépendantes) ; 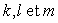 sont entiers positifs.
sont entiers positifs.
Le flux lumineux émis, pour une température donnée, ne
dépend pas de la forme de la cavité.
Pour 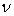 donné,
il y a
donné,
il y a 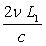 pour k,
pour k,
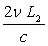 pour l
et
pour l
et 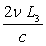 pour m,
soit
pour m,
soit 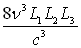 combinaisons
possibles pour
combinaisons
possibles pour 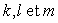 sans tenir compte de la relation
sans tenir compte de la relation 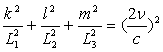 qui peut être comprise dans des axes cartésiens
qui peut être comprise dans des axes cartésiens 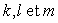 comme l’équation d’un ellipsoïde dont le huitième (
comme l’équation d’un ellipsoïde dont le huitième (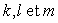 entiers positifs) de volume est égal à
entiers positifs) de volume est égal à 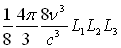 .
.
Le nombre d’ondes (nombre de combinaisons 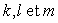 )
de fréquence
)
de fréquence 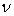 dans une cavité de volume
dans une cavité de volume  est donc
est donc 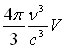 .
.
Le nombre d’ondes de fréquences comprises entre 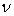 et
et  est égale
à
est égale
à 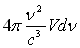 .
.
L’énergie contenue, par unité de volume, pour
des fréquences comprises entre 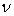 et
et  , est égale puisqu’il
y a deux degrés de liberté à :
, est égale puisqu’il
y a deux degrés de liberté à :
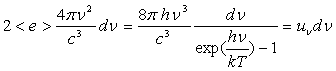 où
où 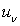 est la densité spectrale volumique d’énergie (cette expression
aurait pu être établie par la statistique de Bose-Einstein).
est la densité spectrale volumique d’énergie (cette expression
aurait pu être établie par la statistique de Bose-Einstein).
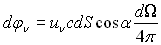 ð
ð 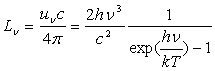 formule qui est bien vérifiée par l’expérience.
formule qui est bien vérifiée par l’expérience.
Le flux lumineux total émis par unité de surface
est égal à : 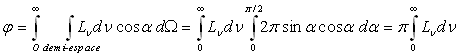
 en posant
en posant 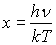
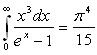 ð
ð 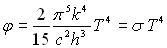 où
où 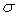 constante
de Stefan-Boltzmann est calculée à
constante
de Stefan-Boltzmann est calculée à 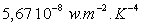 et mesurée à
et mesurée à 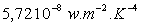 .
.
Effet photoélectrique (1905)
L’interprétation donnée par Einstein fait appel
à la collision inélastique d’un photon sur les électrons
libres du métal constituant la cathode. Le photon est absorbé
par l’électron de telle sorte que 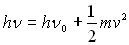 où
où 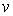 est
la vitesse d’extraction de l’électron.
est
la vitesse d’extraction de l’électron.
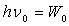 est l’énergie nécessaire à fournir pour extraire un électron
libre du métal.
est l’énergie nécessaire à fournir pour extraire un électron
libre du métal.
Cette énergie s’explique par le fait que, lorsqu’un électron sort
du métal, il est retenu par les charges positives du métal. Cette
énergie d’extraction est faible, toujours inférieure à
l’énergie d’ionisation d’un atome du métal : il s’agit bien
des électrons libres.
Il n’y a pas d’émission secondaire de lumière ce qui prouve qu’il
s’agit de l’absorption du photon incident.
Si 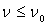 , il n’y a
pas de courant quelque soit le potentiel accélérateur.
, il n’y a
pas de courant quelque soit le potentiel accélérateur.
Si 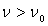 , il est possible
d’arrêter le courant électrique en portant l’anode à un
potentiel négatif
, il est possible
d’arrêter le courant électrique en portant l’anode à un
potentiel négatif 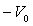 tel que
tel que 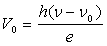 .
.
Pour un potentiel V accélérateur positif augmentant, on
atteint un courant de saturation proportionnel au flux lumineux (au nombre de
photons incidents).
Spectre de raies émis par les atomes
(notamment par l’atome d’Hydrogène)
Le spectre d’émission d’une lampe contenant de l’hydrogène à
une pression de 1 mm de mercure n’est pas un spectre continu mais un
spectre de raies. Les raies du spectre visible correspondent, comme l’a montré
J. Balmer, à des longueurs d’onde 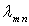 reliées à deux nombres entiers
reliées à deux nombres entiers 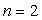 et
et 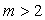 par l’équation :
par l’équation :
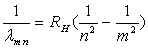 .
.
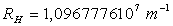 :
constante de Rydberg
:
constante de Rydberg
Interprétation de N. Bohr (1913) à partir du modèle
planétaire de l’atome d’Hydrogène 
Ce modèle n’a plus de sens physique (Bohr, en fin de carrière
refusait de l’enseigner). Le vrai calcul consiste à résoudre l’équation
de Schrödinger pour un potentiel scalaire à symétrie sphérique
en 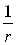 .
.
Ceci étant précisé, le modèle planétaire est
simple et donne un excellent accord avec l’expérience.
Il s’agit du problème à deux corps entre le proton (noyau) et l’électron
en orbite autour dans l’interaction coulombienne.
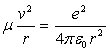 ;
;
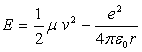 où
où
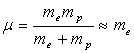 est la masse
réduite introduite pour plus d’exactitude.
est la masse
réduite introduite pour plus d’exactitude.
Les idées de Bohr , en contradiction avec la physique
classique, consiste à dire :
- sur certaines trajectoires privilégiées, l’électron
ne rayonne pas (ces trajectoires sont définies par une quantification
du moment cinétique
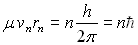 avec
avec 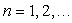 )
)
- l’émission de la lumière doit être attribuée
à des transitions de l’électron d’une trajectoire à une
autre d’énergie plus faible.
En remplaçant, on obtient :
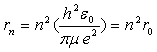 (
(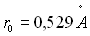 ) ;
) ;
 (
(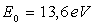 )
)
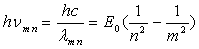 ;
;
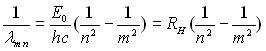
Ces formules sont bien vérifiées par l’expérience
dans le cas de la série des raies de Balmer et, aussi de celles de Lyman
(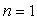 ), de Paschen
(
), de Paschen
(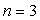 ), de Brackett
(
), de Brackett
(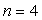 ) ou de Pfund
(
) ou de Pfund
(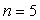 ).
).
Expérience de Franck et Hertz (1914)
L’analyse des pertes en énergie des électrons
fait apparaître des valeurs caractéristiques : dans le cas
de collisions avec des atomes d’une vapeur de mercure, ces pertes sont des multiples
de 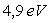 .
.

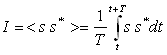
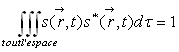 évidemment (condition de normalisation).
évidemment (condition de normalisation).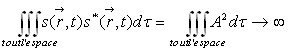 ]
diverge : l’onde monochromatique n’a pas de sens physique dans l’interprétation
probabiliste.
]
diverge : l’onde monochromatique n’a pas de sens physique dans l’interprétation
probabiliste.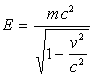 ;
;
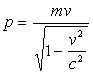 ð
ð

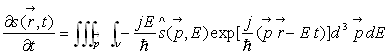
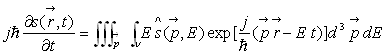
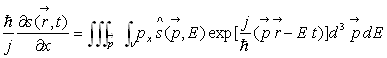
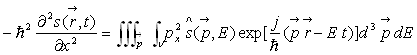
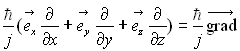
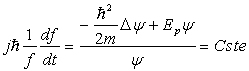 .
.
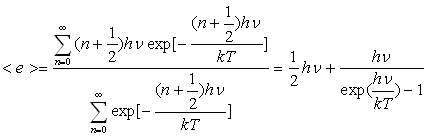
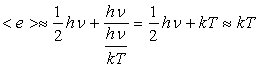
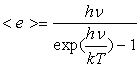
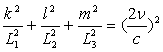 doivent être
vérifiées.
doivent être
vérifiées.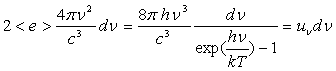 où
où 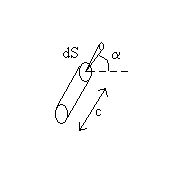
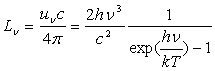 formule qui est bien vérifiée par l’expérience.
formule qui est bien vérifiée par l’expérience.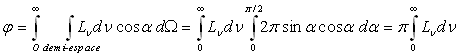
 en posant
en posant 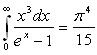 ð
ð 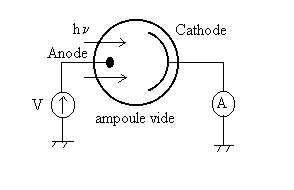
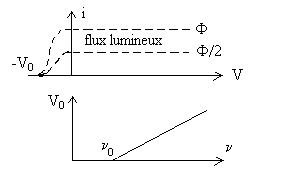
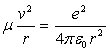 ;
;
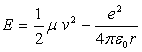 où
où
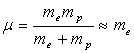 est la masse
réduite introduite pour plus d’exactitude.
est la masse
réduite introduite pour plus d’exactitude.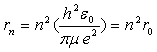 (
( (
(