Ce chapitre est consacré à la réalisation d'un laser compact à sécurité oculaire pompé par diodes laser de puissance dont la partie active est une matrice dopée avec des ions erbium
Les résultats présentés dans ce chapitre n'ont pas été effectués sur le même matériau que celui présenté dans le chapitre 1. En effet, si la matrice est la même, les dopages sont différents. Les dopages utilisés dans ce chapitre ne nous ont pas été communiqués pour des raisons de propriété industrielle par la société Kigre Inc.. Toutefois à la lumière des analyses menées au chapitre 1, nous avons pu les estimer à partir des sections efficaces :
Trois sources de pompage différentes ont été utilisées :
Avec les deux premières sources qui sont des sources continues, deux modes de fonctionnement ont été étudiés :
La troisième source n'est pas une source continue mais une source quasi-continue (voir paragraphe 5.4.1) et seul un mode de fonctionnement en régime relaxé a été étudié.
Le schéma de principe de l'expérimentation est présenté sur la
figure 5-1.
figure 5-1 : Schéma
expérimental.
La longueur d'onde d'émission du laser Ti:Al2O3 est optimisée vers 975 nm. Le point de focalisation du faisceau de pompe est positionné approximativement au milieu du matériau actif.
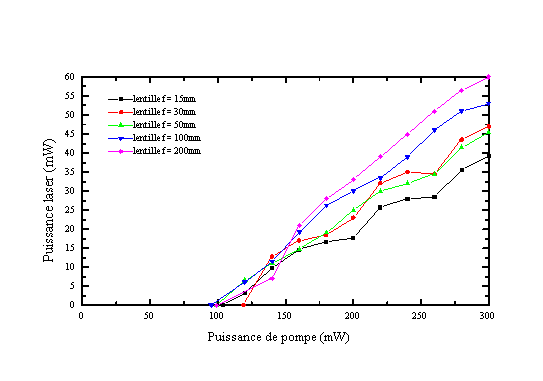
Plusieurs lentilles de focalisation ont été testées (voir figure 5-2) de manière à optimiser la dimension du point de focalisation du faisceau de pompe. Le tableau 5-1 présente un récapitulatif des puissances de pompe au seuil et des rendements pour les différentes lentilles utilisées.
f = 15 mm |
f = 30 mm |
f = 50 mm |
f = 100 mm |
f = 200 mm |
|
Seuil (mW) |
104 |
119 |
99 |
95 |
99 |
Rendement (%) |
19,5 |
23 |
22 |
26,5 |
30 |
Une lentille de focale 400 mm a aussi été essayée mais aucun effet laser n'a été observé.
Le meilleur rendement est donc obtenu pour une lentille de focalisation
de 200 mm, ce qui correspond à un rayon à 
du point de
focalisation d'environ 100 µm. Le faisceau issu du laser Ti:Al2O3
est à peu près collimaté sur une distance d'environ 2 mm, on peut donc estimer la
dimension du point de focalisation après la lentille par la formule : 
avec :
: longueur d'onde du faisceau
f : focale de la lentille
D : diamètre du faisceau collimaté incident.
Une fois la lentille de focalisation optimale déterminée, on refait une série de mesures (voir figure 5-3).
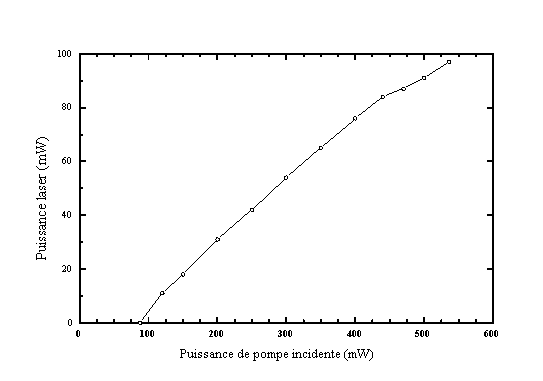
On obtient donc un seuil de 88 mW, une pente de 25% et un rendement optique/optique de 18%. Dans cette configuration la cavité du laser de pompe a été légèrement modifiée de manière à obtenir une puissance de pompe plus importante. Cela se traduit certainement par une modification de la qualité de mode de ce faisceau. Cette modification explique en partie les différences de puissance de pompe au seuil et de rendement différentiel externe entre la figure 5-2 et la figure 5-3.
figure 5-4 : Schéma du
dispositif permettant de mesurer la divergence du faisceau laser.
Le filtre semi-conducteur absorbe le faisceau de pompe. Le détecteur au
germanium monté sur une translation motorisée et muni d'une fente de 100 µm permet
d'enregistrer le profil du faisceau selon deux axes perpendiculaires à l'axe de
propagation. Le diamètre du faisceau est mesuré à différentes positions sur l'axe de
propagation, ce qui permet de calculer la divergence du faisceau selon ces deux axes (voir
figure 5-5).
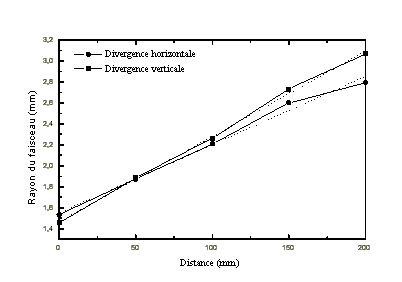
figure 5-5 : Divergence du faisceau laser suivant deux axes perpendiculaires.
En dehors de la zone de Rayleigh, l'accroissement du diamètre du
faisceau est proportionnelle à la distance entre la cavité laser et le détecteur : 
avec
: divergence du faisceau
w : rayon à 
du faisceau.
On a donc une divergence de 8 mrad suivant l'axe horizontal et 6,5 mrad
suivant l'axe vertical.
Le diamètre d'un faisceau gaussien parfait en fonction de la position sur l'axe de propagation est donné par [21] :
avec :
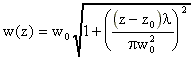
w0 : rayon à 
du faisceau au point
de focalisation,
z0 : position sur l'axe de propagation du point de focalisation du faisceau,
z : position sur l'axe de propagation,
: longueur d'onde du faisceau.
Le paramètre M d'un faisceau qualifie l'écart de divergence entre un
faisceau quelconque et un faisceau unimodal ayant la même taille de mode au point de
focalisation :
|
équation 5-1 |
Si M = 1, alors le faisceau mesuré suit une distribution parfaitement gaussienne. Il
est alors limité par la diffraction.
figure 5-6 : Schéma du
dispositif permettant de mesurer le paramètre M du faisceau.
En focalisant le faisceau en sortie de cavité et en effectuant différentes mesures de part et d'autres du point de focalisation (voir figure 5-7), il est possible de calculer le paramètre M du faisceau laser en optimisant les paramètres de l'équation 5-1 par la méthode des moindres-carrés de manière à faire correspondre les paramètres de cette équation avec les points de mesures.
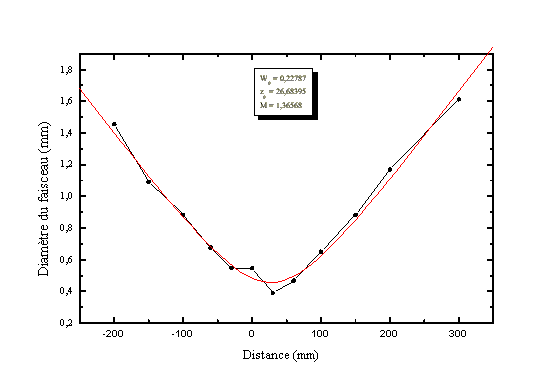
figure 5-7 : Mesure du paramètre M du faisceau.
On obtient donc un paramètre M de 1,3. On peut donc dire que le
faisceau est à peu près limité par la diffraction.
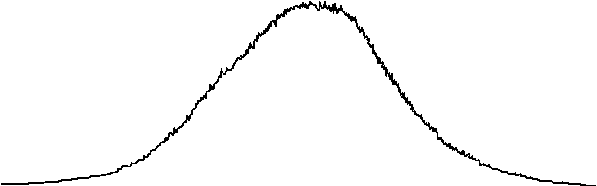
figure 5-8 : Profil spatial du
faisceau laser en champ lointain.
On peut aussi voir sur la figure 5-8 que le profil spatial du faisceau,
à une asymétrie, près est relativement proche d'une gaussienne. Cette asymétrie peut
s'expliquer par une légère asymétrie du faisceau de pompe (voir paragraphe 5.2.1.4). En
effet la cavité utilisée est à miroirs plans parallèles, elle est donc stabilisée par
le guidage par le gain et l'éventuelle lentille thermique. Ces mécanismes sont
engendrés par le faisceau de pompe.
Connaissant la divergence et le paramètre M, il est facile de connaître la dimension du mode intra-cavité. En se plaçant en dehors de la zone de Rayleigh, l'équation 5-1 devient :
avec :
: divergence du faisceau,
: longueur d'onde,
w0 : dimension du mode au point de focalisation.
On a donc la dimension du mode intra-cavité sur l'axe horizontal (w0h
= 78 µm) et vertical (w0v = 97 µm).
La dimension du point de focalisation du faisceau de pompe nous est
nécessaire pour modéliser le fonctionnement du laser.
A partir du schéma de la figure 5-6, on se place au maximum de
puissance de pompe puis on retire le miroir de sortie, les filtres et les densités. On
fait l'image de la face de sortie du matériau actif sur une caméra CCD (voir figure
5-9). On déplace légèrement la lentille de focalisation du faisceau de pompe suivant un
axe perpendiculaire à l'axe de propagation d'une distance connue et on mesure le
déplacement correspondant sur la caméra. Le rapport des deux donne le grandissement :
G=4. On mesure le profil du faisceau à l'aide d'un système d'analyse de profil (voir
figure 5-10). Les rayons mesurés sont ensuite divisés par le grandissement introduit par
la lentille d'imagerie. On obtient donc les dimensions horizontales et verticales du point
de focalisation du faisceau de pompe qui sont respectivement : wph = 96 µm et
wpv = 112 µm.
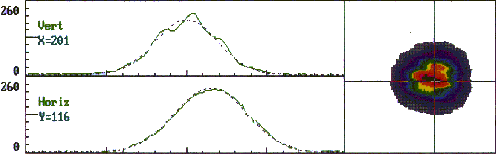
figure 5-10 : Profil spatial
du faisceau de pompe au point de focalisation
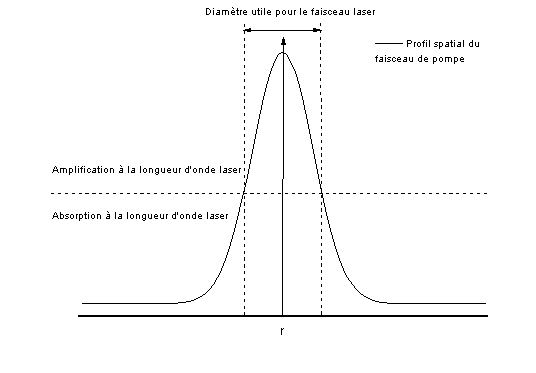
On a donc le profil du faisceau laser qui suit à peu près le profil du faisceau de pompe mais en étant plus petit. Ceci s'explique par le fait que l'ion erbium est décrit par un système de type 3 niveaux, c'est à dire ayant une absorption non-négligeable à la longueur d'onde laser. Le profil du faisceau de pompe crée donc une zone de gain mais ayant une dimension légèrement plus petite que la zone pompée (voir figure 5-11).
Nous allons maintenant présenter ce même laser déclenché par
commutation des pertes.
Le dispositif expérimental est le même que celui présenté sur la figure 5-1. Un disque tournant présentant une ouverture de 1 mm est inséré dans la cavité entre le matériau actif et le miroir de sortie.
On obtient un fonctionnement impulsionnel par commutation des pertes. Le profil temporel de l'impulsion est mesuré à l'aide d'une photodiode InGaAs ayant un temps de réponse de 0,5ns.
Le profil temporel de l'impulsion laser obtenue est présentée figure
5-12. La largeur à mi-hauteur est 48 ns pour une énergie de 8,6 µJ. La puissance crête
associée est donc de 180 W.
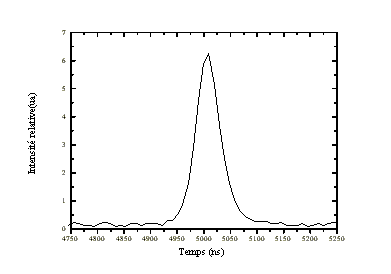
figure 5-12 : Profil temporel
de l'impulsion laser.
A la vue des résultats obtenus en pompage par un laser à saphir dopé
au titane, nous pouvons remplacer le laser de pompe par une diode laser. La puissance de
pompe au seuil devrait être plus importante et le rendement différentiel externe devrait
être plus faible du fait des propriétés spectrales et spatiales de la diode laser
comparées à celles d'un laser à saphir dopé au titane.
La cavité à miroirs plans parallèles est surtout stabilisée par le
guidage par le gain (si les miroirs sont directement en contact avec le matériau actif)
car la lentille thermique est divergente (
selon les données du
fabriquant). La forme du faisceau laser est donc définie par la forme du faisceau de
pompe. L'obtention d'un faisceau monomode transverse étant importante, nous avons
décidé de circulariser le mode de pompe de la diode laser par une fibre optique
multimodale.
Le schéma du dispositif mis en oeuvre est présenté figure 5-13.
figure 5-13 : Schéma du
dispositif de pompage par diode laser de puissance.
La diode laser de puissance est directement couplée dans une fibre
optique multimodale de 125 µm de cœur, de 140 µm de gaine et dont l'ouverture
numérique est 0,48. La sortie de la fibre optique est imagée avec un grandissement de
deux dans le matériau actif par l'intermédiaire de deux lentilles asphériques traitées
antireflet à la longueur d'onde d'émission de la diode laser. Le matériau actif et le
miroir de sortie sont identiques à ceux représentés sur la figure 5-1.
Les diodes laser utilisées dans cette étude sont réalisées au Laboratoire Central de Recherches de Thomson-CSF au sein du Laboratoire Matériaux et Technologies Optoélectroniques.
Ces diodes laser sont ensuite caractérisées en puissance dans notre
laboratoire avant d'être fibrées par Thomson-CSF Semi-conducteurs. Elles sont ensuite
caractérisées dans leur forme définitive.
Le schéma de la structure de la diode laser est présentée sur la
figure 5-14.
figure 5-14 : Schéma de la
structure d'une diode laser de puissance.
La partie active (zone de gain) de la diode (voir figure 5-14) est le puits quantique contraint. La cavité optique est définie par :
La cavité optique a donc à peu près les dimensions suivantes :
Le faisceau émis par la diode devrait donc présenter une
demi-divergence à 
: 
où est la longueur
d'onde émise et w0 la dimension du mode. On obtient donc :
18° 
0,18° Pour comparer ces valeurs avec celles obtenues à partir de la figure 5-16 et de la figure 5-17. Il faut multiplier ces valeurs par 2ln(2) car les valeurs mesurées sont les divergences totales à mi-hauteur :
26° pour 31° mesurés, 
0,26° pour 10° mesurés. La différence existant entre les valeurs théoriques et expérimentales
selon l'axe des x provient de la difficulté à connaître a priori la dimension exacte de
la zone émissive dans cette direction. Par contre la différence entre les valeurs
théoriques et expérimentales de la divergence suivant l'axe des y est due au caractère
non gaussien du faisceau dans cette direction. En effet l'équation reliant la divergence
à la dimension du mode n'est valable que pour un faisceau de profil spatial gaussien. On
caractérise donc la divergence dans cette direction par son écart à la divergence d'un
faisceau gaussien ayant la même dimension de mode : 
. Cet
astigmatisme est dû essentiellement au guidage par le gain du faisceau laser suivant
l'axe y.
La puissance émise par la diode laser en fonction du courant est
présentée figure 5-15.
figure 5-15 : Puissance laser
émise par une diode à 0,98 µm en fonction du courant.
La diode présente un courant de seuil de l'ordre de 250 mA et un rendement différentiel externe de 0,8 W/A. Elle est capable de délivrer une puissance optique de 1,3 W sans présenter de vieillissement sur plusieurs centaines d'heures de fonctionnement.
Les diagrammes de rayonnement en champ lointain dans les plans
perpendiculaires et parallèles à la jonction sont présentés figure 5-16 et figure
5-17.
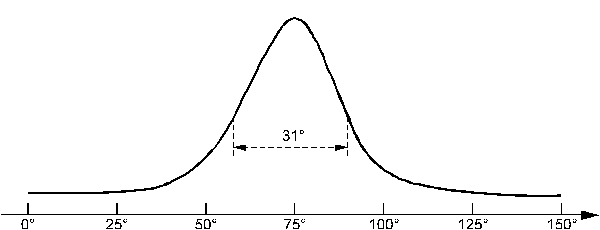
figure 5-16 : Diagramme de
rayonnement de la diode laser dans le plan perpendiculaire à la jonction.
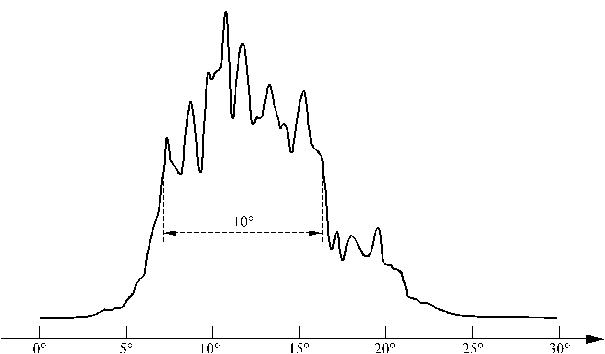
figure 5-17 : Diagramme de
rayonnement de la diode laser dans le plan parallèle à la jonction.
Le faisceau est issu d'une surface de 100*1 µm2, la
divergence dans le plan parallèle à la jonction est 
=10° et
dans le plan perpendiculaire à la jonction est 
=31°.
Pour coupler efficacement le faisceau issu de la diode laser dans une
fibre optique multimodale sans avoir recours à une optique de couplage, il faut utiliser
une fibre dont le diamètre du coeur couvre la surface émissive de la diode laser ( 100
µm) et dont l'ouverture numérique est suffisante pour obtenir un couplage correct. La
fibre optique utilisée est une fibre silice/polymère dont le diamètre de coeur est 125
µm, le diamètre de gaine est 140 µm et l'ouverture numérique est ON = 0,37.
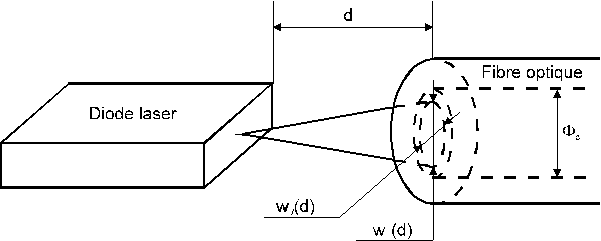
figure 5-18 : Schéma de
principe du couplage d'une diode laser dans une fibre optique multimodale
On considère que la fibre optique est suffisamment proche de la diode
pour que tous les rayons lumineux émis avec une incidence inférieure à 
(ON : ouverture numérique de la fibre) pénètrent dans le coeur de la
fibre. Pour que cette condition soit vérifiée la distance d entre la fibre et la diode
doit être inférieure à dmax.
On obtient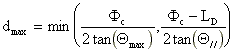 
avec LD=100µm : largeur
du ruban d'émission de la diode. Pour une fibre optique ayant un diamètre de coeur de
125 µm et une ouverture numérique de 0,37, on obtient dmax=140 µm. En
pratique la distance entre la fibre et la diode peut être inférieure à cette valeur
assurant ainsi la validité de cette hypothèse.
Le caractère multimodal du rayonnement émis par la diode n'est pas
pris en compte. L'onde sera supposée à distribution gaussienne TEM00. A une
distance d de la diode, l'intensité 
émise par la diode est
donnée par :
w et w// sont les rayons des
faisceaux à mi-hauteur, 
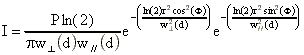
et 
sont
les demi-divergences à mi-hauteur, avec w//(d)= 
,
w (d)=
) et P : puissance émise par la diode.
La puissance couplée dans la fibre est :
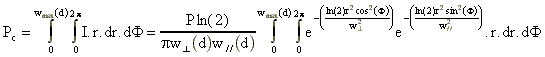
avec wmax (d)=d tan(arcsin(ON)).
Ce calcul ne tient pas compte des pertes par réflexion à l'entrée et à la sortie de la fibre. Pour les modéliser de façon rigoureuse, il faudrait décomposer l'onde émise par la diode en ondes planes et utiliser les formules classiques d'électromagnétisme donnant la transmission en fonction de l'angle d'incidence. Pour des angles d'incidence inférieurs à 30°, ce calcul n'est pas nécessaire car les coefficients de transmission varient peu par rapport à leur valeur en incidence normale (soit pour une fibre ayant un coeur en silice d'indice 1,45, une transmission de 0,96). Le coefficient de couplage total est donc :
.
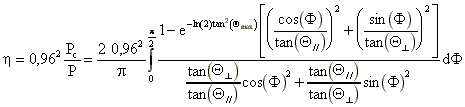
Cette intégrale est calculée numériquement. Pour une diode laser
ayant une largeur de zone émissive de 100 µm , une divergence parallèlement et
perpendiculairement à la jonction valant respectivement 
=10° et 
=31° couplée dans une fibre optique ayant un diamètre de coeur de
125 µm et une ouverture numérique de 0,37, on trouve un couplage théorique de 78%.
La fibre est positionnée en optimisant le couplage puis le support de
fibre est soudé sur le support de diode à l'aide d'un laser YAG ( voir figure 5-19).
figure 5-19 : Diode laser
fibrée
La puissance émise par la diode avant fibrage ainsi que la puissance
disponible en sortie de fibre après fibrage en fonction du courant sont présentées
figure 5-20. On peut donc ainsi évaluer le couplage pour chaque point de mesure. Les
caractéristiques spatiales du faisceau issu de la diode varient en fonction du courant
injecté ce qui explique les légères variations du coefficient de couplage en fonction
du courant.
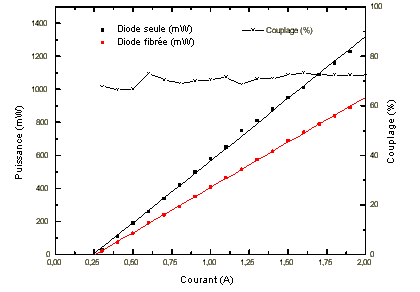
On trouve un couplage moyen de 73 % pour un couplage théorique de 78 %.
La puissance maximale en sortie de fibre est d'environ 0,9 W pour un courant d'injection
de 2 A.
Le spectre d'émission de la diode laser fibrée est présenté figure
5-21.
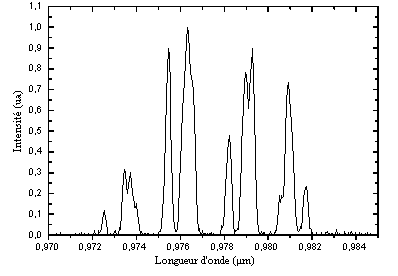
figure 5-21 : Spectre de la diode fibrée à T=26,6 °C (résolution 0,1 nm)
Sa largeur à mi-hauteur est de : 8 nm. Cette largeur spectrale est plus
importante que celle observée habituellement pour les diodes laser (3 nm). De plus le
spectre d'une diode laser est normalement continu et non une succession de pics comme sur
la figure 5-21. Le spectre de la diode laser seule présente les mêmes caractéristiques,
la forme du spectre de la diode laser fibrée n'est donc pas due à la présence de la
fibre optique. La largeur du spectre de la diode étant supérieur à la largeur à
mi-hauteur du spectre d'absorption du matériau (6 nm) l'efficacité du laser pompé avec
cette diode risque de ne pas être optimale.
Nous allons maintenant présenter les deux modes de fonctionnement que nous avons expérimentés avec cette diode laser fibrée comme source de pompage optique :
Le schéma de principe de l'expérimentation est présenté figure 5-13.
La puissance laser émise à 1,5 µm ainsi que le coefficient
d'absorption en fonction de la puissance de pompe sont présentés figure 5-22.
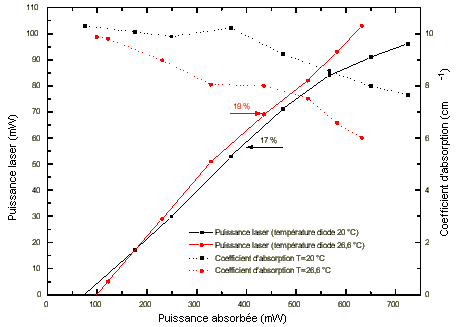
Les coefficients d'absorption représentés sur la figure ci-dessus sont des coefficients d'absorption moyens, c'est à dire les rapports entre la puissance incidente et la puissance transmise rapportés à la longueur du matériau actif. Ils ne tiennent pas compte des coefficients de réflexion des différentes interfaces. Les coefficients d'absorption diminuent quand le courant de diode augmente. Ce phénomène est dû à l'augmentation de la longueur d'onde d'émission de la diode et à son élargissement spectral résultant de l'augmentation de la température de jonction de la diode. Le spectre d'émission se décale par rapport au spectre d'absorption du matériau entraînant ainsi une absorption moins importante. Pour s'affranchir de ce problème, il faudrait maintenir une température constante au niveau de la jonction et avoir un système thermique capable d'évacuer toute la quantité de chaleur produite par la diode quelque soit son courant de fonctionnement.
Le spectre du faisceau laser émis autour de 1,53 µm pour un point de
fonctionnement particulier est représenté figure 5-23.
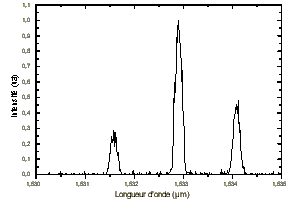
Il y a moins de modes longitudinaux que ce qui est prévu par la
théorie. En effet, le nombre de modes longitudinaux est relié à la longueur de cavité
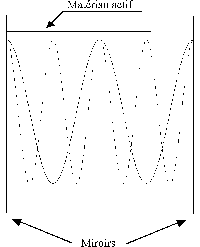
et à la largeur de la courbe de fluorescence (voir paragraphe 5) par :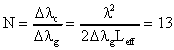 
avec 
: largeur à 90 % (voir paragraphe 5) du
spectre de fluorescence, Leff =5 mm : longueur optique de la cavité et 
: longueur d'onde. Il est possible que le nombre de modes présents
dans la cavité soit réduit par le phénomène de " brûlage de
trous " (" hole burning ") spatial.
Quand une onde stationnaire s'établit elle est composée de noeuds
(champ nul) et de ventres (champ maximal) (voir figure 5-24). A l'endroit du matériau
amplificateur où il y a un noeud l'amplification n'est pas affectée puisqu'il n'existe
pas à cet endroit de champ à amplifier. Par contre aux endroits présentant un ventre,
le champ à amplifier est maximal et donc sature le gain à cet endroit. On se retrouve
donc avec une modulation longitudinale du gain. Si une autre onde stationnaire ayant des
ventres proches de l'onde précédente veut prendre naissance, elle
" verra " à ces endroits un coefficient de gain
" appauvri " qui compensera moins ou pas du tout les pertes de la
cavité. Ce processus se rencontre dans les cavités à onde stationnaire (ici cavité
linéaire) de petite dimension (peu de modes longitudinaux). Il est d'autant plus
important que la transition d'émission du matériau est homogène. Dans notre cas la
transition est totalement inhomogène, ce qui devrait rendre ce mécanisme négligeable.
On peut voir sur la figure 5-25 que le profil spatial du faisceau au
point de focalisation est très proche d'une gaussienne parfaite.
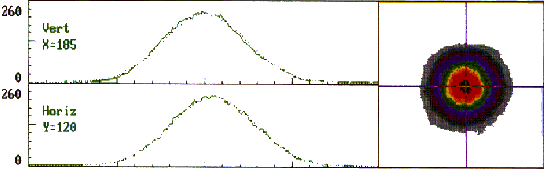
figure 5-25 : Profil spatial
du faisceau laser au point de focalisation
Le schéma expérimental est le même qu'au paragraphe 5.2.1.2.
L'évolution du rayon du faisceau à 
en fonction
de la position relative des points de mesure est représentée figure 5-26.
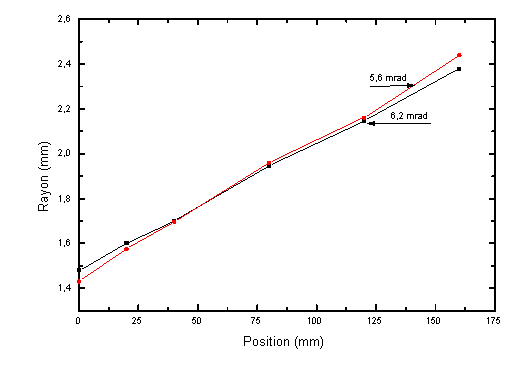
A partir de cette mesure, il est possible de la même manière qu'au paragraphe 5.2.1.2 de calculer la divergence du faisceau. On obtient une divergence d'environ 6 mrad quelque soit la direction.
Le schéma expérimental est le même qu'au paragraphe 5.2.1.3.
L'évolution du diamètre du faisceau à 
après
une lentille de focalisation en fonction de la position relative des points de mesure est
représentée figure 5-27.
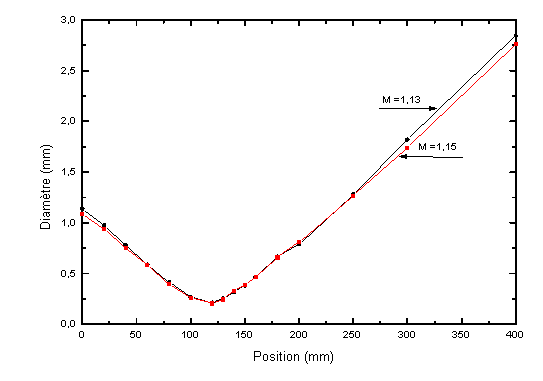
A l'aide de l'équation 5-1 et de la figure 5-27, on calcule un paramètre M moyen d'environ 1,15. Le faisceau est donc à peu près limité de diffraction.
A partir de la divergence et du coefficient de qualité du faisceau il
est possible de calculer le rayon du faisceau au point de focalisation : 
avec :
: divergence du faisceau,
: longueur d'onde,
w0 : dimension du mode au point de focalisation.
On a donc w080 µm.
Dans le paragraphe suivant nous allons nous intéresser aux contraintes
thermiques introduites par le faisceau de pompe au niveau du matériau laser.
La cavité utilisée dans toutes les expériences est une cavité à
miroirs plans parallèles. Cette cavité est naturellement instable, néanmoins cette
cavité peut être stabilisée soit par le guidage par le gain soit par une lentille
thermique. Dans notre cas, la lentille thermique introduite par l'élévation de
température due au pompage optique du matériau laser est une lentille divergente (
[22]).
Cette lentille thermique a donc pour effet de rendre instable la cavité laser. A forte
densité de puissance de pompe, ces effets peuvent dégrader notablement l'efficacité du
laser. En fait, un effet de balance existe entre le guidage par le gain et la lentille
thermique. A faible puissance de pompe, le guidage par le gain est plus important que la
lentille thermique on obtient donc une cavité stable. Par contre à forte puissance de
pompe la lentille thermique devient plus importante que le guidage par le gain et la
cavité tend à devenir instable.
Au début de ce travail de thèse, nous avons utilisé un autre verre codopé erbium et ytterbium (QE7S) fabriqué par Kigre Inc. dont les caractéristiques thermiques étaient moins intéressantes que celles du QX/ER [23].
Les différents coefficients thermiques de ces deux matériaux sont
présentés dans le tableau 5-2.
|
Coefficient d'expansion thermique (10-7 °C-1) |
conductivité thermique (W/m°K) |
|
QX/ER |
-10 |
82 |
0,85 |
QE7S |
-63 |
114 |
0,82 |
tableau 5-2 : Récapitulatif
des coefficients thermiques des deux matériaux.
Pour mettre en évidence ces problèmes thermiques nous avons utilisé
un laser He/Ne émettant à 632,8 nm de manière à visualiser sur une caméra les franges
d'interférences dues à un défaut de parallélisme des faces du matériau. Le matériau
a ensuite été pompé optiquement par une diode laser (voir paragraphe 5.3.1).
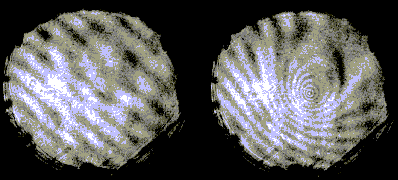
Le matériau QX/ER a été pompé avec une puissance de pompe de 650 mW
Le diamètre du faisceau de pompe au point de focalisation est 200 µm. Nous avons vu
défiler douze anneaux d'interférence " sortants " (voir figure
5-28).
Le matériau QE7S a été pompé avec une puissance de pompe de 340 mW
La dimension du point de focalisation du faisceau de pompe dans le matériau n'est pas
connu. Nous avons vu défilé neuf anneaux d'interférence
" sortants " (voir figure 5-29).
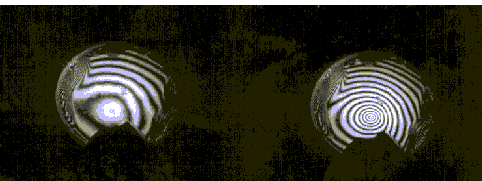
Le matériau QE7S a aussi été essayé avec les mêmes caractéristiques du faisceau de pompe que pour le matériau QX/ER mais le matériau s'est brisé au point de pompage sous l'effet de la puissance de pompe.
Le phénomène que nous visualisons à l'aide de ces franges d'interférence correspond à une modification de la longueur optique du matériau :
où n est l'indice et l la longueur du
matériau. Nous avons donc : 
.
et 
étant de signe
opposé (voir tableau 5-2) il est difficile de mettre en évidence l'effet de l'une ou de
l'autre des deux composantes de la variation de la longueur optique en fonction de la
température puisque ces deux effets se compensent.
Les deux matériaux ont été essayé en cavité laser dans la même configuration de pompe. Seule leur épaisseur diffère : le matériau QX/ER a une épaisseur de 2 mm alors que le matériau QE7S a lui une épaisseur de 1,2 mm. Ces résultats sont présentés figure 5-30.
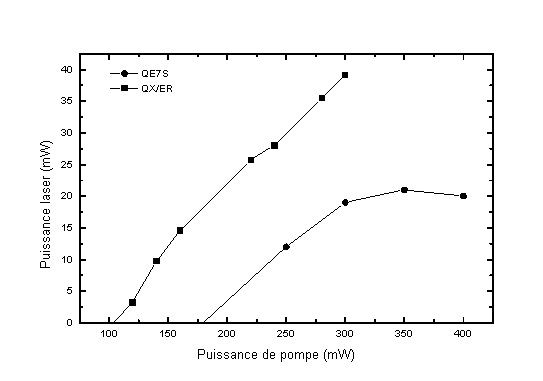
Pour le QE7S, nous voyons une limitation thermique de l'effet laser à partir d'une puissance de pompe de 300 mW alors que pour le QX/ER nous n'avons pas réussi à mettre en évidence des limitations thermiques.
Il est certain que ces effets thermiques vont dégrader l'effet laser quand nous essaierons d'utiliser des sources de pompage optique de puissance plus importante.
Nous allons maintenant présenter ce même laser déclenché par
commutation des pertes.
Les systèmes étudiés dans cette partie sont des systèmes de déclenchement par commutation des pertes. Le matériau actif est pompé en mode continu. Ce système se décompose en deux étapes (voir figure 5-31) :
Pour obtenir une impulsion courte et de puissance crête élevée, il faut que la commutation des pertes se fasse dans un temps très bref.
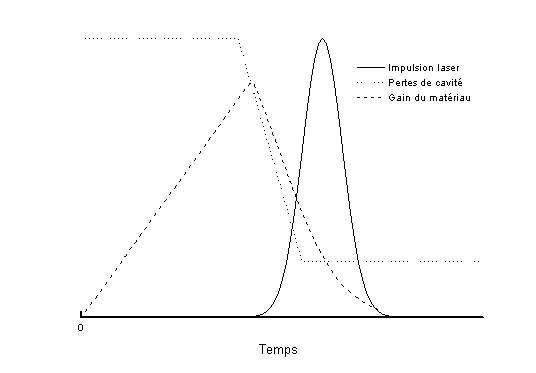
Il existe de nombreux moyens de déclencher un laser par commutation des pertes, mais ils peuvent se répertorier en deux catégories :
Les systèmes actifs sont caractérisés par la modification d'une propriété physique du système inséré dans la cavité grâce à une commande extérieure (effet acousto-optique, effet électro-optique ...). Cette modification entraîne une variation des pertes due à l'insertion du système dans la cavité.
Les systèmes passifs exploitent principalement les mécanismes d'absorption saturable. Dans ce cas, c'est l'effet laser lui-même qui modifie les propriétés du système inséré dans la cavité. (voir plus loin)
Pour déclencher notre laser, nous avons choisi deux composants actifs mécaniques et rudimentaires :
un diapason inséré dans la cavité qui alternativement coupe ou laisse
passer le faisceau laser.
Le dispositif expérimental est le même que celui présenté sur la figure 5-13. Un disque tournant présentant trois ouvertures de 0,5 mm (voir figure 5-34) est inséré dans la cavité entre le matériau actif et le miroir de sortie [24].
Dans ce régime, deux impulsions sont obtenues (voir figure 5-32) car le temps pendant lequel la cavité reste ouverte est assez long pour qu'une deuxième impulsion prenne naissance.
La largeur à mi-hauteur de la première impulsion est 
=35 ns.
Pour une puissance de pompe de 700 mW, l'énergie totale émise est mesurée à l'aide d'un joulemètre et d'un amplificateur. On mesure E=6 µJ. L'énergie contenue dans la première impulsion est E'=3,5 µJ.
La puissance crête est donc : 
La cadence de répétition est d'environ 400 Hz.
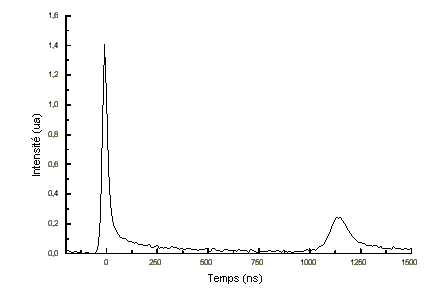
figure 5-32 : Évolution de
l'intensité laser en fonction du temps.
Le dispositif expérimental est le même que celui présenté sur la figure 5-13. Un diapason de 1 mm d'ouverture maximale et de fréquence de résonance 800 Hz est inséré dans la cavité entre le matériau actif et le miroir de sortie.
Dans ce régime, cinq ou six impulsions sont obtenues (voir figure 5-33) car le temps pendant lequel la cavité reste ouverte est plus long que dans le cas du disque tournant.
La largeur à mi-hauteur de la première impulsion est 
=60 ns.
Pour une puissance de pompe de 700 mW, l'énergie totale émise est mesurée à l'aide d'un joulemètre et d'un amplificateur. On mesure E=6 µJ. L'énergie contenue dans la première impulsion est E'=3 µJ.
La puissance crête est donc : 
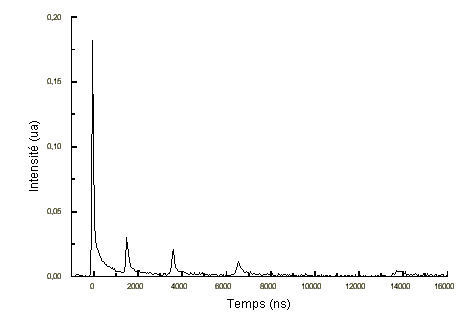
figure 5-33 : Évolution de
l'intensité laser en fonction du temps.
Le but de ce paragraphe est d'estimer les temps de commutation et les
temps pendant lesquels la cavité reste ouverte pour les deux systèmes présentés
précédemment.
Les temps de commutation de ces deux systèmes sont relativement lents.
L'énergie restituée n'est donc pas maximale.
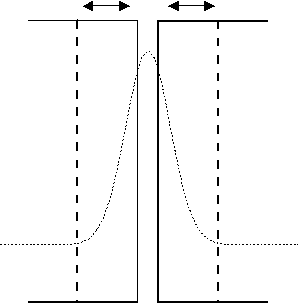
figure 5-34 : Schéma de
principe du fonctionnement du diapason et du disque tournant.
Nous allons exprimer l'évolution temporelle des pertes introduites par
ces deux systèmes. Ces systèmes coupent alternativement un faisceau de répartition
spatiale gaussienne.
Les pertes introduites dans la cavité par ces systèmes sont fonction
de l'intégrale de recouvrement entre la position du disque ou du diapason et le faisceau
gaussien intra-cavité rapportée à l'intégrale du faisceau gaussien. Ces équations
garantissent des pertes comprises entre 0 et 100 %.
avec w : rayon du faisceau laser au niveau du
disque, e : la largeur de la fente et 
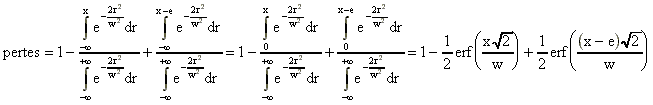
où v est la vitesse
linéaire du disque au point où se trouve le faisceau. 
avec r :
distance entre le centre du disque et le faisceau laser et f : la fréquence de rotation
du disque.
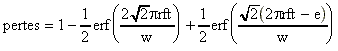
f = 133 Hz,
r = 6 cm,
e = 500 µm.
où x est la position instantanée d'un des
" doigts " du diapason.
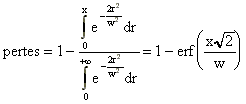
où c est le débattement total des
" doigts " et f, la fréquence de résonance du diapason.
c = 1 mm,
f = 800 Hz.
Dans les deux cas, w = 100µm.
Les variations temporelles des pertes pour les deux systèmes sont représentées sur la figure 5-35.
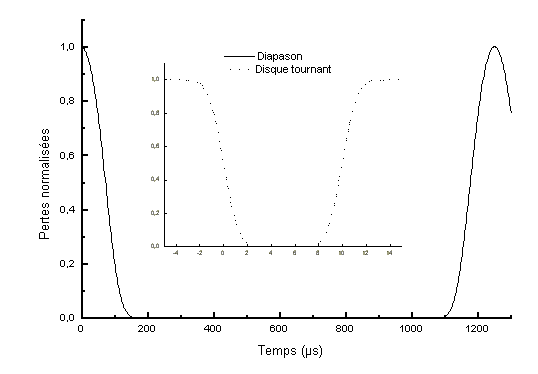
Les temps de commutation et les temps d'ouverture sont très différents
d'un système à l'autre.
Temps de commutation (10%-90%) |
Temps d'ouverture (inférieur à 1%) |
|
Diapason |
85 µs |
960 µs |
Disque tournant |
2,6 µs |
5,4 µs |
On peut voir notamment que le temps de descente des pertes introduites
par le disque tournant est environ 40 fois plus rapide que pour le diapason. On a donc une
meilleure restitution de l'énergie emmagasinée dans le cas du disque tournant que dans
le cas du diapason. De plus, le temps pendant lequel l'effet laser existe est presque 200
fois plus important pour le diapason que pour le disque tournant. On a donc beaucoup plus
d'oscillations de relaxation possibles dans le cas du diapason ce qui détériore encore
le fonctionnement en commutation des pertes.
Dans ces expériences où la source de pompage était une diode laser
fibrée, nous avons été limité par la puissance maximale délivrée par la diode ( 0,9
W). Il nous apparu intéressant d'augmenter cette puissance disponible soit pour augmenter
le rendement optique/optique du laser soit pour mettre en évidence des problèmes
thermiques du matériau laser utilisé. C'est dans cette optique que nous avons utilisé
une barrette de diodes laser associée à un " entonnoir " optique.
Les composants multi-laser sont en fait la juxtaposition sur un même substrat d'un certain nombre de lasers élémentaires dont les alimentations électriques sont connectées les unes avec les autres (voir figure 5-36). Le composant utilisé est une " barrette " d'environ 70 diodes élémentaires. Les miroirs définissant la cavité optique sont obtenus par dépôts multicouches de diélectrique :
Le régime quasi-continu est un fonctionnement impulsionnel dont la largeur d'impulsion est de l'ordre de grandeur de la durée de vie de l'ion actif du matériau laser à pomper (dans notre cas environ 10 ms) et dont le rapport cyclique est imposé par les contraintes d'évacuation thermique (dans notre cas 2%).
Dans la configuration quasi-continue le courant de seuil est plus
élevé (pertes plus importantes) et le rendement différentiel externe plus important
(coefficient de transmission de la cavité plus important) que dans la configuration
continue. En augmentant le courant de fonctionnement, on a donc une puissance optique plus
importante que dans la configuration continue sans pour autant être limité par les
effets thermiques.
figure 5-36 : Barrette de
diodes laser
La puissance émise en fonction du courant de fonctionnement pour la
barrette continue et la barrette quasi-continue sont représentées figure 5-37.
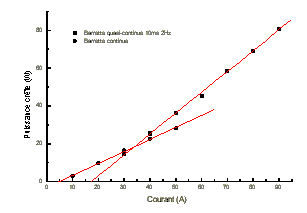
Les valeurs de courant de seuil et de rendement différentiel externe pour la barrette continue et la barrette quasi-continue sont présentées dans le tableau 5-4.
Barrette continue |
Barrette quasi-continue |
|
Courant de seuil (A) |
4,8 |
17 |
Rendement différentiel externe (W/A) |
0,63 |
1,1 |
Le faisceau émis par la barrette présente une divergence à mi-hauteur
de 37,5° dans le plan perpendiculaire à la jonction et de 7° dans le plan parallèle à
la jonction (voir figure 5-38).
Les barrettes de diodes laser sont des sources très étendues dans une direction ( 1 cm) et de très faible dimension dans l'autre ( 1 µm). Il est donc difficile avec ces sources d'obtenir un bon recouvrement des modes spatiaux du faisceau de pompe et du mode TEM00 d'une cavité laser. Le faisceau issu des barrettes nécessite donc une remise en forme pour pomper longitudinalement un laser solide. Il existe plusieurs méthodes pour symétriser le faisceau d'une barrette de diodes :
C'est cette dernière méthode que nous avons étudiée au sein du laboratoire. Ce système fut d'abord développé pour des barrettes de diodes émettant à 808 nm pour pomper des matrices dopées Néodyme [4][28].
Le système de l'entonnoir optique est fondé sur la réflexion totale
du faisceau sur une interface verre/air. L'effet " entonnoir " n'agit
que dans une seule direction où l'on passe de 11 mm à 1,5 mm. L'autre direction
présente une épaisseur constante de 1,5 mm. La surface d'entrée est une lentille
cylindrique de rayon de courbure de 9,8 mm. La barrette présentant une divergence de 7°
dans le plan parallèle à la jonction, on a donc une divergence de 
en sortie d'" entonnoir " alors que dans le plan
perpendiculaire à la jonction la divergence reste de 37°.
Un tracé de rayons a été effectué (voir figure 5-39) pour confirmer
ce calcul et pour prévoir le coefficient de couplage de la barrette dans
l'" entonnoir ".
On trouve un couplage théorique de 87 % dans le cas où les faces
d'entrée et de sortie de l'" entonnoir " ne sont pas traitées
antireflet à 980 nm et de 92 % dans le cas où celles-ci présentent un traitement
antireflet parfait. Le couplage mesuré est de l'ordre de 90 % aussi bien avec la barrette
continue qu'avec la barrette quasi-continue.
L'association de la barrette et de l'" entonnoir " optique est représenté figure 5-40.
Nous ne présentons pas dans ce mémoire de résultats concernant le
pompage optique par la barrette continue car lors d'un essai préliminaire le matériau
laser s'est mis à fondre pour une puissance en sortie d'" entonnoir "
de l'ordre de 5 W.
figure 5-40 : Barrette de diodes laser et entonnoir optique
Le schéma de l'expérience est présenté figure 5-41.
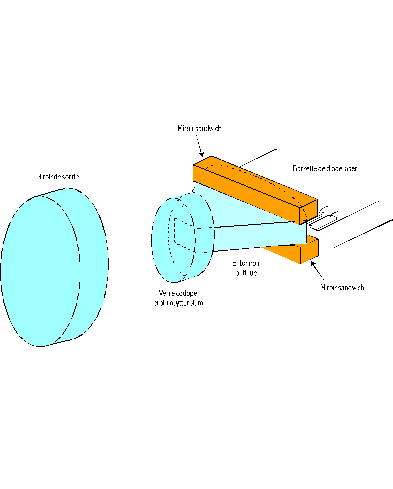
figure 5-41 : Schéma de la
cavité
Les performances du laser ainsi obtenues sont présentées figure 5-42.
Le miroir de sortie présente une réflectivité de 99% à la longueur d'onde laser. Le
matériau actif a une longueur de 2mm. Une face présente une réflectivité maximale à
1,54 µm ainsi qu'une bonne transmission (>98%) à la longueur d'onde de pompe quelque
soit l'angle d'incidence (0<
<50°). L'autre face présente
une bonne transmission (>99,9%) à la longueur d'onde laser. La longueur totale de la
cavité est d'environ 2 cm.
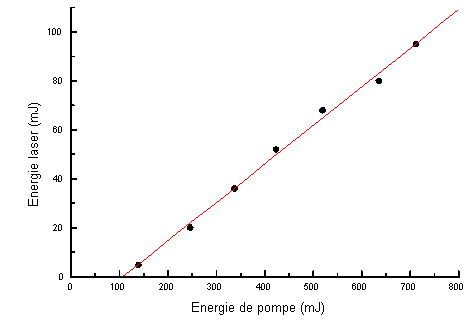
figure 5-42 : Énergie laser
en fonction de l'énergie de pompe
Le laser ainsi réalisé a une énergie de pompe au seuil de 105 mJ et
un rendement différentiel externe de 15,8 %. Le mode obtenu n'est pas TEM00
car la répartition spatiale de l'énergie est proche d'un carré.
Nous avons vu au paragraphe 4.3 qu'il était possible d'estimer le
coefficient de transfert d'énergie de l'ion ytterbium vers l'ion erbium (k) grâce à
l'équation 4-5 de la page 1 dont le temps de décroissance est : 
. Les seuls paramètres inconnus dans ce terme sont k et n2seuil, il
paraît donc possible d'évaluer n2seuil pour calculer k.
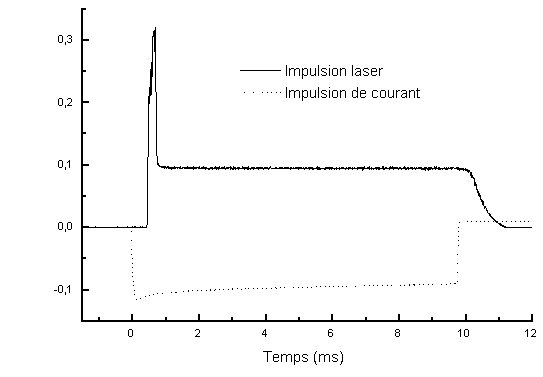
Le temps de décroissance de l'impulsion laser est mesuré sur la figure
5-43. On trouve 
400 µs. Nous avons estimé que n2seuil
était compris entre 0,6 et 0,8. Cette estimation sera vérifiée lors des calculs avec
notre modèle mathématique.
On a donc :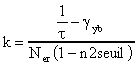 
. On trouve 3,1.10-22
m3s-1<k< 6,2.10-22 m3s-1.
L'intensité de pompe engendrée par l'association de la barrette de diodes laser et de l'" entonnoir " optique est très importante. Les effets thermiques sur le matériau actif doivent être importants. C'est pourquoi nous avons décidé de nous intéressé à la biréfringence thermique. Les pertes introduites pourraient limiter considérablement l'emploi de systèmes de commutation des pertes habituellement utilisés.
Le faisceau d'un laser HeNe polarisé et collimaté éclaire la zone du
matériau actif pompée par la barrette associée à l'" entonnoir "
optique (voir figure 5-44). Le diamètre du faisceau du laser HeNe est inférieur à la
dimension de la zone excitée du matériau actif. La réflexion du laser sonde sur les
deux faces du matériau est collecté par un détecteur par l'intermédiaire d'un
polariseur. La surface du détecteur est plus importante que la surface du faisceau de
retour, et sa bande passante est suffisante pour visualiser les effets cherchés.
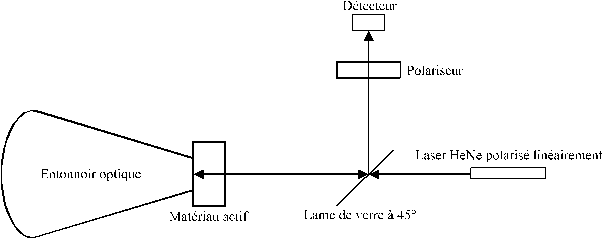
figure 5-44 : Schéma de
l'expérience
Les oscillogrammes du signal de retour et de l'impulsion de courant sont
présentés sur la figure 5-45.
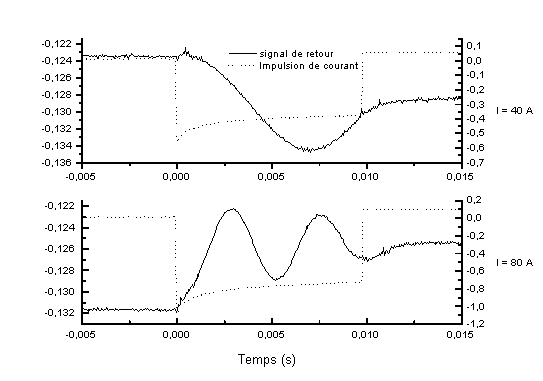
Le signal de retour à travers le polariseur varie en fonction du temps, on a donc une rotation de la polarisation durant l'impulsion de pompe. La période et l'amplitude de ces oscillations varient avec l'énergie déposée par la pompe. En faisant varier rapidement l'énergie déposée d'une valeur à une autre les oscillations mettent quelques secondes à se stabiliser. La rotation de la polarisation est donc due au faisceau de pompe.
Les pertes introduites par cette biréfringence thermique sont de l'ordre de grandeur du gain de notre laser. Il n'est donc pas possible d'introduire dans cette cavité un élément sélectionnant la polarisation.
Ces pertes limitent considérablement l'emploi des méthodes actives de
commutation des pertes habituellement utilisées dans les lasers solides (effet
acousto-optique et effet électro-optique) du fait de leur influence sur la polarisation
du laser. Il apparaît donc très intéressant d'exploiter les mécanismes d'absorption
saturable pour déclencher ce type de laser.
Les mesures des dimensions des modes laser et des modes de pompe, des
divergences et des coefficients de qualité des faisceaux, l'estimation du coefficient de
transfert d'énergie ainsi que les différentes courbes de puissance laser en fonction de
la puissance de pompe effectués dans cette partie vont nous permettre dans la partie
suivante de valider notre modèle mathématique aussi bien en fonctionnement continu que
déclenché.
Chapitre suivant
selon deux directions perpendiculaires en
pompage par diode laser. 
après une lentille de focalisation
selon deux directions perpendiculaires en pompage par diode laser.
(10-7 °C-1)