2. Fonction de distribution du module de vitesse
3. Calcul d’une valeur moyenne
4. Retour sur la loi de distribution des vitesses
5. Pression d’un gaz parfait
6. Le facteur de Boltzmann
Intégrales
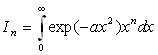
Annexe : la loi de distribution des vitesses de Maxwell
Plan
1. Fonction de distribution du vecteur vitesse
2. Fonction de distribution du module de vitesse
3. Calcul d’une valeur moyenne
4. Retour sur la loi de distribution des vitesses
5. Pression d’un gaz parfait
6. Le facteur de Boltzmann
Intégrales 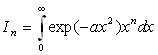
1. Fonction de distribution du vecteur vitesse
Pour un gaz en état d’équilibre, posons la question
suivante :
Quelle probabilité existe qu’une molécule ait ses composantes
de vitesse comprise entre vx et vx
+ dvx , vy
et vy + dvy
, vz et vz
+ dvz (repère cartésien
habituel) ?
Cette probabilité d3P
dépend de ![]() (c’est
à dire vx , vy
, vz ) et de dvx
, dvy , dvz
. Elle ne dépend pas de la position de la molécule puisque le
gaz est en équilibre.
(c’est
à dire vx , vy
, vz ) et de dvx
, dvy , dvz
. Elle ne dépend pas de la position de la molécule puisque le
gaz est en équilibre.
Nous postulons que d3P est proportionnelle
à chacun des intervalles dvx ,
dvy , dvz
.
![]()
Il n’y a pas de direction privilégiée. Nous pouvons
faire une rotation circulaire des axes cartésiens, la probabilité
sera inchangée (isotropie de l’espace).
La fonction ![]() ne
dépend pas du vecteur
ne
dépend pas du vecteur ![]() ,
au mieux elle dépend de l’intensité de vitesse v.
,
au mieux elle dépend de l’intensité de vitesse v.
![]()
Soit dPx la probabilité
pour une molécule d’avoir sa composante suivant l’axe Ox comprise entre
vx et vx
+ dvx .
![]() de même
de même
![]() et
et ![]()
L’isotropie de l’espace impose ![]()
La loi des probabilités composées implique :
![]()
Déterminer les fonctions f et j
relève de la méthodologie mathématique suivante :
![]() avec
avec ![]()
En réorganisant, on obtient : ![]()
Le membre de gauche dépend de v c’est à
dire de vx , vy
, vz , celui de droite uniquement de
vx . Le résultat ne peut être
qu’une constante que nous notons a .
Il suit que : ![]()
Soit, ![]() et des expressions identiques pour
et des expressions identiques pour ![]() .
.
Alors ![]()
Remarquons que a est nécessairement
négatif sinon la probabilité pour une molécule d’avoir
une composante de vitesse infinie serait infinie ce qui voudrait dire que toutes
les molécules seraient à vitesse infinie et que l’énergie
serait infinie !!!
Nous posons a / 2 =-B avec B > 0.
![]()
La condition de normalisation
La probabilité pour une molécule d’avoir une
composante de vitesse comprise entre -![]() et +
et +![]() ou une intensité de
vitesse comprise entre 0 et +
ou une intensité de
vitesse comprise entre 0 et +![]() est
égale à 1 (100% de chances).
est
égale à 1 (100% de chances).
Ainsi, 
Remarque
Nous avons parlé en terme de probabilité. Un
langage équivalent consiste à chercher, dans une enceinte contenant
N molécules, le nombre dN de molécules ayant certaines
caractéristiques, à savoir par exemple, le nombre de molécules
![]() ayant une composante
de vitesse comprise entre vx et vx
+ dvx .
ayant une composante
de vitesse comprise entre vx et vx
+ dvx .
Ce nombre est égal à : ![]()
2. Fonction de distribution du module de vitesse
Quelle est la probabilité dP(v) pour une molécule
d’avoir une intensité de vitesse comprise entre v et v+dv
? ou combien y a t’il de molécules dN(v) dans une enceinte contenant
N molécules ayant une intensité de vitesse comprise entre
v et v+dv ?
Pour répondre à cette question, nous nous plaçons dans
l’espace des vitesses c’est à dire un repère cartésien
de coordonnées Ovx , Ovy
, Ovz .
|
|
Les composantes vx
, vy , vz
ne sont pas indépendantes puisque liées par la relation
L’extrémité des vecteurs vitesse |
Dans l’espace des vitesses, nous délimitons une portion
d’espace comprise entre la sphère de rayon v + dv et la sphère
de rayon v, de volume égal à ![]() .
.
La probabilité d3P est proportionnelle
à ![]() c’est
à dire au volume élémentaire dans l’espace de vitesse.
Pour obtenir dP(v), nous devons intégrer d3P
à tous les vecteurs vitesse possibles c’est à dire ayant leur
extrémité entre les deux sphères.
c’est
à dire au volume élémentaire dans l’espace de vitesse.
Pour obtenir dP(v), nous devons intégrer d3P
à tous les vecteurs vitesse possibles c’est à dire ayant leur
extrémité entre les deux sphères.
Cette intégration est particulièrement simple puisque l’intensité
v de la vitesse dans cette espace est constante.
On obtient donc : 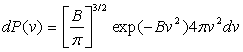
et aussi, dans une enceinte contenant N molécules, le nombre de molécules dN(v) ayant un module de vitesse compris entre v et v + dv : dN(v) = N dP(v).
3. Calcul d’une valeur moyenne
La valeur moyenne <G> d’une grandeur G est le produit de G multiplié (pondérée) par la probabilité d’obtenir G intégré à toutes les valeurs possibles de cette grandeur.
Ainsi,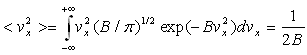 et
et 
Remarque : ![]()
4. Retour sur la loi de distribution des vitesses
La mesure, pour un gaz parfait monoatomique, de la capacité
calorifique à volume constant, conduit à : ![]()
Si nous formulons l’hypothèse que la partie de l’énergie
liée à la température est due à l’agitation cinétique
des molécules, nous pouvons écrire :
![]() ð
ð
![]()
Nous disposons de deux expressions de la vitesse quadratique
moyenne.
![]()
Les expressions de distribution des vitesses deviennent : 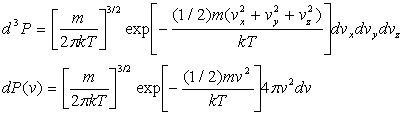
On a vu (3.1.2.) l’interprétation microscopique de la pression liée aux chocs des molécules sur une paroi.
Nous considérons le choc des molécules sur un élément de paroi dS que nous prenons arbitrairement perpendiculaire à l’axe Ox. Le gaz étant en état d’équilibre, toutes les directions sont équivalentes.
|
|
Soient |
Combien de molécules de vecteur vitesse ![]() frappent la paroi dS pendant un temps dt ?
frappent la paroi dS pendant un temps dt ?
Elles sont contenues dans un cylindre de base dS, de génératrice
parallèle à ![]() de
longueur
de
longueur ![]() . Le
volume de ce cylindre est égal à
. Le
volume de ce cylindre est égal à ![]() .
.
Le nombre de molécules sera ![]() si N est le nombre de molécules contenues dans l’enceinte de volume
V.
si N est le nombre de molécules contenues dans l’enceinte de volume
V.
La quantité de mouvement transmise à la paroi par ces molécules
est ![]() que nous
devons intégrer à toutes les molécules venant frapper la
paroi.
que nous
devons intégrer à toutes les molécules venant frapper la
paroi.
Soit 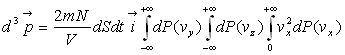
Les deux premières intégrales sont égales
à 1, la troisième à ![]()
En appliquant le principe fondamental de la dynamique, on obtient
la pression à partir de
![]()
Retrouver l’équation d’état des gaz parfaits prouve la validité et la cohérence des hypothèses formulées.
Nous avons introduit la notion de degré de liberté
(possibilité d’énergie indépendante) et avons trouvé
que, dans le cas du mouvement de translation suivant un axe, par exemple Ox,
le nombre de molécules ![]() ayant une composante de vitesse vx est
proportionnel à
ayant une composante de vitesse vx est
proportionnel à ![]() .
.
![]() représente l’énergie E suivant ce degré de liberté.
représente l’énergie E suivant ce degré de liberté.
Nous généralisons ce résultat en admettant
que le terme ![]() ,
appelé facteur de Boltzmann, caractérise la probabilité
d’occupation du niveau d’énergie E dans une situation d’équilibre
thermique à la température T.
,
appelé facteur de Boltzmann, caractérise la probabilité
d’occupation du niveau d’énergie E dans une situation d’équilibre
thermique à la température T.
Remarques :
En effet, pour la fonction de distribution du module de vitesse,
nous avons trouvé  .
.
Ecrite en terme d’énergie, l’expression ci-dessus
devient ![]() et
la probabilité est proportionnelle à
et
la probabilité est proportionnelle à ![]() et non au facteur de Boltzmann.
et non au facteur de Boltzmann.
En fait ![]() :
les trois degrés de liberté affectés à chaque
translation ne sont pas indépendants.
:
les trois degrés de liberté affectés à chaque
translation ne sont pas indépendants.
Remarque : Certains trouveront désuet, dépassé, ce cours sur la loi de distribution des vitesses de Maxwell (appelé aussi Théorie cinétique des gaz parfaits), pire réducteur dans la formation d’un étudiant puisqu’il ne met pas en évidence qu’au sens quantique, la Physique est probabiliste par essence.
Le raisonnement probabiliste de Maxwell est induit par l’incapacité à connaître pour un très grand nombre de particules leur position et leur vitesse à chaque instant. Ce raisonnement ne remet pas en cause le déterminisme en Physique à savoir, à chaque instant, chaque particule possède une position et une quantité de mouvement fixées. Le raisonnement de Maxwell est probabiliste par ignorance.
La mécanique quantique et l’inégalité de Heisenberg infirment la possibilité de connaissance exacte de la position et de la quantité de mouvement d’une particule –on doit introduire la notion d’occupation d’une case de dimension finie dans l’espace de phase, et de saut pour passer d’une case à une autre. Le raisonnement probabiliste devient incontournable et la Physique est probabiliste par essence.
Cette nouvelle façon d’appréhender la Physique s’est développée à partir du début du 20ème siècle, nous la croyons trop récente pour être enseignée trop vite à des étudiants qui ne maîtrisent pas suffisamment de connaissances en Physique …d’autant que notre sens commun, au niveau macroscopique, est essentiellement déterministe.
Nous intégrons par parties en posant ![]()
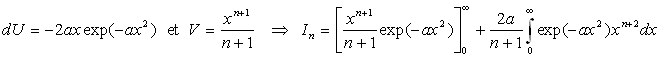
Nous obtenons une relation de récurrence ![]()
A ce stade, nous devons calculer I1 et I0 .
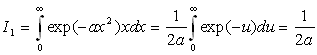
![]()
Le calcul de I0 est plus complexe.
 et
et 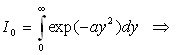
![]()
|
|
|