Chapitre 9 : Etude thermodynamique des changements
de phases des corps purs
Plan
1. Définition de la chaleur latente
de changement de phase (d’état) d’un corps pur
2. Etude énergétique
2.1. Définition du titre. Règle du levier.
2.2. Relations de Clapeyron
3. Etablissement des bases de données sur les fonctions
d'état
4. Mesure des chaleurs latentes
4.1. Dispositifs expérimentaux
4.2. Résultats
Le lecteur se reportera avec intérêt au chapitre
"Structure de la matière" paragraphe "changements de phases".
1. Définition de la chaleur latente
de changement de phase (d’état) d’un corps pur
L'étude des changements de phases (chapitre Structure
de la matière) nous a montré que la température est fixée
pour un corps pur sous deux phases quelques soient la proportion (massique ou
volumique) de deux phases.
Par expérience quotidienne, nous savons que nous échangeons de
la chaleur lorsque nous réalisons un changement de phases mais, à
ce stade du cours, les seules expressions théoriques d'échanges
de chaleur sont limitées aux systèmes sous une seule phase.
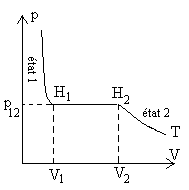
Il s'agit de traduire l'échange de chaleur lorsque nous passons de l'état
1 à l'état 2 à pression constante  .
.
L'écriture de la variation d'enthalpie et l'écriture
du premier principe pour le changement de phases permet d'écrire :

|
|
Définition
On appelle chaleur latente (massique ou molaire) de changement
d’état d’un corps pur à la température T la
variation d’enthalpie (de l’unité de masse ou d’une mole) de ce
corps passant d’un état (solide, liquide ou gazeux) à un
autre état.
Outre la mesure des capacités calorifiques, la Calorimétrie
a pour objet la mesure des Chaleurs latentes. La description des dispositifs
expérimentaux et les résultats sont exposés à
la fin du chapitre
|
Les chaleurs latentes sont symboliquement notées 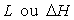 .
Ainsi
.
Ainsi 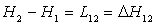 , variation
d’enthalpie de l'état 1 à l'état 2 est la chaleur latente
pour passer de l'état 1 à l'état 2 suivant l’isobare de
pression
, variation
d’enthalpie de l'état 1 à l'état 2 est la chaleur latente
pour passer de l'état 1 à l'état 2 suivant l’isobare de
pression 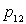 .
.
Les chaleurs latentes de fusion  (transition solide à liquide), de vaporisation
(transition solide à liquide), de vaporisation
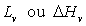 (transition liquide
à vapeur) et de sublimation
(transition liquide
à vapeur) et de sublimation  (transition solide à gaz) sont positives
c’est à dire qu’il faut fournir de la chaleur pour faire fondre un solide,
vaporiser un liquide ou sublimer un solide.
(transition solide à gaz) sont positives
c’est à dire qu’il faut fournir de la chaleur pour faire fondre un solide,
vaporiser un liquide ou sublimer un solide.
Les chaleurs latentes de solidification, de condensation à l’état
liquide et de condensation à l’état solide sont respectivement
opposées à celles de fusion, de vaporisation et de sublimation.
2. Etude énergétique
2.1. Définition du titre. Règle
du levier.
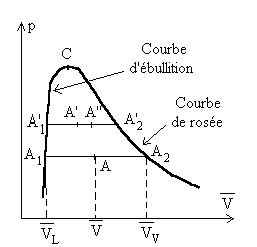
L'étude sera menée à partir de l'équilibre liquide-vapeur. Mis à part ce qui sera présenté autour du point critique C, les résultats sont généralisables aux équilibres solide-liquide et solide-gaz.
|
|
Nous raisonnons sur une unité de masse de corps pur et considérons les deux paliers de liquéfaction A1A2 et A’1A’2 à température T et T + dT.
On appelle x le titre de vapeur saturante défini
comme étant la proportion en masse de vapeur dans le mélange
liquide-vapeur.
Pour l’unité de masse de corps, x est la masse de vapeur
et 1 - x la masse de liquide.
Soit 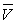 le volume du mélange liquide-vapeur dans l’état A.
le volume du mélange liquide-vapeur dans l’état A.
 ; ;  sont des fonctions de T suivant la courbe de rosée et la
courbe d’ébullition.
sont des fonctions de T suivant la courbe de rosée et la
courbe d’ébullition.
|
La pression de vapeur saturante étant une fonction de
T, les variables d’état indépendantes pour le mélange
liquide-vapeur sont x et T.
La quantité de chaleur Q échangée pour passer de
A1 à A suivant le palier de liquéfaction
est :
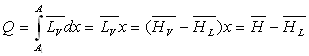
L’énergie interne en A sera :

L’entropie en A sera :

On remarquera l’analogie des formules donnant le titre en fonction des volumes, des enthalpies, des énergies internes et des entropies.
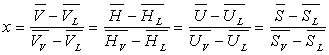
2.2. Relations de Clapeyron
Capacités calorifiques massiques de vapeur saturante et de liquide saturant
Soit dQ’ la quantité de chaleur échangée dans la transformation allant de A2 à A'2 suivant la courbe de rosée.
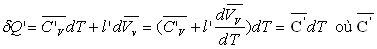 est la capacité calorifique massique de la vapeur saturante.
est la capacité calorifique massique de la vapeur saturante.
De même, suivant la courbe d’ébullition, on définit
la capacité calorifique massique du liquide saturant 
La capacité calorifique du liquide saturant est très
proche (sauf au voisinage du point critique) de la capacité calorifique
du liquide à volume constant.
La capacité calorifique de la vapeur saturante est inférieure
et très différente de celle de la capacité calorifique
à volume constant de la vapeur sèche. Elle est assez souvent négative,
ce qui veut dire que, pour diminuer la température d’une vapeur saturante,
il faut lui fournir de la chaleur.
Pour l’unité de masse de corps, nous considérons la transformation
de l’état A(x, T) à l’état A’’(x+dx, T+dT)
en utilisant l’état intermédiaire A’(x, T+dT).
La quantité de chaleur échangée pour passer
de l’état A à l’état A’’ est :
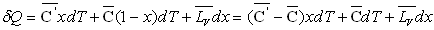
La variation d’entropie entre A et A" sera :
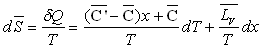
La variation d’enthalpie entre A et A’’ sera :
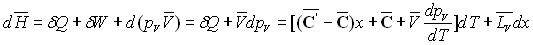
La relation de Cauchy appliquée aux deux différentielles
totales 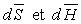 permet
d'écrire :
permet
d'écrire :
 ð
ð
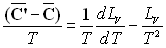
 ð
ð 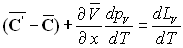
En tenant compte de la relation 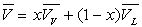 ,
on obtient sans difficulté particulière les très importantes
relations de Clapeyron.
,
on obtient sans difficulté particulière les très importantes
relations de Clapeyron.
|
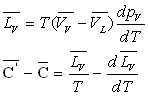
|
Pour les équilibres solide-liquide et solide-gaz, nous pouvons faire des raisonnements analogues et obtenir :
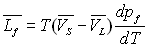 et
et 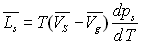
|
Il existe plusieurs démonstrations des relations de Clapeyron, celle (non présentée) faisant intervenir la fonction d’état enthalpie libre et la notion de potentiel chimique nous parait la plus intéressante.
" Justification " des formules de Dupré et Rankine
Loin du point critique, 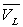 est très inférieur à
est très inférieur à 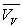 (pour l’eau
(pour l’eau 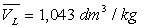 et
et 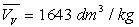 à
100 °C ; la température critique est 374,2 °C)
à
100 °C ; la température critique est 374,2 °C)
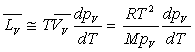 si
on admet que la vapeur sèche jusqu’à sa limite saturante obéit
à l’équation d’état des gaz parfaits.
si
on admet que la vapeur sèche jusqu’à sa limite saturante obéit
à l’équation d’état des gaz parfaits.
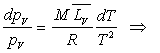 formule
de Dupré si
formule
de Dupré si  pour l’intervalle de température ou formule de Rankine si
pour l’intervalle de température ou formule de Rankine si 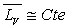 .
.
3. Etablissement des bases de données
sur les fonctions d'état
Les ingénieurs thermodynamiciens et les chimistes ont
établi (établissent), en regroupant, recoupant et analysant les
résultats expérimentaux, des bases de données leur permettant
d'accéder facilement, à différentes températures
et différentes pressions, aux valeurs rendant compte des propriétés
de la matière.
Ces bases de données (qui, pour un grand nombre de corps, sont du domaine
public) sont présentées sous forme de tables, de diagrammes ou
de logiciels.
Il faut distinguer :
- les données, sur les volumes spécifiques
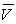 (ou les masses volumiques
(ou les masses volumiques 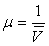 ), sur les températures de fusion, d'ébullition,
sur les températures critiques, sur les coefficients thermoélastiques,
… qui s'obtiennent directement à partir de dispositifs expérimentaux
conçus pour en faire la mesure,
), sur les températures de fusion, d'ébullition,
sur les températures critiques, sur les coefficients thermoélastiques,
… qui s'obtiennent directement à partir de dispositifs expérimentaux
conçus pour en faire la mesure,
- des données sur les fonctions d'état utiles en Thermodynamique c'est à dire :
- l'énergie interne
 ,
,
- l'enthalpie
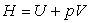 ,
,
- l'entropie
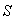 ,
,
- l'énergie libre
 ,
,
- l'enthalpie libre
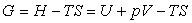
qui sont déterminées après calcul.
Nous remarquons que la connaissance de l'enthalpie et de l'entropie suffisent pour déterminer toutes les fonctions d'état et nous limitons notre propos sur l'établissement des bases de données sur les fonctions d'état aux corps purs.
Pour un corps pur, sous une phase, nous avons établi
les relations :
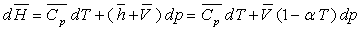 ð
ð 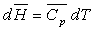 à pression constante
à pression constante
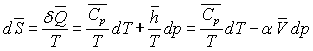 ð
ð  à pression constante
à pression constante
L'enthalpie est connue de manière relative (à
une constante additive près) alors que l'entropie est connue de manière
absolue compte tenu du 3ème principe de la Thermodynamique
(Un corps à température absolue nulle a une entropie nulle)
En ce qui concerne l'enthalpie, on définit un état de référence
où on pose que l'enthalpie est nulle. Cet état de référence
est celui de l'état des corps purs simples à la température
de 298 K et à la pression de 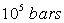 .
.
En fait, comme on ne calcule que des variations des fonctions d'état entre deux états différents, la notion d'état de référence pour calculer la valeur d'une fonction d'état n'a pas une grande acuité.
Ainsi le long d'une isobare, pour un corps ne changeant pas
de phase,
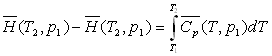 et
et 
Lors d'un changement d'une phase 1 à une phase 2, celui-ci
se produisant à température  et à pression
et à pression 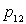 fixées, on obtient :
fixées, on obtient :
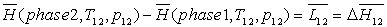

4. Mesure des chaleurs latentes
4.1. Dispositifs expérimentaux
Chaleur latente de fusion
On utilise un calorimètre adiabatique dans lequel est
maintenu à une température constante 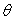 légèrement supérieure à la température de
fusion
légèrement supérieure à la température de
fusion 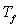 du corps
à étudier. On y introduit une masse m de ce corps à
une température
du corps
à étudier. On y introduit une masse m de ce corps à
une température  légèrement inférieure à
légèrement inférieure à 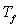 (le corps est donc en phase solide) ; on maintient la température
du calorimètre constante à l’aide d’une résistance immergée
dans le calorimètre et parcourue par un courant électrique réglable.
(le corps est donc en phase solide) ; on maintient la température
du calorimètre constante à l’aide d’une résistance immergée
dans le calorimètre et parcourue par un courant électrique réglable.
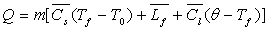 ,
,
si Q est la quantité de chaleur fournie par effet Joule,  les capacités calorifiques massiques du corps à l’état
solide et liquide et
les capacités calorifiques massiques du corps à l’état
solide et liquide et  la chaleur latente massique de fusion du corps.
la chaleur latente massique de fusion du corps.
Chaleur latente de vaporisation
- Appareillage simple (appareil de Berthelot ; appareil de Richards)
|

Appareil de Richards |
Un vase Dewar est traversé par un tube T ouvert
à ses deux extrémités. Ce tube se raccorde à
un serpentin S plongé dans un calorimètre adiabatique. Le
serpentin aboutit à un réservoir de condensation R et communique
avec l’atmosphère par le tube A . L’ébullition du liquide
placé dans le vase Dewar a lieu ainsi sous la pression atmosphérique.
Des gouttes liquides peuvent provenir d’une légère condensation
qui se produit dans la vapeur en montant dans le vase Dewar. Elles sont
vaporisées à nouveau lorsqu’elles traversent le fond dans
le tube T et la vapeur arrivant dans S est sèche.
L’égalité de température entre le calorimètre
et l’enceinte E est obtenue en faisant tomber de l’acide dans la solution
de soude contenue dans E.
|
|
|
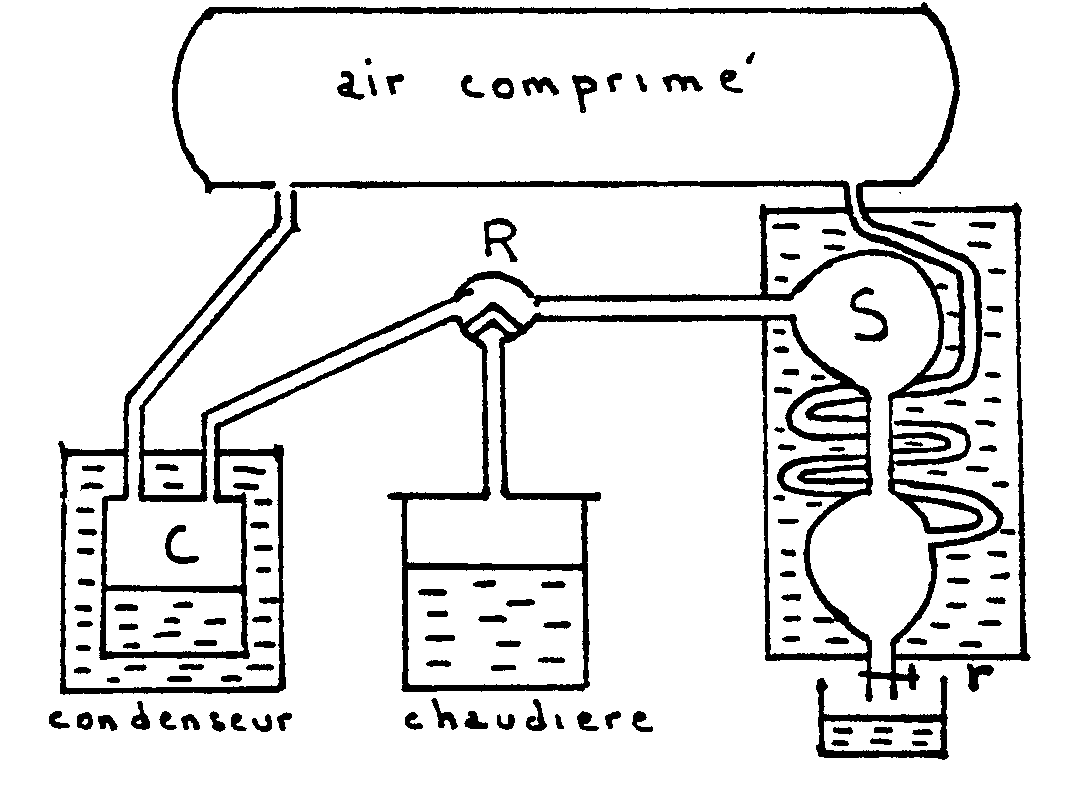
L’appareil est entièrement clos et la pression
intérieure est obtenue grâce à une atmosphère
artificielle (réservoir de 600 litres pouvant supporter des pressions
inférieures à 20 atmosphères). Un robinet R permet
de mettre la chaudière en communication soit avec un condenseur
C, soit avec un serpentin de condensation S.
Au début, la chaudière communique avec le condenseur et
on chauffe le liquide (eau) jusqu’à ébullition ; les
vapeurs viennent se condenser dans C.
|
Quand la distillation est devenue régulière,
on met la chaudière en communication avec le serpentin. La vapeur sèche
qui arrive s’y condense et quand l’expérience a duré assez longtemps,
on remet la chaudière en communication avec le condenseur, puis on recueille
avec le robinet r l’eau condensée en S.
Désignons par m la masse du liquide condensé,  sa capacité calorifique massique,
sa capacité calorifique massique, 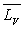 sa chaleur latente de vaporisation sous la pression considérée
à la température
sa chaleur latente de vaporisation sous la pression considérée
à la température  et
et  la valeur
en eau du calorimètre dont la température initiale est
la valeur
en eau du calorimètre dont la température initiale est  et la température finale
et la température finale 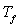 .
.
Le bilan énergétique s’écrit : 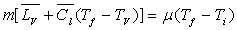
Cette méthode se prête très facilement à la mesure des chaleurs de vaporisation.
L’augmentation de volume 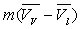 produite par la vaporisation est égale au volume de vapeur
produite par la vaporisation est égale au volume de vapeur  sorti de la chaudière ð
sorti de la chaudière ð 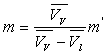 .
.
m diffère d’autant plus de m’ que l’écart 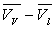 est plus faible c’est à dire que l’on s’approche de la température
critique.
est plus faible c’est à dire que l’on s’approche de la température
critique.
Le tableau ci-après donne les valeurs pour l’eau.
|
Températures |

|
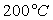
|
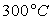
|

|
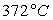
|

|
|
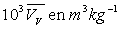
|
1,673 |
0,1272 |
0,02162 |
0,00500 |
0,00450 |
0,00323 |
|
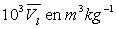
|
0,001043 |
0,001156 |
0,001404 |
0,00223 |
0,00238 |
0,00323 |
4.2. Résultats
Chaleur latente de fusion
Sous la pression atmosphérique, pour différents corps :
- 333 kj/kg pour l’eau à 0 °C
- 20,5 kj/kg pour le phosphore à 44 °C
- 22,5 kj/kg pour le plomb à 327 °C
Chaleur latente de vaporisation
|

|
Les chaleurs latentes de vaporisation diminuent avec
la température et atteignent une valeur nulle au point critique
puisque phases liquide et gazeuse sont identiques.
On utilise souvent des lois empiriques du type 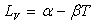 dans un intervalle de température.
dans un intervalle de température.
Ainsi pour l’eau entre 100 et 200 °C,

|
Nous donnons ci-après quelques chaleurs latentes massiques de vaporisation exprimées en kj/kg sous une pression d’un atmosphère.
Ammoniac 1425 ; Benzène 393 ; Dioxyde
de Carbone 594 ; Eau 2253 ; Dioxyde de Soufre 397 ; Ethanol 903
L’importances des valeurs des chaleurs latentes et, plus particulièrement, de celles de vaporisation justifie l’utilisation des changements de phase dans beaucoup de machines thermiques.
Les chaleurs latentes de fusion, de sublimation et de vaporisation sont positives, celles de solidification, de condensation à l’état solide et de condensation à l’état liquide sont respectivement égales et opposées.



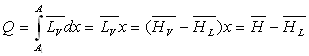

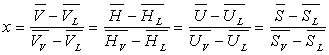
 ð
ð
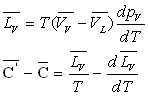
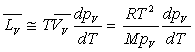 si
on admet que la vapeur sèche jusqu’à sa limite saturante obéit
à l’équation d’état des gaz parfaits.
si
on admet que la vapeur sèche jusqu’à sa limite saturante obéit
à l’équation d’état des gaz parfaits.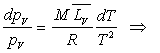 formule
de Dupré si
formule
de Dupré si 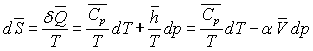 ð
ð  à pression constante
à pression constante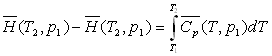 et
et 




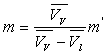 .
.
