CHAPITRE 3 : La variable d'état Température
Plan
1. Principe de Thermométrie (ou
Principe 0 de la Thermodynamique)
2. Echelles de température. Echelle légale
2.1. Thermométrie et grandeur thermométrique
2.2. Faits expérimentaux
2.3. Echelle légale de température
2.4. Autres échelles de température
3. La mesure des températures
3.1. Points fixes fondamentaux
3.2. Les thermomètres
3.3. Thermométrie
" Il fait chaud ", " il fait
froid ", " c’est chaud ", " c’est froid "
... que d’expressions du langage courant pour traduire le fait que la température
fait partie du quotidien humain.
La première notion de température est physiologique, sensitive.
Cependant, nos sensations sont insuffisantes pour établir une échelle
de température et comparer des températures.
L’observation, l’expérience nous apprennent qu’un système se transforme
(par exemple changement de volume) lorsque nos sensations de température
évoluent. Ce constat va nous permettre de préciser quantitativement
le paramètre physique température.
1. Principe de Thermométrie (ou Principe
0 de la Thermodynamique)
Considérons deux corps isolés en état
d’équilibre. Mis en contact thermique entre eux (à ce stade
de nos connaissances en contact physique) ils évoluent vers de nouveaux
états d’équilibre.
Le principe 0 de la Thermodynamique affirme que la variable d’état température
est commune et caractéristique des états d’équilibre atteints.
En d’autres termes et en raisonnant de proche en proche, des systèmes
mis en contact thermique évoluent vers des états d’équilibre
où ils ont même température.
2. Echelles de température. Echelle
légale
2.1. Thermométrie et grandeur thermométrique
La température n’est associée à aucune loi physique, nous pouvons donc choisir des valeurs arbitraires correspondant à des états d’équilibre déterminés. Ainsi la température peut être la valeur d’une grandeur physique (ou une fonction monotone arbitraire de cette grandeur) d’un système à condition d’établir une correspondance bi-univoque entre grandeur physique et température. Par comparaison des états d’équilibre d’autres systèmes avec ceux du système choisi, on mesurera la température des autres systèmes.
Le système choisi est appelé thermomètre, la grandeur physique grandeur thermométrique.
Exemple : le thermomètre est un fil, la grandeur
thermométrique sa longueur.
La longueur dépend de la température puisque, si je " chauffe "
le fil (je change ma sensation de toucher, je conclus que la température
a varié) je constate que la longueur varie.
La température peut être définie soit comme la valeur de
la longueur elle-même, soit comme une fonction monotone arbitraire de
cette longueur.
Il suit que pour rendre la notion de température quantitativement
utilisable par chacun, il a fallu définir une échelle universelle
c’est à dire un thermomètre de référence, une grandeur
thermométrique et une fonction monotone entre cette grandeur et la température.
La définition actuelle de l’échelle légale de température
est le résultat de tâtonnements successifs. C’est pourquoi, de
nos jours, au quotidien, coexistent l’échelle Kelvin, l’échelle
Celsius, l’échelle Farenheit, seule l’échelle Réaumur est
tombée en désuétude.
2.2. Faits expérimentaux
2.2.1. Points fixes
Certains états d’équilibre sont particulièrement
utiles car facilement reproductibles. On les appelle points fixes. Il
s’agit des états d’équilibre de deux phases d’un même corps
pur sous une pression donnée (solide en fusion, liquide en ébullition,
...) ou de trois phases d’un même corps pur ce qui se produit à
une certaine pression (point triple).
Ces états d’équilibre sont facilement reproductibles car indépendants
des masses des phases en présence.
Exemple : la résistance ou la longueur d’un fil de platine immergé dans un mélange de glace et d’eau sous une pression donnée est indépendante des masses d’eau et de glace en présence et reprend toujours la même valeur si on refait le mélange, la pression étant inchangée.
Il est donc très facile de reproduire des températures.
2.2.2. Le gaz parfait, limite de comportement de tous les gaz réels.
Courbes de compressibilité isotherme des gaz
|
|
Les premières expériences de compressibilité
isotherme des gaz, dans des domaines de pression très limités
ne dépassant pas quelques atmosphères, ont été
faites au 17ème siècle par
Mariotte en France et par Boyle en Angleterre.
Plusieurs expérimentateurs (Regnault, Andrews, Cailletet et Amagat)
ont repris ces études au 19ème
siècle dans des domaines de pression de plus en plus élevés.
Kamerlingh Onnes à Leyde a étendu les mesures au domaine
des basses températures.
|
Ces mesures ont été reprises au 20ème
siècle avec une précision accrue sur tous les gaz connus dans
des domaines de température extrêmes et pour des pressions atteignant
1000 atmosphères.
De longues séries de mesures systématiques ont été
faites dans deux laboratoires spécialisés : en Europe celui de
Van Der Waals à Amsterdam sous la direction de Michels et aux Etats -Unis
au laboratoire du Massachusetts Institute of Technology sous la direction de
Beattie.
L’expérience montre que, si l’on trace les courbes de compressibilité
isotherme pour un nombre donné de molécules, pour des pressions
ne dépassant pas quelques atmosphères, on obtient dans un diagramme
p, pV (dit diagramme d’Amagat) les courbes ci-après.
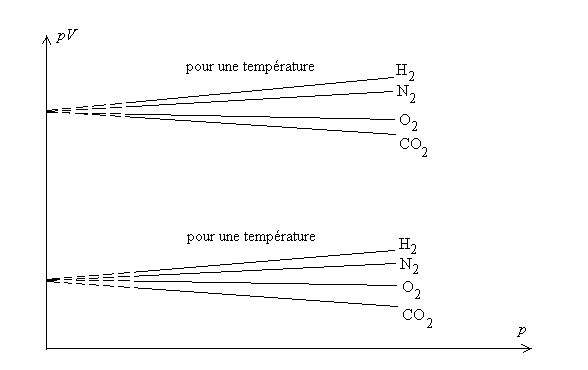
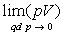 a la même valeur pour une température q
fixée. Cette limite est proportionnelle au nombre de molécules
N ou de moles n (
a la même valeur pour une température q
fixée. Cette limite est proportionnelle au nombre de molécules
N ou de moles n ( où
où  est
le nombre d’Avogadro). Cette limite est indépendante du gaz considéré.
est
le nombre d’Avogadro). Cette limite est indépendante du gaz considéré.
Ainsi  pour tous
les gaz.
pour tous
les gaz.
Définition du gaz parfait : Un gaz qui
aurait, quelle que soit la pression, le comportement de tout gaz réel
à pression nulle est appelée gaz parfait.
Les variables d’état pression p, volume V, température
q et nombre de moles n sont liées
par l’équation d’état 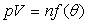
2.3. Echelle légale de température
Le Kelvin : proposé en 1954, adopté en 1967 par le Comité International des Poids et Mesures, le Kelvin est défini de la manière suivante :
- Le thermomètre de référence est le thermomètre à gaz parfait
- La grandeur thermométrique est le produit pV
- La fonction monotone est linéaire soit pV = nRT
où le symbole T est réservé
à la température Kelvin (appelée aussi absolue), où
R est la constante des gaz parfaits.
La valeur de R est déterminée à
partir d’un point fixe de référence (celui de l’équilibre
des trois phases solide, liquide et gazeuse du corps pur H2O
appelé point triple de l’eau). Pour ce point fixe, on a donné
la valeur 273,16 à la température. La mesure de pV à
cette température, pour une mole, par extrapolation jusqu’à la
pression nulle des courbes de compressibilité isotherme des gaz réels
donne 2271,1 joules.
Il suit que R = 2271,1/273,16 = 8,314 MKSA.
La notation symbolique du Kelvin est K.
Remarques :
- pV = nRT (équation liant les variables d’état du gaz parfait) est appelée équation d’état des gaz parfaits.
- Bien que valable en toute rigueur à la pression nulle, cette équation s’applique avec des précisions très satisfaisantes jusqu’à des pressions de quelques atmosphères pour les gaz réels (voir cours sur les équations d'état).
- Historiquement, cette relation fut connue sous le nom de loi de Boyle-Mariotte qui rassemble la loi de Gay-Lussac et la loi de Charles
Loi de Gay-Lussac : à pression constante,
le volume d'un gaz est proportionnel à la température ; à
 .
.
Loi de Charles : à volume constant, la pression
d'un gaz est proportionnelle à la température ;  .
.
Un gaz qui obéit aux lois de Gay-Lussac et de Charles est un gaz parfait (obéit à la loi de Boyle-Mariotte) ð
Démonstration
Loi de Gay-Lussac : à  .
Si on change la valeur de p, cette dernière constante change.
C’est donc une fonction de
.
Si on change la valeur de p, cette dernière constante change.
C’est donc une fonction de 
Loi de Charles : à  .
Si on change la valeur de V, cette dernière constante change.
C’est donc une fonction de
.
Si on change la valeur de V, cette dernière constante change.
C’est donc une fonction de 
En réunissant ces deux résultats, on obtient  .
.
Soit  puisque
la relation doit être vraie quels que soient V et p.
puisque
la relation doit être vraie quels que soient V et p.
 soit
encore pV = CT
soit
encore pV = CT
2.4. Autres échelles de température
Pour les échelles Celsius (notation t), Farenheit
(notation F) et Réaumur (notation R), seule diffère
dans la définition la fonction monotone qui reste linéaire mais
de la forme 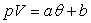 .
.
Les correspondances sont souvent établies de la manière suivante
:
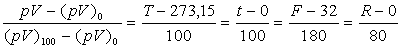
où  correspondent respectivement aux points fixes d’ébullition de l’eau et
de fusion de la glace sous la pression atmosphérique normale, les températures
respectives étant 373,15 K et 273,15 K soient encore 100
°C et 0 °C.
correspondent respectivement aux points fixes d’ébullition de l’eau et
de fusion de la glace sous la pression atmosphérique normale, les températures
respectives étant 373,15 K et 273,15 K soient encore 100
°C et 0 °C.
Il y a une simple translation entre les échelles Celsius et Kelvin (t = T - 273,15).
3. La mesure des températures
Mis à part quelques laboratoires spécialement
équipés, on ne mesure pas une température avec un " thermomètre
à gaz parfait ".
On se sert de thermomètres (et grandeurs thermométriques) que
l’on étalonne, dans la gamme de température d’utilisation, à
partir des valeurs des températures de points fixes déterminées
par ces quelques laboratoires.
3.1. Points fixes fondamentaux
On trouvera ci-après les températures officielles assignées à certains points fixes ; ces valeurs, sauf pour les points triples, correspondent à des états d’équilibre sous la pression atmosphérique normale.
|
ETAT D' EQUILIBRE |
T |
t |
|
Point d'ébullition de l'hélium |
4,2 |
-268,95 |
|
Point triple de l'hydrogène |
13,81 |
-259,34 |
|
Point d'ébullition de l'hydrogène à 33330,6 Pa |
17,04 |
-256,11 |
|
Point d'ébullition de l'hydrogène |
20,28 |
-252,87 |
|
Point d'ébullition du néon |
27,1 |
-246,05 |
|
Point triple de l'oxygène |
54,36 |
-218,79 |
|
Point d'ébullition de l'oxygène |
90,19 |
-182,96 |
|
Point de fusion de l'eau |
273,15 |
0 |
|
Point triple de l'eau |
273,16 |
0,01 |
|
Point d'ébullition de l'eau |
373,15 |
100 |
|
Point de fusion du Zinc |
692,73 |
419,58 |
|
Point de fusion de l'argent |
1235,08 |
961,93 |
|
Point de fusion de l'or |
1337,58 |
1064,43 |
3.2. Les thermomètres
- Le Thermomètre à " gaz parfait "
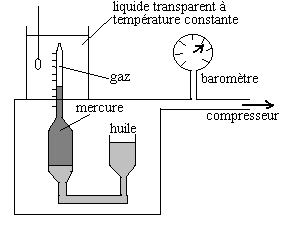
Ce sont les thermomètres de référence. Ils représentent un appareillage important et une technologie poussée pour faire les corrections nécessaires. On fait travailler le " gaz parfait " à volume constant et on étudie ses variations de pression. Le lecteur intéressé pourra se reporter à des ouvrages spécialisés.
- Les thermomètres à dilatation de liquide
Le mercure est le plus performant car :
- il peut être obtenu très pur par distillation
- il ne mouille pas le verre
- il est liquide dans un domaine étendu de température, de -39
°C à 360 °C
- sa conductivité thermique est très bonne, par suite il se met
rapidement en équilibre thermique avec le corps en contact
- sa capacité calorifique est faible (O,5 cal/cm3
.°C) est à peu près égale à celle du verre.
Les thermomètres à liquide comprennent un réservoir
dont le volume n’excède pas 1 cm3
soudé à une tige capillaire de diamètre intérieur
de quelques dixièmes de millimètre. La paroi est mince pour permettre
l’établissement rapide de l’équilibre thermique.
Avec une bonne approximation, on peut considérer que le volume V
du liquide dans le thermomètre varie avec la température suivant
la relation : 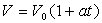
Pour le mercure dans le verre, on prend pour a la valeur moyenne 1/6300.
Au-dessous de -39 °C, on utilise l’éthanol jusqu’à -80
°C, le toluène jusqu’à -90 °C, le pentane jusqu’à
-200 °C.
Au-dessus de 500 °C, le gallium permet d’atteindre 1000 °C.
- Les thermomètres à tension de vapeur saturante
La vapeur d’un corps en équilibre avec son liquide est
dite saturante. Sa pression  n’est fonction que de la température. Parmi les diverses expressions
utilisées pour représenter
n’est fonction que de la température. Parmi les diverses expressions
utilisées pour représenter  ,
on adopte souvent celle du type
,
on adopte souvent celle du type  .
.
Ces thermomètres sont utilisés aux basses températures
avec des gaz comme  pour lesquels les variations de
pour lesquels les variations de  avec T sont considérables.
avec T sont considérables.
|
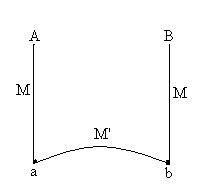
|
Trois fils constitués de deux métaux ou
alliages différents M et M’ sont soudés (ou en contact)
en a et b où règnent des températures  .
Il apparaît en A et B une force électromotrice e fonction
de l’écart de températures. .
Il apparaît en A et B une force électromotrice e fonction
de l’écart de températures.
Des relations de type  sont utilisées pour déterminer l’écart de température.
sont utilisées pour déterminer l’écart de température.
Leur domaine d’utilisation varie entre -180 et 2500 °C.
|
- Les thermomètres à résistance
On utilise le fait que la résistance électrique
d’un fil métallique dépend de la température. On mesure
sa résistance par exemple par la méthode du pont de Wheastone.
La température est le plus souvent définie par des relations du
type 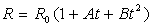 .
.
Les métaux utilisés sont principalement, le platine pour des températures
comprises entre -183 et 630 °C, le cuivre pour des températures
inférieures à 150 °C, le nickel pour des températures
comprises entre 0 et 150 °C.
La résistance d’un échantillon semi-conducteur
est très sensible à la température. On utilise des thermistances
pour mesurer de très faibles variations de température suivant
des relations de type 
- Les thermomètres à quartz
La fréquence de résonance d’un quartz piézoélectrique varie avec la température. Le domaine d’utilisation est entre -200 et 600 °C.
Ils sont utilisés aux températures très
élevées.
Leur fonctionnement fait appel aux lois du rayonnement thermique (hors programme).
- Les très basses températures (quelques mK)
Ces très basses températures s’obtiennent en
faisant subir à un sel paramagnétique une magnétisation
isotherme puis une désaimantation adiabatique.
Après l’opération décrite la température du sel
évolue de  suivant la formule
suivant la formule
 où
H est le champ magnétique,
où
H est le champ magnétique,  la perméabilité magnétique du vide, C la constante
de Curie, c la vitesse de la lumière dans le vide et s
la constante de Stéfan-Boltzmann.
la perméabilité magnétique du vide, C la constante
de Curie, c la vitesse de la lumière dans le vide et s
la constante de Stéfan-Boltzmann.
3.3. Thermométrie
Mesurer une température s’avère souvent difficile
; en effet, faire un étalonnage précis d’un thermomètre
soulève des problèmes, introduire le thermomètre à
l’endroit où l’on veut connaître la température perturbe,
parfois notablement, la température.
Nous n’en dirons pas plus dans le cadre de ce cours.




 où
H est le champ magnétique,
où
H est le champ magnétique,