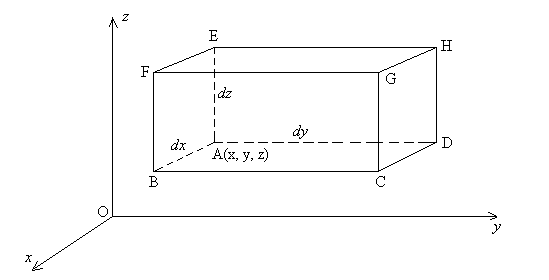CHAPITRE 2 : La variable d'état Pression
Plan
1. Pression dans un fluide au repos (en
équilibre dans un référentiel galiléen)
1.1. Etude expérimentale dans le champ de pesanteur
1.2. Définition de la pression dans un fluide
1.3. Remarque
1.4. Relation locale traduisant l’équilibre d’un
fluide dans un référentiel galiléen
2. Cas d’un fluide au repos dans un référentiel
galiléen soumis au champ de pesanteur. Principe de l’hydrostatique.
2.1. Surface de séparation entre deux fluides non
miscibles au repos
2.2. Fluide incompressible (liquide)
2.3. Fluide compressible (gaz)
1. Pression dans un fluide au repos (en équilibre dans un référentiel galiléen)
Notre sens commun nous fait appréhender un fluide (gaz ou liquide) comme étant de nature très différente d’un solide. Ce dernier a une forme propre qui nous permet de le reconnaître. Liquide ou gaz n’ont pas de forme propre, ils épousent la forme du récipient qui les contient, sont déformables sous la moindre action. Liquide et gaz ont des différences : un liquide, contrairement à un gaz, a un volume défini, il ne remplit pas tout le volume du récipient.
1.1. Etude expérimentale dans le champ de pesanteur
|
|
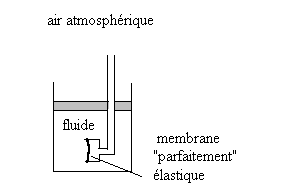
Le tube en U avec la membrane élastique est placé dans l’air atmosphérique : la membrane n’est pas tendue. Nous plaçons l’extrémité avec membrane dans un liquide (ou dans un gaz dont on peut faire varier le volume à l’aide d’un piston) : la membrane élastique est tendue comme indiqué sur la figure ; ceci traduit des efforts du fluide sur la membrane |
La forme de la membrane est indépendante de l’orientation
de la membrane autour d’un même point, les efforts sur la membrane sont
perpendiculaires à celle-ci.
Si le fluide est un liquide, la déformation de la membrane augmente de
manière significative avec la profondeur.
Autre expérience : si, dans un récipient contenant un liquide, nous perçons un trou, l’écoulement de liquide se produit perpendiculairement à l’orifice quelque soit l’orientation de ce dernier.
1.2. Définition de la pression dans un fluide
|
|
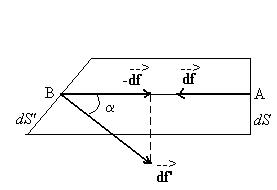
Considérons un fluide en équilibre dans un référentiel lié au sol supposé galiléen et une portion de ce fluide limitée extérieurement par un cylindre élémentaire de révolution d’axe AB horizontal et dont les bases sont, en A une section droite dS, en B la surface plane dS’ dont la normale fait un angle a avec l’axe AB. Nous avons |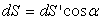
Cette portion de fluide n’est pas soumise qu’à son seul
poids (voire à d’autres forces dues à un champ extérieur)
pour être en équilibre. Elle est soumise à des forces " superficielles "
(sur les surfaces délimitant le cylindre) dues au fluide extérieure
environnant la portion, les forces internes à la portion n’interviennent
pas car elles obéissent au principe de l’action et de la réaction.
Les forces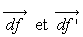 
exercées
par le fluide environnant sur les bases (non matérielles) dS et dS’ du
volume élémentaire de fluide sont normales à celles-ci
(sinon il y aurait glissement entre les couches du fluide puisqu’un fluide se
déforme à la moindre action extérieure).
La condition d’équilibre sur l’axe horizontal se traduit par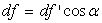 
.
Soit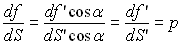 
qui, par définition, est la pression dans le fluide.
La pression p en un point d’un fluide en équilibre est indépendante de l’orientation de l’élément de surface qui sert à la définir.
La pression est une grandeur scalaire positive, la force de pression est une grandeur vectorielle.
La pression est la même en tous les points d’un plan horizontal pris dans un fluide en équilibre.
La notion de pression n'a de sens que dans un fluide. En effet les forces de pression s'exercent perpendiculairement à tout élément de surface parce qu'un fluide se déforme sous le moindre effort.
Pour un solide, le problème est plus complexe car un solide résiste aux efforts qu'on exerce dessus : il faut alors parler de forces de contraintes exercées sur les faces de tout élément volumique d'un solide.
1.4. Relation locale traduisant l’équilibre d’un fluide dans un référentiel galiléen
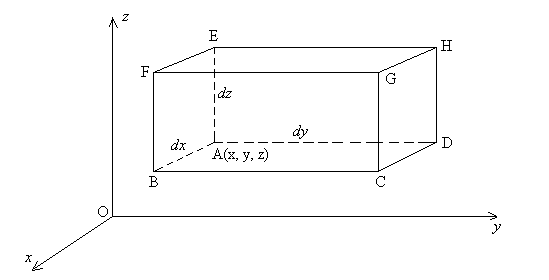
Exprimons la relation d’équilibre pour un élément
de fluide en forme de parallélépipède rectangle de dimensions
dx, dy et dz à partir du point A de coordonnées
x, y et z.
Sur la surface rectangulaire ABFE, nous avons une pression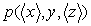 
et, sur la surface rectangulaire DCGH, nous avons une pression 
.
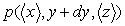Il en est de même sur les autres faces du parallélépipède
rectangle en permutant les coordonnées. Les forces dues à des
champs de forces extérieures s’écrivent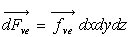 
.
En appliquant les relations d’équilibre de la Mécanique et en
projetant suivant la direction Oy, on obtient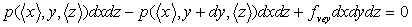 
.
Soit encore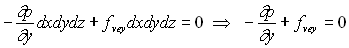 
; 
;
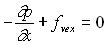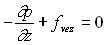
Sous forme vectorielle, ces trois dernières relations
s’écrivent :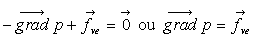 
Remarque : le gradient de pression n’est due qu’aux champs de forces extérieures.
2. Cas d’un fluide au repos dans un référentiel galiléen soumis au champ de pesanteur. Principe de l’hydrostatique.
Le fluide a pour masse volumique m
et le champ de pesanteur est le seul champ de forces extérieures.
Dans ce cas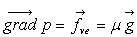 
relation équivalente à 
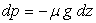si l’axe 
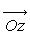est vertical
ascendant. Ceci constitue le principe de l’hydrostatique.
Remarque sémantique : nous avons employé le mot "Principe" pour traduire une relation (démontrée à partir du principe fondamental de la Mécanique) ; nous aurions du dire Théorème ; en fait, cela se produit souvent en Physique : ce qui était un Principe à une époque devient un Théorème avec l'avancement des connaissances et, souvent, à tort, on garde la première terminologie.
Autre démonstration :
|
|
Dans le champ de pesanteur, on considère une tranche
de fluide à l'altitude z d'épaisseur |
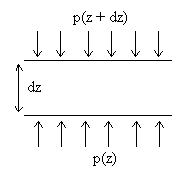
L’augmentation de pression entre une altitude z + dz
et une altitude z est due au poids du fluide dans le cylindre de hauteur
verticale dz et de surface horizontale unitaire.
L’évolution de pression est donc continue, même à la séparation
de deux fluides.
La pression a une altitude z est égale au poids, par unité
de surface horizontale, des couches de fluide situées à la verticale
au-dessus de z.
Dans un même fluide au repos, les surfaces d’égale altitude sont
isobares (même pression).
Dans le système MKSA, les pressions se mesurent en N m-2
que l’on appelle Pascal (Pa).
Attention, il ne faudrait
pas conclure que les forces de pression s’exercent verticalement. Elles s’exercent
perpendiculairement à tout élément de surface.
2.1. Surface de séparation entre deux fluides non miscibles au repos
Considérons deux points de cette surface. Soit dz
leur différence d’altitude.
On peut écrire, en négligeant toute discontinuité de la
pression à la traversée de la surface de séparation :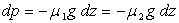
ce qui entraîne dz = 0.
La surface de séparation entre deux fluides non miscibles au repos est plane et horizontale.
L’étude de la stabilité de l’équilibre montrerait que le liquide de densité plus faible se place au dessus de celui de densité plus forte.
2.2. Fluide incompressible (liquide)
La masse volumique est constante et l’intégration du
principe de l’hydrostatique donne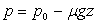 
.
Cette relation est souvent appelée principe de Pascal
Applications : baromètre - presse hydraulique
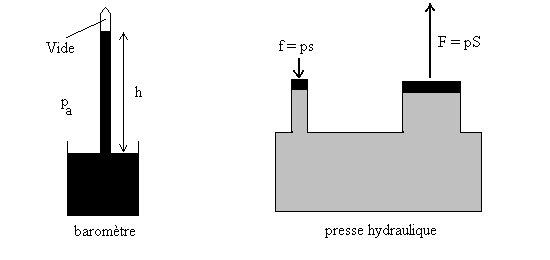
Dans un baromètre à mercure, pour une pression
atmosphérique normale, la hauteur h est égale à 760 mm
ce qui correspond à :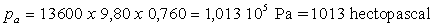
Souvent, les pressions sont exprimées en mm de mercure, en atmosphère
(1 atm correspond à la pression atmosphérique normale), en bar
(1 bar = 105 Pa) ou millibar (mbar).
Nous remarquerons que pour une hauteur d’eau de 3m, la variation de pression
est égale à 30000 Pa soit à peu près le tiers de
la pression atmosphérique normale.
A l’échelle humaine courante, les variations de pression sont sensibles dans les liquides.
Un baromètre mesure une pression absolue puisque la pression dans le vide est nulle (pas de masse = pas de poids). Les manomètres qui mesurent les différences de pression seront étudiés en Travaux dirigés et pratiques.
2.3. Fluide compressible (gaz)
La masse volumique dépend de la pression et nous le
verrons de la température. On ne peut intégrer directement
la relation dp = -m g dz.
Cependant les masses volumiques des gaz sont faibles (air dans les conditions
courantes 1,3 Kg m-3) et, à
l’échelle humaine courante, on négligera les variations de pression
avec l’altitude dans les gaz.
Seul l’air atmosphérique présente
des différences d’altitude suffisantes pour ne pas négliger les
variations de pression (il faut compter de l'ordre de 1 km d'altitude
pour que les variations de pression deviennent significatives).
.
en équilibre dans un référentiel lié au sol
supposé galiléen.
la masse volumique du fluide, 
et
les intensités
par unité de surface des forces extérieures qui s'exercent
sur les bords de la tranche.
.