CHAPITRE 6 : Notions simples sur les systèmes
ouverts. Application à l’écoulement des fluides
Plan
1. Premier principe de la Thermodynamique pour un système
ouvert
2. Application à l’écoulement des fluides
2.1. Description du fluide en mouvement
2.2. Bilan énergétique
2.3. Théorème d’Euler. Résultante des
forces sur un fluide
1. Premier principe de la Thermodynamique
pour un système ouvert
 |
Outre les échanges d’énergie sous
forme travail des forces d’opérateurs extérieurs et sous
forme de chaleur, nous avons noté qu’un système échange
de l’énergie par transferts de matière.
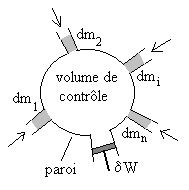
Le système (appelé aussi volume de contrôle lorsqu’il
y a échange de matière) est " augmenté " entre les
instants t et t+dt des masses dmi
(grisées sur le dessin ci-contre) contenues dans les conduites.
Les masses dmi ont un caractère
algébrique, positives si elles entrent effectivement dans le volume
de contrôle, négatives si elles en sortent. |
Nous appelons  l’énergie massique de la matière échangée par la
conduite i et
l’énergie massique de la matière échangée par la
conduite i et  son
volume massique.
son
volume massique.
La variation d’énergie dE du volume de contrôle
entre les instants t et t+dt est égale à :

Le travail  est constitué du travail d W
(*) échangé par le système au niveau des
parois mobiles (type piston) et du travail du milieu extérieur pour faire
" entrer " les masses dmi dans le système.
est constitué du travail d W
(*) échangé par le système au niveau des
parois mobiles (type piston) et du travail du milieu extérieur pour faire
" entrer " les masses dmi dans le système.
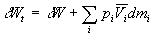 où pi
est la pression de la matière de masse dmi
" entrant " par la conduite i et
où pi
est la pression de la matière de masse dmi
" entrant " par la conduite i et  son volume.
son volume.
Ainsi :



Cette relation constitue l’expression du premier principe de la Thermodynamique
pour un système ouvert.
On y notera l’introduction naturelle de la fonction d’état enthalpie.
Remarques :
- (*) La plupart des auteurs appellent " travail utile ou technique" ce travail
et le notent d Wu
ou d W* .
Nous avons gardé la notation d W mais
il faut bien comprendre que c’est le travail échangé sur l’arbre
de la machine,
- La démonstration de la relation du premier principe de la Thermodynamique
pour un système ouvert aurait pu être faite en considérant à l'instant t
un système fermé constitué du volume de contrôle et des masses entrantes pendant
le temps dt devenu à l'instant t + dt un systéme fermé
constitué du volume de contrôle et des masses sortantes pendant l'instant dt.
Exemples d’utilisation
En limitant nos propos aux régimes permanents c’est à
dire à des systèmes qui " n’accumulent " ni énergie,
ni matière.
 soit,
soit, 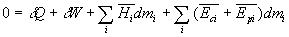
et aux cas de deux conduites, l’une par laquelle la matière
entre, l’autre par laquelle elle sort
(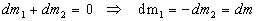 ),
),
on obtient : 
Utilisation 1 : L’énergie mécanique est constante
ou les variations d’énergie mécanique sont négligeables
devant les variations d’enthalpie.
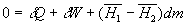
- Le système n’échange ni travail (d
W = 0) ni chaleur (d Q = 0)
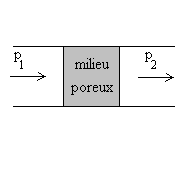 |
C’est le cas d’un écoulement à
travers un milieu poreux sans énergie mécanique significative
avec p1 > p2.
C’est la détente de Joule-Thomson.

|
- Le système n’échange que du travail (d
Q = 0)
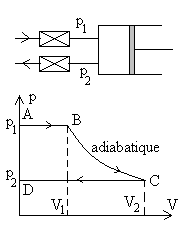 |
C’est le cas d’un cylindre moteur (sens ABCD) ou d’un
compresseur (sens DCBA). Le cycle pour un cylindre moteur est constitué
de la phase entrée de matière AB, de la phase détente
BC, de la phase sortie de matière CD, si bien que le travail est 
En remarquant que  suivant une adiabatique, on peut écrire
suivant une adiabatique, on peut écrire  qui constitue l’expression du travail avec transvasement.
qui constitue l’expression du travail avec transvasement. |
La durée dt d’un cycle est faible, nous raisonnons pour une quantité
élémentaire de travail échangé et pour une masse
dm de matière si bien que 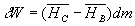 ð
ð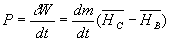
P est la puissance motrice du cylindre moteur et  le débit massique.
le débit massique.
Pour un compresseur, on aura 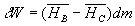 ou
ou 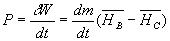
- Le système n’échange que de la chaleur (d
W = 0)
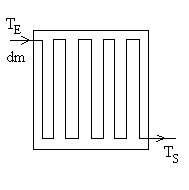 |
C’est le cas des échangeurs de chaleur,
radiateurs, évaporateurs, condenseurs.
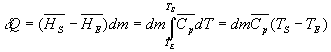 pour un écoulement
à pression constante en considérant pour un écoulement
à pression constante en considérant 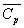 constant dans l’intervalle de température considéré.
constant dans l’intervalle de température considéré.
Par unité de temps,
 où où  est le flux de chaleur échangé
est le flux de chaleur échangé |
Utilisation 2 : Les échanges de chaleur et de travail
sont nuls.
 C’est le cas
de l’écoulement des fluides non visqueux que nous allons étudier
avec plus de précisions dans le paragraphe suivant.
C’est le cas
de l’écoulement des fluides non visqueux que nous allons étudier
avec plus de précisions dans le paragraphe suivant.
2. Application à l’écoulement
des fluides
2.1. Description d’un fluide en mouvement
Il s’agit de déterminer, en chaque lieu et à tout instant, la
vitesse des particules du fluide, c’est à dire le champ de vitesses  .
.
On appelle :
- lignes de courant (ou d’écoulement), les courbes tangentes
au vecteur vitesse à un instant donné,
- tube de courant, un ensemble des lignes de courant s’appuyant
sur un contour fermé,
- trajectoire d’une particule, la courbe suivie par la particule,
- ligne d’émission, la courbe formée, à
un instant donné, par l’ensemble des particules passées en
un même point.
Nous limitons nos propos à des écoulements en régime
permanent (stationnaire), le vecteur vitesse ne dépend pas du
temps, les lignes de courant et les tubes de courant sont stables.
Dans ce cas, ligne de courant, trajectoire et ligne d’émission
sont confondues.
Il ne faut cependant pas conclure qu’une particule du fluide n’a pas
d’accélération. En effet lorsque au cours du temps, elle
se déplace d’un point à un autre, elle change, a priori,
de vitesse et a donc une accélération.
Ceci précisé, ce cours n’a pas pour objet la cinématique
des fluides.
2.2. Bilan énergétique
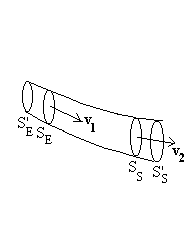 |
Isolons un tube de courant suffisamment étroit
(filet) pour que la pression et la vitesse d’écoulement puissent
être considérées uniformes sur toute section droite.
Le système est le fluide de masse M entre les sections droites SE
et SS . En régime stationnaire la
forme du système est invariante.
Entre les instants t et t + dt, la masse dm qui entre
à vitesse 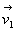 est
contenue entre les sections droites S’E
et SE . Elle est égale à
la masse qui sort (conservation de la masse due à l’hypothèse
de régime stationnaire) à vitesse est
contenue entre les sections droites S’E
et SE . Elle est égale à
la masse qui sort (conservation de la masse due à l’hypothèse
de régime stationnaire) à vitesse 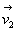 contenue
entre les sections droites SS et S’S. contenue
entre les sections droites SS et S’S. |
Un fluide (surtout les gaz) est peu conducteur de la chaleur et nous
négligeons les transferts d’énergie thermique.
Nous négligeons toute viscosité du fluide si bien
qu’il n’y a pas de perte d’énergie mécanique par frottement
entre deux tubes de courant adjacents.
Le premier principe pour un système ouvert s’écrira : 
soit aussi 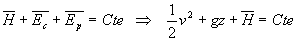 en nous limitant à de l’énergie potentielle due au champ de pesanteur.
en nous limitant à de l’énergie potentielle due au champ de pesanteur.
Cette relation est l’équation de bilan énergétique.
Dans le cas des écoulements " irrotationnels c’est à dire
sans tourbillon ", on montre que la valeur de la constante est indépendante
du tube de courant.
Pour comprendre cette notion d’écoulement irrotationnel, il
nous faudrait disposer de connaissances réelles de cinématique
des fluides et, en particulier, de l’équation d’Euler.
Fluides incompressibles non visqueux
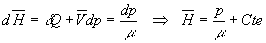 puisque la
masse volumique m est constante
puisque la
masse volumique m est constante
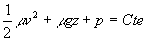 qui est connu
sous le nom d’équation de Bernoulli.
qui est connu
sous le nom d’équation de Bernoulli.
Remarque : l’établissement de l’équation de bilan
énergétique a été faite pour un filet de fluide
où on peut considérer que pression, vitesse et énergie
potentielle sont uniformes sur toute section droite du filet ; on notera
que, pour la surface plane d’un liquide au contact avec un gaz, ces conditions
sont remplies, cette surface n’étant pas de dimensions faibles.
Fluides compressibles non visqueux
Nous nous limitons aux gaz parfaits pour lesquels 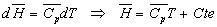
La relation de Bernoulli devient 
Elle prend le nom d’équation de Saint Venant.
Pour la résolution, il faut adjoindre l’équation d’état
des gaz parfaits 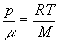 et l’équation d’isentropicité
et l’équation d’isentropicité 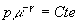 .
.
Fluides visqueux
Pour maintenir le fluide visqueux en écoulement stationnaire,
il faut lui fournir la puissance mécanique P dissipée par
frottement visqueux.
On introduit la perte de charge 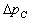 (dans les livres, pour un certain nombre de cas, on trouve des valeurs de perte
de charge) par la relation :
(dans les livres, pour un certain nombre de cas, on trouve des valeurs de perte
de charge) par la relation : 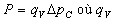 est
le débit volumique du fluide.
est
le débit volumique du fluide.
Présence d’une machine hydraulique dans l’écoulement
 |
Il faut tenir compte de l’énergie mécanique
fournie (pompe à eau, ventilateur à air) ou absorbée
(aube à eau, turbine à gaz) par la machine.
Pour un écoulement de fluide non visqueux :
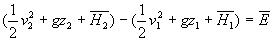
où 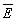 est l’énergie massique de la machine. Elle est positive pour une
pompe, négative pour une turbine.
est l’énergie massique de la machine. Elle est positive pour une
pompe, négative pour une turbine. |
2.3. Théorème d’Euler. Résultante
des forces sur un fluide
Nous reprenons le schéma du tube de courant.
La masse M+dm à l’instant t a une quantité de mouvement
: 
La masse M+dm à l’instant t+dt a une quantité de
mouvement : 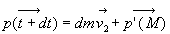
Ainsi 
Le principe fondamental de la dynamique permet d’écrire :
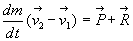 où
où 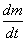 est le débit massique du fluide,
est le débit massique du fluide,  est le poids de fluide considéré (si on se limite à des
forces de volume de pesanteur) et
est le poids de fluide considéré (si on se limite à des
forces de volume de pesanteur) et  l’action sur la portion de fluide considérée des éléments
en contact avec celle-ci (forces de pression si on ne considère pas les
efforts de viscosité).
l’action sur la portion de fluide considérée des éléments
en contact avec celle-ci (forces de pression si on ne considère pas les
efforts de viscosité).
Pour un volume de contrôle où S est la surface fermée
le délimitant, le débit massique sortant par un élément  est égal à
est égal à 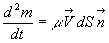 .
.
Pour ce débit massique, le " débit " de quantité de mouvement
est égal à 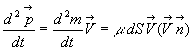 .
.
En intégrant au volume de contrôle, on obtient le théorème
d’Euler 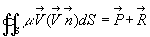 .
.
En utilisant le principe de l’action et de la réaction, on accède
simplement à l’action du fluide sur les parois en contact.




 qui constitue l’expression du travail avec transvasement.
qui constitue l’expression du travail avec transvasement.
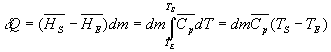 pour un écoulement
à pression constante en considérant
pour un écoulement
à pression constante en considérant 


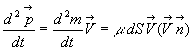 .
.