Le gaz est aspiré à () et refoulé à .

1) Représenter dans un diagramme (p, V) et dans un diagramme (T, S) les phases aspiration, compression et refoulement.
Justifier la relation où les quantités sont respectivement la variation massique d’enthalpie , la quantité de chaleur massique échangée par le gaz avec l’extérieur et le travail massique échangé avec transvasement.

2) Le cylindre compresseur est dit " idéal " si la transformation de compression est isentropique.
Trouver une relation entre volume V, pression p et .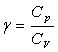
Calculer le travail et la variation d’enthalpie pour l’unité de masse de gaz traversant le cylindre compresseur.
Etudier le signe de ces quantités.

3) La transformation de compression n’est pas réversible car on ne peut négliger les frottements internes du gaz.
Pour tenir compte de ceux-ci, on introduit une évolution " fictive " réversible, non adiabatique telle que . On pose où a est une constante.
Trouver une relation, de même forme qu’en 2), entre volume V, pression p et un coefficient k que l’on calculera en fonction de a et . Comparer k et suivant les valeurs possibles de a.
Calculer le travail pour l’unité de masse de gaz traversant le cylindre compresseur.
Comparer les travaux pour le cylindre compresseur " idéal " et le cylindre compresseur " réel ". En déduire le rendement isentropique.

| Méthodologie | Réponse 1) | Réponse 2) | Réponse 3) |

Le gaz est aspiré à () et refoulé à .

1) Représenter dans un diagramme (p, V) et dans un diagramme (T, S) les phases aspiration, détente et refoulement.
Justifier la relation où les quantités sont respectivement la variation massique d’enthalpie , la quantité de chaleur massique échangée par le gaz avec l’extérieur et le travail massique échangé avec transvasement.

2) Le cylindre moteur est dit " idéal " si la transformation de détente est isentropique.
Trouver une relation entre volume V, pression p et .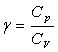
Calculer le travail et la variation d’enthalpie pour l’unité de masse de gaz traversant le cylindre moteur.
Etudier le signe de ces quantités.

3) La transformation de détente n’est pas réversible car on ne peut négliger les frottements internes du gaz.
Pour tenir compte de ceux-ci, on introduit une évolution " fictive " réversible, non adiabatique telle que . On pose où a est une constante.
Trouver une relation, de même forme qu’en 2), entre volume V, pression p et un coefficient k que l’on calculera en fonction de a et . Comparer k et suivant les valeurs possibles de a.
Calculer le travail pour l’unité de masse de gaz traversant le cylindre moteur.
Comparer les travaux pour le cylindre moteur " idéal " et le cylindre moteur " réel ". En déduire le rendement isentropique.

| Méthodologie | Réponse 1) | Réponse 2) | Réponse 3) |

Le gaz est aspiré à () et refoulé à .

1) Pour une transformation de compression ou de détente, justifier la relation où les quantités sont respectivement la variation massique d’enthalpie , la quantité de chaleur massique échangée par le gaz avec l’extérieur et le travail massique échangé à l’arbre de la turbomachine.

2) La turbomachine est dite idéale si la transformation de compression ou de détente est réversible.
Trouver une relation entre volume V, pression p et .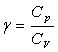
Calculer le travail et la variation d’enthalpie pour l’unité de masse de gaz traversant la turbomachine.
Etudier le signe de ces quantités pour la compression, puis pour la détente.

3) La transformation de compression ou de détente n’est plus réversible car on ne peut négliger les frottements internes du gaz.
Pour tenir compte de ceux-ci, on introduit une évolution " fictive " réversible, non adiabatique telle que . On pose où a est une constante pour la turbomachine considérée.
Trouver une relation, de même forme qu’en 2), entre volume V, pression p et un coefficient k que l’on calculera en fonction de a et . Comparer k et suivant les valeurs possibles de a.
Calculer le travail pour l’unité de masse de gaz traversant la turbomachine.
Comparer les travaux pour la turbomachine " idéale " et la turbomachine " réelle " pour la compression et la détente . En déduire dans chacun de ces cas le rendement isentropique.

| Méthodologie | Réponse 1) | Réponse 2) | Réponse 3) |

1) On se propose d’exprimer les variations élémentaires d’enthalpie massique et d’entropie massique d’un corps pur en fonction des variations de température et de pression .
Pour les fluides réels, la variation d’entropie massique s’écrit : où est le coefficient de dilatation isobare.
En déduire l’expression de .
Pour l’eau, on supposera constantes dans le domaine d’application du problème les données suivantes :  ;  ;

2) Une pompe idéale fonctionne de manière isentropique. Elle aspire de l’eau à sous une pression . Elle la refoule sous une pression .
Calculer le travail massique de compression à fournir sur l’arbre de la pompe (dit travail utile avec transvasement) et la variation de température de l’eau à la traversée de la pompe.

3) Pour une pompe réelle fonctionnant dans les mêmes conditions d’aspiration () et de refoulement (), on peut conserver l’hypothèse d’un fonctionnement adiabatique mais on ne peut négliger les frottements fluides internes.
On définit alors le rendement isentropique 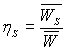où est le travail massique réel à fournir à l’arbre de la pompe.
Si l’on a mesuré une élévation de température de l’eau à la traversée de la pompe, calculer la variation d’entropie massique , le travail massique de compression et le rendement isentropique de la pompe.

| Méthodologie | Réponse 1) | Réponse 2) | Réponse 3) |

5 - Un récipient a une symétrie de révolution autour de l’axe vertical 0z. Le rayon r durécipient à la cote z est donné par .

de l’eau à un instant t .

2)1) Comparer à l’instant t , pour une surface de l’eau de cote z toujours très supérieure à la section s de l’orifice, vitesse v(z) du niveau d’eau à la cote z et vitesse d’éjection.
2)2) En déduire que et que l’équation différentielle donnant la hauteur d’eau est .

3)1) Déterminer les coefficients n et a pour que le niveau d’eau du récipient baisse régulièrement de 6 cm par minute.
3)2) Quelle est la hauteur minimale z = h d’eau dans le récipient pour que .

4) Quel volume d’eau doit-on mettre dans le récipient pour que le temps d’écoulement de l’eau entre la hauteur H et la hauteur h soit de 15 minutes ? Quelle a pu être l’utilité de cet appareil ?

| Méthodologie | Réponse 1) | Réponse 2)1) | Réponse 2)2) | Réponse 3)1) | Réponse 3)2) | Réponse 4) |

1) Calculer la vitesse d’éjection initiale de l’eau par l’orifice.

2) Pendant l’écoulement de l’eau, l’air au-dessus de l’eau se détend. Calculer la vitesse d’éjection de l’eau lorsque la surpression de l’air par rapport à est réduite de moitié.

3) Déterminer l’équation du second degré en h, où h désigne la hauteur d’eau qui reste dans le réservoir au moment où l’eau cesse de s’écouler. Calculer h.

4) Quelle aurait dû être la cote du trou pour que la portée du jet d’eau initial soit maximale ? Calculer cette portée et la vitesse d’éjection correspondante.

| Méthodologie | Réponse 1) | Réponse 2) | Réponse 3) | Réponse 4) |

2) En faisant l’hypothèse que l’eau est un fluide parfait, calculer la différence de pression entre les points . En déduire le sens de la dénivellation de mercure dans le tube en U.

3) Calculer le débit d’eau, en déduire la vitesse à l’arrivée sur le convergent.

| Méthodologie | Réponse 1) | Réponse 2) | Réponse 3) |

| Méthodologie | Réponse 1) | Réponse 2) | Réponse 3) |