CHAPITRE 1 : Généralités sur la Thermodynamique. Statique des fluides. Thermométrie. Gaz parfait.

Plan

1. Physique des milieux continus et Thermodynamique
1.1. Systèmes. Variables d’état. Etat d’équilibre. Equations d’état
1.2. Transformations d’un système
2. Statique des fluides
2.1. Pression dans un fluide au repos
2.2. Cas d’un fluide au repos dans un champ de pesanteur
2.3. Relation locale dans un référentiel non galiléen
2.4. Phénomènes de tension superficielle
3. Température et équation d’état des gaz parfaits
3.1. Principe de Thermométrie
3.2. Echelles de température. Echelle légale
3.3. La mesure des températures
4. Applications simples de l’équation d’état des gaz parfaits
4.1. Un gaz parfait obéit aux lois de Gay-Lussac et de Charles
4.2. Un gaz qui obéit aux lois de Gay-Lussac et de Charles est un gaz parfait
4.3. Mélange idéal de gaz parfaits
4.4. Autre écriture de l’équation d’état des gaz parfaits
4.5. Masse volumique et densité des gaz parfaits

1. Physique des milieux continus et Thermodynamique

Parce que l’enseignement des notions d’atomistique est largement développé, chacun est convaincu du caractère discontinu de la matière. Pourtant à l’échelle macroscopique courante, la matière nous parait continue. Ces deux façons d’appréhender la matière sont complémentaires, se nourrissent l’une de l’autre tout au long de l’enseignement des Sciences Physiques.
Les deux premiers chapitres de ce cours seront consacrés à l’étude de modèles simples qui nous permettent de rendre compte scientifiquement de la matière.
La Physique ne s’est pas faite en un jour, elle est le résultat de tâtonnements successifs, un cours (surtout celui que nous allons faire dans ces deux chapitres) n’est jamais linéaire. Il arrive souvent que l’on soit amené à faire appel au sens commun pour présenter une notion, un modèle qui, de fait, nous sert à définir, à qualifier, à quantifier le phénomène …donc à le comprendre.

Macroscopiquement aussi petit soit-il, un échantillon de matière, en Physique des milieux continus, contient un grand nombre de particules - 3 cm³ d’eau renferme molécules - . L’hypothèse de milieu continu considère que la matière occupe continûment tout le volume. Ainsi si un échantillon de volume dV contient des particules, la masse dm de l’échantillon sera la somme des masses des particules et, en Physique des milieux continus, on définit la masse volumique  qui a donc un caractère de valeur moyenne.

1.1. Systèmes. Variables d’état. Etat d’équilibre. Equations d’état.

Nous appelons système un ensemble constitué d’un grand nombre de particules. Tout système sera en interaction avec d’autres systèmes de l’Univers qui constituent le milieu extérieur.
L’interaction se traduit par des échanges de matière et des échanges d’énergie sous forme de travail et de chaleur.
Système et milieu extérieur peuvent ne pas présenter de différences de nature, mais l’observateur les différencie par le rôle qu’il leur fait jouer, les frontières les séparant pouvant être réelles ou fictives.
Un système est fermé s’il ne peut échanger de la matière avec l’extérieur, dans le cas inverse il est ouvert.
Un système fermé est isolé s’il n’échange aucune énergie avec l’extérieur, il n’est pas isolé s’il échange de l’énergie.

En Physique des milieux continus, on décrit l’état d’un système par l’introduction d’un nombre restreint de paramètres mesurables qui rendent compte de l’état du système. On les appelle variables d’état.
C’est l’expérience qui est déterminante pour définir les variables d’état nécessaires.
La température, la pression, le volume et la quantité de matière sont les variables d’état les plus couramment nécessaires. Ce ne sont pas les seules mais, sauf cas très exceptionnel, nous n’envisagerons que ces seules variables d’état dans le cadre de ce cours où on s’intéresse principalement aux fluides et en particulier aux gaz.

Un système est en état d’équilibre si les variables d’état du système sont constantes (dans le temps) et uniformes dans toute partie homogène du système.
Pour mieux comprendre : Soit le mur extérieur d’une maison chauffée. Sa température varie d’un endroit à un autre du mur, de la température intérieure à celle extérieure. Le système " mur " est en état de déséquilibre même si, en chaque endroit, la température est constante. Dans ce dernier cas, on dira que le mur est en régime permanent. Si la température évoluait au cours du temps, le mur serait en régime transitoire.
Dans un système en état d’équilibre, on appelle équation d’état toute relation entre les variables d’état.

En Physique des milieux continus, la Thermodynamique est définie comme la science qui étudie les phénomènes où intervient la température. Elle est née vers les années 1820, au début de l’ère industrielle, de la nécessité de connaître, sur les machines thermiques construites, la relation entre les phénomènes thermiques et les phénomènes dynamiques, d’où son nom.

1.2. Transformations d’un système

Dans une transformation il y a variation d’au moins une variable d’état du système qui évolue d’un état initial à un état final. Sauf pour les systèmes fermés, isolés où il y a transformation spontanée du système vers un état d’équilibre si celui-ci n’était pas en état d’équilibre, la transformation se produit par l’action du milieu extérieur.
Pour que la transformation puisse être définie convenablement, il conviendra que les états initial et final soient des états d’équilibre.
Si état initial et état final sont identiques, la transformation est appelée cycle.

Les différents types de transformations

Transformations quasistatiques
Si dans une transformation, le système reste, à chaque instant, très voisin d’un état d ’équilibre, la transformation est dite quasistatique. A chaque instant, en première approximation, les variables d’état restent définies.

Transformations réversibles
Une transformation est dite réversible si le système évolue en passant par une suite continue d’états d’équilibre et s’il existe une transformation permettant de ramener le système et le milieu extérieur, à chaque instant, à l’équilibre précédent. De fait, cette transformation ramène système et milieu extérieur dans leurs états initiaux.
Il y a contradiction entre état d’équilibre et évolution, aussi une transformation réversible n’est pas réalisable en toute rigueur. On peut, au mieux, s’en approcher par une transformation quasistatique avec possibilité de revenir à l’état précédent.

Transformations irréversibles
Ce sont toutes celles qui ne remplissent pas les conditions de la réversibilité.

Remarque
A chaque instant d’une transformation réversible, voire quasistatique, on peut écrire les équations d’état du système. On trouve, en plus, une relation entre les variables d’état liées à la transformation. Il ne faut pas donner un statut d’équation d’état à cette dernière relation.

2. Statique des fluides

2.1. Pression dans un fluide au repos (en équilibre dans un référentiel galiléen)

Notre sens commun nous fait appréhender un fluide (gaz ou liquide) comme étant de nature très différente d’un solide. Ce dernier a une forme propre qui nous permet de le reconnaître. Liquide ou gaz n’ont pas de forme propre, ils épousent la forme du récipient qui les contient, sont déformables sous la moindre action. Liquide et gaz ont des différences : un liquide, contrairement à un gaz, a un volume défini, il ne remplit pas tout le volume du récipient.

2.1.1. Etude expérimentale dans le champ de pesanteur
 

Le tube en U avec la membrane élastique est placé dans l’air atmosphérique : la membrane n’est pas tendue. Nous plaçons l’extrémité avec membrane dans un liquide (ou dans un gaz dont on peut faire varier le volume à l’aide d’un piston) : la membrane élastique est tendue comme indiqué sur la figure ; ceci traduit des efforts du fluide sur la membrane.

La forme de la membrane est indépendante de l’orientation de la membrane autour d’un même point, les efforts sur la membrane sont perpendiculaires à celle-ci.
Si le fluide est un liquide, la déformation de la membrane augmente de manière significative avec la profondeur.

Autre expérience : si, dans un récipient contenant un liquide, nous perçons un trou, l’écoulement de liquide se produit perpendiculairement à l’orifice quelque soit l’orientation de ce dernier.

2.1.2. Définition de la pression dans un fluide
 

Considérons un fluide en équilibre dans un référentiel lié au sol supposé galiléen et une portion de ce fluide limitée extérieurement par un cylindre élémentaire de révolution d’axe AB horizontal et dont les bases sont, en A une section droite dS, en B la surface plane dS’ dont la normale fait un angle a avec l’axe AB. Nous avons .

Cette portion de fluide n’est pas soumise qu’à son seul poids (voire à d’autres forces dues à un champ extérieur) pour être en équilibre. Elle est soumise à des forces " superficielles " (sur les surfaces délimitant le cylindre) dues au fluide extérieure environnant la portion, les forces internes à la portion n’interviennent pas car elles obéissent au principe de l’action et de la réaction.
Les forces exercées par le fluide environnant sur les bases (non matérielles) dS et dS’ du volume élémentaire de fluide sont normales à celles-ci (sinon il y aurait glissement entre les couches du fluide puisqu’un fluide se déforme à la moindre action extérieure).
La condition d’équilibre sur l’axe horizontal se traduit par  .
Soit  qui, par définition, est la pression dans le fluide.

La pression p en un point d’un fluide en équilibre est indépendante de l’orientation de l’élément de surface qui sert à la définir.
La pression est une grandeur scalaire positive, la force de pression est une grandeur vectorielle.
La pression est la même en tous les points d’un plan horizontal pris dans un fluide en équilibre.

2.1.3. Relation locale traduisant l’équilibre d’un fluide dans un référentiel galiléen

Exprimons la relation d’équilibre pour un élément de fluide en forme de parallèpipède rectangle de dimensions dx, dy et dz à partir du point A de coordonnées x, y et z.
Sur la surface rectangulaire ABFE, nous avons une pression  et, sur la surface rectangulaire DCGH, nous avons une pression .
Il en est de même sur les autres faces du parallèpipède rectangle en permutant les coordonnées. Les forces dues à des champs de forces extérieures s’écrivent .
En appliquant les relations d’équilibre de la Mécanique et en projetant suivant la direction Oy, on obtient .

Soit encore 

Sous forme vectorielle, ces trois dernières relations s’écrivent :

Remarque : le gradient de pression n’est due qu’aux champs de forces extérieures.

2.2. Cas d’un fluide au repos dans le champ de pesanteur

Principe de l’hydrostatique (dit de Pascal)

Le fluide a pour masse volumique m et le champ de pesanteur est le seul champ de forces extérieures.
Dans ce cas  relation équivalente à  si l’axe est vertical ascendant. Ceci constitue le principe de l’hydrostatique ou principe de Pascal.

Autre démonstration :
 

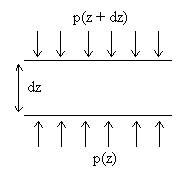Dans le champ de pesanteur, on considère une tranche de fluide à l'altitude z d'épaisseur  en équilibre dans un référentiel lié au sol supposé galiléen. L'axe des z est vertical ascendant, on appelle  la masse volumique du fluide, et les intensités par unité de surface des forces extérieures qui s'exercent sur les bords de la tranche. L'écriture du principe fondamentale de la dynamique conduit à .

L’augmentation de pression entre une altitude z + dz et une altitude z est due au poids du fluide dans le cylindre de hauteur verticale dz et de surface horizontale unitaire.
L’évolution de pression est donc continue, même à la séparation de deux fluides.
La pression a une altitude z est égale au poids, par unité de surface horizontale, des couches de fluide situées à la verticale au-dessus de z.
Dans un même fluide au repos, les surfaces d’égale altitude sont isobares (même pression).
Dans le système MKSA, les pressions se mesurent en N m^-2 que l’on appelle Pascal (Pa).

Attention, il ne faudrait pas conclure que les forces de pression s’exercent verticalement. Elles s’exercent perpendiculairement à tout élément de surface.

2.2.1. Surface de séparation entre deux fluides non miscibles au repos

Considérons deux points de cette surface. Soit dz leur différence d’altitude.
On peut écrire, en négligeant toute discontinuité de la pression à la traversée de la surface de séparation :
ce qui entraîne dz = 0.
La surface de séparation entre deux fluides non miscibles au repos est plane et horizontale.

L’étude de la stabilité de l’équilibre montrerait que le liquide de densité plus faible se place au dessus de celui de densité plus forte.

2.2.2. Fluide incompressible (liquide)

La masse volumique est constante et l’intégration du principe de l’hydrostatique donne 

Applications : baromètre - presse hydraulique

Dans un baromètre à mercure, pour une pression atmosphérique normale, la hauteur h est égale à 760 mm ce qui correspond à .
Souvent, les pressions sont exprimées en mm de mercure, en atmosphère ( 1 atm correspond à la pression atmosphérique normale), en bar (1 bar = 10⁵ Pa) ou millibar (mbar).

Nous remarquerons que pour une hauteur d’eau de 3m, la variation de pression est égale à 30000 Pa soit à peu près le tiers de la pression atmosphérique normale.
A l’échelle humaine courante, les variations de pression sont sensibles dans les liquides.

Un baromètre mesure une pression absolue puisque la pression dans le vide est nulle (pas de masse = pas de poids). Les manomètres qui mesurent les différences de pression seront étudiés en Travaux dirigés et pratiques.

2.2.3. Fluide compressible (gaz)

La masse volumique dépend de la pression et nous le verrons de la température. On ne peut intégrer directement la relation dp = -mg dz.
Cependant les masses volumiques des gaz sont faibles (air dans les conditions courantes 1,3 Kg m^-3) et, à l’échelle humaine courante, on négligera les variations de pression avec l’altitude dans les gaz.
Seul l’air atmosphérique présente des différences d’altitude suffisantes pour ne pas négliger les variations de pression.

2.2.4. Théorème d’Archimède et corps flottants

Théorème d’Archimède

Considérons (Fig. a) un corps entièrement immergé dans un fluide homogène au repos. Il occupe un volume V et subit de la part du fluide des forces de pression.

" Tout corps plongé dans un fluide en équilibre est soumis de la part de celui-ci à une poussée verticale, dirigée de bas en haut, égale au poids du liquide de remplacement et appliquée à son centre de masse appelé centre de carène. "
En effet, en l’absence de corps immergé, le fluide de remplacement serait en équilibre sous l’action des forces de pression exercées par le fluide environnant et des forces de pesanteur. Les forces de pression sont l’opposé du poids du fluide de remplacement.

Autre démonstration : nous appliquons le théorème du gradient (cas particulier du théorème d’Ostrogradsky) pour la résultante des forces de pression sur une surface fermée S contenant le volume V.
(le vecteur  est orienté vers l’extérieur de la surface fermée)
Ce théorème reste vrai si le corps est immergé dans plusieurs fluides en équilibre.

Statique des corps flottants

Lorsque le poids du liquide de remplacement est supérieur au poids du corps, seule une partie de ce dernier est immergée. Le corps est alors soumis à deux forces : son poids, appliqué au centre de masse C, et la poussée d’Archimède appliquée au centre de carène K.

A titre d’exemple, considérons l’équilibre d’une boîte parallélépipédique à section rectangulaire ouverte flottant sur l’eau (Fig. b). Une telle boîte, de dimensions L = 10 m, l = 4 m, h = 3 m et de masse M = 20 t, constitue un modèle simplifié d’une embarcation flottant sur l’eau. Elle s’enfonce dans l’eau d’une hauteur h’ telle que :

Notons que, la boîte étant ouverte et les parois latérales de masse négligeable, le centre de masse C est situé au centre de la base rectangulaire, alors que le centre de carène K est au- dessus de lui à la distance h’/2 . Dans ce cas, l’équilibre est stable : une légère rotation de la boîte autour de l’axe longitudinal passant par le centre de masse produit des oscillations autour de la position d’équilibre.

L’étude de la stabilité de la position d’équilibre, évidemment capitale dans la construction des navires, n’est pas au programme.

2.3. Relation locale traduisant l’équilibre d’un fluide dans un référentiel non galiléen

En Mécanique, on apprend que le mouvement d’une masse " ponctuelle " m (mieux : le mouvement du centre de masse d’un système matériel de masse totale m) est régi, dans un référentiel non galiléen, par la relation  où on introduit les forces d’entraînement et de Coriolis.
L’absence de mouvement relatif imposent accélération et vitesse relatives nulles et donc  et 
Par suite, la relation d’équilibre s’écrit 

Pour le champ de forces extérieures de pesanteur 

2.4. Phénomènes de tension superficielle

Une molécule au sein d’un liquide est soumise de la part des autres molécules à des forces de Van der Waals d’origine électromagnétique qui varient en . Ce type d’interaction décroît très rapidement et peut être négligé au-delà d’une distance de l’ordre d’une dizaine de nanomètres.
A la surface de séparation de deux fluides (liquide-gaz ou liquide-liquide), la situation est différente en particulier l’isotropie des forces qui existe au sein d’un fluide n’est plus la règle et il apparaît un système de forces différent dans la couche capillaire (couche de liquide proche de la surface de séparation de deux fluides et dont l’épaisseur est de l’ordre du nanomètre).
A titre d’exemples, chacun visualisera que l’on peut soulever une pellicule d’eau savonneuse avec un anneau et qu’en soufflant sur cette pellicule on peut former un bulle de savon dont la surface en forme de sphère est tendue.

2.4.1. Tension superficielle
 

				Les phénomènes observés suggère de traiter la couche capillaire comme une membrane élastique supposée d’épaisseur nulle. Effectuons une incision de longueur dl dans la couche capillaire. Les lèvres s’écartent ce qui signifie que préalablement à l’incision, la partie droite D de la couche capillaire exerçait sur l’élément dl appartenant à la partie de gauche G une force attractive  où A, coefficient de tension superficielle s’exprime en .
Liquide	A (N.m-1)	t ( °C )	Remarque : La partie droite D de la couche capillaire peut être remplacée par un solide,la force garde la même valeur
eau		20
éthanol		20
glycérine		20
eau		60

2.4.2. Loi de Laplace

• Pour une goutte sphérique de liquide de rayon R dans l’air, si  est la pression dans le liquide et  celle dans l’air, on montre que 

• Pour une bulle de vapeur de rayon R dans un liquide, si  est la pression dans le liquide et  celle de vapeur, on montre que 

• Pour une bulle de savon de rayon R, si  est la pression dans la bulle et  celle extérieure, on montre que 

Plongeons un tube de faible diamètre (capillaire) dans un liquide contenu dans une cuve de grandes dimensions.Le liquide s’élève dans le tube. Ce phénomène s’appelle capillarité et la loi de Jurin permet d’en rendre compte.A partir de loi de Laplace, on montre la loi de Jurin :

L’angle q de contact dépend de l’interface : il est de 0° pour les interfaces eau-verre propre et éthanol-verre propre et respectivement de 140°, 90° et 107° pour les interfaces mercure-verre, eau-argent et eau-paraffine.

2.4.4. Mesure des tensions superficielles

Il existe plusieurs méthodes de mesure des tensions superficielles. Nous citerons celle utilisant directement la loi de Jurin, celle utilisant l’arrachement d’un solide du liquide et celle utilisant le détachement des gouttes de liquide d’un tube.

3. Température et équation d’état des gaz parfaits

" Il fait chaud ", " il fait froid ", " c’est chaud ", " c’est froid " ... que d’expressions du langage courant pour traduire le fait que la température fait partie du quotidien humain.La première notion de température est physiologique, sensitive.
Cependant, nos sensations sont insuffisantes pour établir une échelle de température et comparer des températures.
L’observation, l’expérience nous apprennent qu’un même système change (par exemple changement de volume) lorsque nos sensations de température évoluent. Ce constat va nous permettre de préciser quantitativement le paramètre physique température.

3.1. Principe de Thermométrie (ou Principe 0 de la Thermodynamique)

Considérons deux corps isolés en état d’équilibre. Mis en contact thermique entre eux (à ce stade de nos connaissances en contact physique) ils évoluent vers de nouveaux états d’équilibre.
Le principe 0 de la Thermodynamique affirme que la variable d’état température est caractéristique des états d’équilibre atteints.
En d’autres termes et en raisonnant de proche en proche, des systèmes mis en contact thermique évoluent vers des états d’équilibre où ils ont même température.

3.2. Echelles de température. Echelle légale

3.2.1. Thermométrie et grandeur thermométrique

La température n’est associée à aucune loi physique, nous pouvons donc choisir des valeurs arbitraires correspondant à des états d’équilibre déterminés. Ainsi la température peut être la valeur d’une grandeur physique (ou une fonction monotone arbitraire de cette grandeur) d’un système à condition d’établir une correspondance bi-univoque entre grandeur physique et température. Par comparaison des états d’équilibre d’autres systèmes avec ceux du système choisi, on mesurera la température des autres systèmes.
Le système choisi est appelé thermomètre, la grandeur physique grandeur thermométrique.

Exemple : le thermomètre est un fil, la grandeur thermométrique sa longueur.
La longueur dépend de la température puisque, si je " chauffe " le fil (je change ma sensation de toucher, je conclus que la température a varié) je constate que la longueur varie.
La température peut être définie soit comme la valeur de la longueur elle-même, soit comme une fonction monotone arbitraire de cette longueur.

Il suit que pour rendre la notion de température quantitativement utilisable par chacun, il a fallu définir une échelle universelle c’est à dire un thermomètre de référence, une grandeur thermométrique et une fonction monotone entre cette grandeur et la température.
La Science ne s’est pas faite en un jour et la définition actuelle de l’échelle légale de température est le résultat de tâtonnements successifs. C’est pourquoi, de nos jours, au quotidien, coexistent l’échelle Kelvin, l’échelle Celsius, l’échelle Farenheit, seule l’échelle Réaumur est tombée en désuétude.

3.2.2. Faits expérimentaux

Points fixes

Certains états d’équilibre sont particulièrement utiles car facilement reproductibles. On les appelle points fixes. Il s’agit des états d’équilibre de deux phases d’un même corps pur sous une pression donnée (solide en fusion, liquide en ébullition, ...) ou de trois phases d’un même corps pur ce qui se produit à une certaine pression (point triple).
Ces états d’équilibre sont facilement reproductibles car indépendants des masses des phases en présence.

Exemple : la résistance ou la longueur d’un fil de platine immergé dans un mélange de glace et d’eau sous une pression donnée est indépendante des masses d’eau et de glace en présence et reprend toujours la même valeur si on refait le mélange, la pression étant inchangée.

Nous savons reproduire facilement des températures.

Le gaz parfait, limite de comportement de tous les gaz réels.

L’expérience montre que, si l’on trace les courbes de compressibilité isotherme pour un nombre donné de molécules, on obtient dans un diagramme p, pV (dit diagramme d’Amagat) les courbes ci-après.

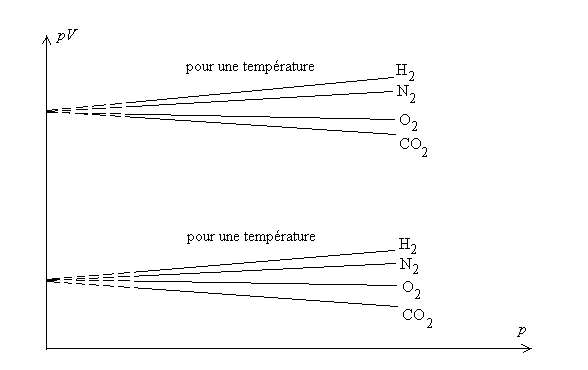
a la même valeur pour une température q fixée. Cette limite est proportionnelle au nombre de molécules N ou de moles n ( N = nN où N = 6,023 10²³ est le nombre d’Avogadro). Cette limite est indépendante du gaz considéré.
Ainsi  pour tous les gaz.

Définition du gaz parfait : Un gaz qui aurait, quelle que soit la pression, le comportement de tout gaz réel à pression nulle est appelée gaz parfait.
Les variables d’état pression p, volume V, température q et nombre de moles n sont liées par l’équation d’état 

3.2.3. Echelle légale de température

Le Kelvin : proposé en 1954, adopté en 1967 par le Comité International des Poids et Mesures, le Kelvin est défini de la manière suivante :

• Le thermomètre de référence est le thermomètre à gaz parfait

• La grandeur thermométrique est le produit pV

• La fonction monotone est linéaire soit pV = nRT

- où le symbole T est réservé à la température Kelvin (appelée aussi absolue)
- où R est la constante des gaz parfaits.

Remarque :  pV = nRT équation liant les variables d'état du gaz parfait est appelée équation d’état des gaz parfaits. Historiquement, cette relation est connue sous le nom de loi de Boyle-Mariotte.
Bien que valable en toute rigueur à la pression nulle, cette équation s’applique avec des précisions très satisfaisantes jusqu’à des pressions de quelques atmosphères pour les gaz réels.
Dans les exercices-type ou mieux dans "l'annexe 1 : Détermination expérimentale des caractéristiques thermodynamiques" le lecteur trouvera des équations d'état pour les gaz réels.

3.2.4. Autres échelles de température

Pour les échelles Celsius (notation t), Farenheit (notation F) et Réaumur (notation R), seule diffère dans la définition la fonction monotone qui reste linéaire mais de la forme pV = aq + b.
Les correspondances sont souvent établies de la manière suivante :

où  correspondent respectivement aux points fixes d’ébullition de l’eau et de fusion de la glace sous la pression atmosphérique normale, les températures respectives étant 373,15 K et 273,15 K soient encore 100 °C et 0 °C.
Il y a une simple translation entre les échelles Celsius et Kelvin (t = T - 273,15).

3.3. La mesure des températures

Mis à part quelques laboratoires spécialement équipés, on ne mesure pas une température avec un " thermomètre à gaz parfait ".
On se sert de thermomètres (et grandeurs thermométriques) que l’on étalonne, dans la gamme de température d’utilisation, à partir des valeurs des températures de points fixes déterminées par ces quelques laboratoires.

3.3.1. Points fixes fondamentaux

On trouvera ci-après les températures officielles assignées à certains points fixes ; ces valeurs, sauf pour les points triples, correspondent à des états d’équilibre sous la pression atmosphérique normale.
 

ETAT D' EQUILIBRE	T	t
Point d'ébullition de l'hélium	4,2	-268,95
Point triple de l'hydrogène	13,81	-259,34
Point d'ébullition de l'hydrogène à 33330,6 Pa	17,04	-256,11
Point d'ébullition de l'hydrogène	20,28	-252,87
Point d'ébullition du néon	27,1	-246,05
Point triple de l'oxygène	54,36	-218,79
Point d'ébullition de l'oxygène	90,19	-182,96
Point de fusion de l'eau	273,15	0
Point triple de l'eau	273,16	0,01
Point d'ébullition de l'eau	373,15	100
Point de fusion du Zinc	692,73	419,58
Point de fusion de l'argent	1235,08	961,93
Point de fusion de l'or	1337,58	1064,43

3.3.2. Les thermomètres

• Le Thermomètre à " gaz parfait "

• Les thermomètres à dilatation de liquide

Les thermomètres à liquide comprennent un réservoir dont le volume n’excède pas 1 cm³ soudé à une tige capillaire de diamètre intérieur de quelques dixièmes de millimètre. La paroi est mince pour permettre l’établissement rapide de l’équilibre thermique.
Avec une bonne approximation, on peut considérer que le volume V du liquide dans le thermomètre varie avec la température suivant la relation 

Pour le mercure dans le verre, on prend pour a la valeur moyenne 1/6300.

Au-dessous de -39 °C, on utilise l’éthanol jusqu’à -80 °C, le toluène jusqu’à -90 °C, le pentane jusqu’à -200 °C.
Au-dessus de 500 °C, le gallium permet d’atteindre 1000 °C.

• Les thermomètres à tension de vapeur saturante

• Les thermocouples

Trois fils constitués de deux métaux ou alliages différents M et M’ sont soudés (ou en contact) en a et b où règnent des températures . Il apparaît en A et B une force électromotrice e fonction de l’écart de températures. Des relations de type  sont utilisées pour déterminer l’écart de température. Leur domaine d’utilisation varie entre -180 et 2500 °C.

• Les thermomètres à résistance

• Les thermistances

• Les thermomètres à quartz

• Les pyromètres optiques

• Les très basses températures (quelques mK)

3.3.3. Thermométrie

Mesurer une température s’avère souvent difficile ; en effet, faire un étalonnage précis d’un thermomètre soulève des problèmes, introduire le thermomètre à l’endroit où l’on veut connaître la température perturbe, parfois notablement, la température.
Nous n’en dirons pas plus dans le cadre de ce cours.

4. Applications simples de l’équation d’état des gaz parfaits

4.1. Un gaz parfait obéit aux lois de Gay-Lussac et de Charles

On dit qu’un gaz obéit à la loi de Gay-Lussac si, à pression constante, son volume est proportionnel à la température.
On dit qu’un gaz obéit à la loi de Charles si, à volume constant, sa pression est proportionnelle à la température.
Pour un gaz parfait à  (Loi de Gay-Lussac)
Pour un gaz parfait à  (Loi de Charles)

4.2. Un gaz qui obéit aux lois de Gay-Lussac et de Charles est un gaz parfait

Loi de Gay-Lussac : à . Si on change la valeur de p, cette dernière constante change. C’est donc une fonction de
Loi de Charles : à . Si on change la valeur de V, cette dernière constante change. C’est donc une fonction de 
En réunissant ces deux résultats, on obtient .
Soit  puisque la relation doit être vraie quels que soient V et p.

soit encore pV = CT

4.3. Mélange idéal de gaz parfaits

Dans une enceinte de volume V, nous mélangeons différentes substances chimiques en phases gazeuses sans possibilité de réactions chimiques entre elles. Le mélange est dit idéal.
Si p la pression du mélange est suffisamment faible, l’expérience montre que :
est le nombre de moles du gaz i et n le nombre total de moles gazeuses sans distinction de la substance gazeuse.
Le mélange se comporte comme un gaz parfait.

Si le gaz i était seul dans l’enceinte, il se comporterait comme un gaz parfait et sa pression  serait donnée par la relation .
On remarquera que la pression p dans le mélange est liée aux pressions  par la relation .
est appelée pression partielle du gaz i dans le mélange. La pression du mélange est la somme des pressions partielles.
On appelle fraction molaire du gaz i dans le mélange, la quantité .
On déduit que .

La quantité  représente la masse totale du mélange si  est la masse molaire du gaz i.

On définit la " masse molaire du mélange " par .

4.4. Autre écriture de l’équation d’état des gaz parfaits

pV = nRT s’écrit aussi pV = (m/M) RT = mrT où r = R/M.
Si N est le nombre de molécules du gaz, N = nN où est le nombre d’Avogadro.
PV = nRT pV = NkT où est la constante de Boltzmann.
L’équation d’état des gaz parfaits s’écrit encore  en introduisant  la densité volumique molaire et  la densité volumique des molécules.
Remarque : localement la pression est proportionnelle à la densité des molécules

4.5. Masse volumique et densité des gaz parfaits

Soit m = m/V la masse volumique. On obtient (autre écriture de l’équation d’état des gaz parfaits).
On appelle densité d’un gaz le rapport de la masse d’un certain volume de gaz sur la masse du même volume d’air pris dans les mêmes conditions de pression et de température.
(en grammes)