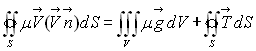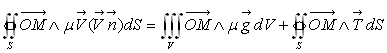Mécanique des fluides
Plan
1. Généralités
1.1. Description du fluide en mouvement
1.2. Dérivation suivant la méthode d'Euler
1.3. Equation de continuité (ou de conservation de la
masse)
1.4. Ecoulement laminaire et turbulent
1.5. Notion de viscosité dans un fluide en mouvement
2. Cinématique des fluides
2.1. Champ de vitesses dans un fluide
2.2. Exemple de compréhension
2.3. Etude des différents types de champ de vitesses
3. Dynamique des fluides
3.1. Equation de Navier. Equation de Navier-Stokes. Equation
d'Euler
3.1.1. Equation de Navier - Stokes pour les fluides parfaits
(équation d'Euler)
3.1.2. Equation de Navier - Stokes pour les fluides incompressibles
3.2. Equation d'Euler et théorème de Bernoulli
3.3. Bilans énergétiques pour les écoulements
permanents
3.4. Théorème d'Euler. Bilan de quantité
de mouvement et de moment cinétique dans un écoulement permanent
1. Généralités
1.1. Description d’un fluide en mouvement
Décrire le mouvement d’un fluide fait appel à
des notions différentes de celles développées en Mécanique
du point ou du solide. Le mouvement d’un fluide est un écoulement
où il y a déformation continue du fluide
On peut, de manière analogue à ce que l’on fait en Mécanique
du solide, isoler (par la pensée ou en trouvant un moyen de visualisation,
coloration par exemple) une partie restreinte du fluide appelée particule
et la " suivre " au cours du temps c’est à dire connaître
à chaque instant sa position.
Cette position sera connue, par exemple, par ses coordonnées cartésiennes
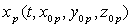 ,
, 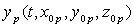 et
et 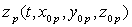 où
où
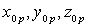 représentent
les coordonnées de la particule choisie à l’instant
représentent
les coordonnées de la particule choisie à l’instant 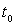 ,
la vitesse de la particule aura pour composantes
,
la vitesse de la particule aura pour composantes 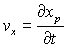 ,
,
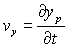 et
et 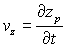 .
Au cours du temps, la particule sera en différents points
.
Au cours du temps, la particule sera en différents points 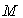 ,
l’ensemble des points
,
l’ensemble des points 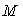 constitue la trajectoire de la particule.
constitue la trajectoire de la particule.
Cette façon de faire est appelée méthode de Lagrange,
les variables introduites sont appelées variables de Lagrange.
La méthode de Lagrange s’avère dans la plupart des cas délicate
car il n’est pas facile de suivre les particules : elle est peu employée.
La méthode d’Euler consiste à connaître
la vitesse des particules au cours du temps 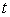 à un endroit donné déterminé par ses coordonnées,
par exemple cartésiennes
à un endroit donné déterminé par ses coordonnées,
par exemple cartésiennes 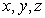 .
Elle est plus employée que la méthode de Lagrange, la connaissance
du champ des vitesses étant suffisante pour la description du fluide
en mouvement.
.
Elle est plus employée que la méthode de Lagrange, la connaissance
du champ des vitesses étant suffisante pour la description du fluide
en mouvement.
Les composantes du vecteur vitesse 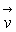 sont des fonctions des variables (
sont des fonctions des variables (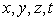 ),
ainsi
),
ainsi 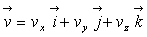 où
où
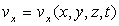 ,
, 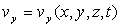 et
et 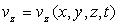
L’écoulement du fluide est permanent ou stationnaire si
ses composantes de vitesse sont indépendantes de la variable temps 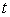 ;
il est dit non-permanent ou instationnaire si cette condition
n’est pas réalisée.
;
il est dit non-permanent ou instationnaire si cette condition
n’est pas réalisée.
L’écoulement du fluide est uniforme si ses composantes de vitesse
sont indépendantes des coordonnées d’espace ; il est non-uniforme
si cette condition n’est pas remplie.
Remarque : Dans la méthode d’Euler, l’accélération
d’une particule peut être due, bien sur, au caractère instationnaire
de l’écoulement mais aussi à sa non-uniformité. Ainsi,
chacun a pu constater, dans l’écoulement permanent d’une rivière,
l’accélération des particules lors du franchissement d’un rétrécissement.
On appelle ligne de courant une courbe dont la direction
tangente en chacun de ses points est la direction du vecteur vitesse. L’équation
d’une ligne de courant se calcule par intégration des équations
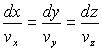 .
.
Un tube de courant est un ensemble de lignes de courant
s’appuyant sur un contour fermé.
On appelle ligne d’émission une courbe constituée par l’ensemble
des points atteints à un instant donné par des particules passées
antérieurement en un même point.
Trajectoire, ligne de courant et ligne d’émission sont confondues pour
un écoulement permanent.
1.2. Dérivation suivant la méthode
d’Euler
Considérons la fonction scalaire 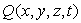 rendant compte d’une grandeur physique caractéristique du fluide au point
de coordonnées
rendant compte d’une grandeur physique caractéristique du fluide au point
de coordonnées 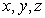 et au temps
et au temps 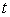 .
.
La particule fluide au temps 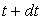 sera au point de coordonnées
sera au point de coordonnées 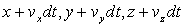 .
.
La variation de la fonction 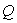 sera donc égale à :
sera donc égale à :
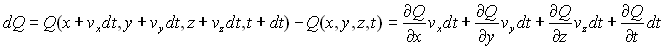
La dérivée 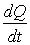 ,
que l’on note
,
que l’on note 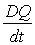 et que l’on appelle dérivée particulaire, est égale
à :
et que l’on appelle dérivée particulaire, est égale
à :
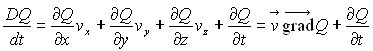
Cette dérivée apparaît comme la somme de
deux termes :
- le premier, qualifié de convectif ou advectif, est
du à la non-uniformité de l’écoulement,
- le second, qualifié de temporel, est du au caractère
instationnaire de l’écoulement.
1.3. Equation de continuité (ou de conservation
de la masse)
La conservation de la masse s’écrit  où
où 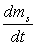 représente
le débit massique de fluide interne au volume considéré,
compté positivement s’il s’agit d’une source et négativement s’il
s’agit d’un puits.
représente
le débit massique de fluide interne au volume considéré,
compté positivement s’il s’agit d’une source et négativement s’il
s’agit d’un puits.
Compte tenu du théorème d’Ostrogradsky 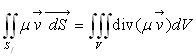 ,
l’équation de conservation de la masse peut être écrite
,
l’équation de conservation de la masse peut être écrite
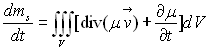
Remarque :
Sauf précision contraire, nous appliquerons l’équation de conservation
de masse en absence de source ou de puits, soit 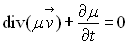 .
.
Deux cas particuliers sont alors à considérer.
Le cas 1 du fluide incompressible (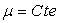 )
ð
)
ð 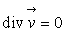 pour un écoulement stationnaire ou instationnaire.
pour un écoulement stationnaire ou instationnaire.
Cet écoulement est dit isovolume.
Le cas 2 d’un écoulement stationnaire
(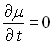 ) ð
) ð
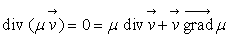
En dehors de la possibilité cas 1, il existe la possibilité
d’écoulements isovolumes tels que 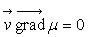 où les variations de masse volumique sont orthogonales, en tout point,
au vecteur vitesse.
où les variations de masse volumique sont orthogonales, en tout point,
au vecteur vitesse.
Ce cas correspond à des écoulements stratifiés par
salinité ou température (courants marins), par température
et humidité (atmosphère).
1.4. Ecoulements laminaire et turbulent
L’introduction de marqueurs (fumée dans le cas
des gaz, colorant pour les liquides), permet d’observer des différences
importantes dans le comportement des écoulements des fluides.
Dans certains écoulements, les particules marquées diffusent très
lentement c’est à dire s’écartent peu les unes des autres, les
différentes couches (lamelles) glissent les unes par rapport les autres
sans se mélanger : l’écoulement est dit laminaire.
Au contraire dans d’autres écoulements les particules marquées
s’éloignent très rapidement de manière " aléatoire,
irrégulière, dans toutes les directions " les unes des
autres, on ne retrouve plus de trace de marquage significative très près
de l’endroit où le marqueur a été introduit : l’écoulement
est dit turbulent.
D’évidence, l’écoulement sera laminaire à faible vitesse
alors que les grandes vitesses provoqueront l’instabilité des particules
c’est à dire le caractère turbulent de l’écoulement. En
fait, la transition entre écoulement laminaire et turbulent dépend
de la vitesse, mais aussi des caractéristiques (viscosité) du
fluide, de la forme de l’écoulement (espace fermé –canalisation- ;
espace ouvert –sur une surface à " l’air libre "-).
Il découle de ces propos que, pour un écoulement turbulent, les
variables, en un point donné, qui caractérisent l’écoulement
varient de manière aléatoire et que la notion d’écoulement
permanent ne peut être comprise qu’en moyenne (la valeur moyenne de toute
variable caractéristique de l’écoulement étant, alors,
indépendante du temps).
Au contraire, pour un écoulement laminaire, les fluctuations des variables
sont négligeables, à la limite nulles.
1.5. Notion de viscosité dans un fluide
en mouvement
L’expérience montre que, lors d’un écoulement
d’un fluide, la pression (force normale) ne suffit pas à expliquer les
phénomènes et qu’il convient d’introduire des forces tangentielles
qui s’opposent au mouvement du fluide. Ces forces, de type frottement, dues
aux interactions entre molécules du fluide, sont appelées forces
de viscosité.
|
|
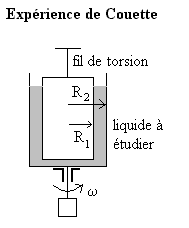
On constate que lorsque le cavité cylindrique
extérieure est mis en rotation à vitesse 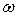 ,
le cylindre intérieur tourne d’un angle ,
le cylindre intérieur tourne d’un angle 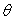 par rapport à sa position d’équilibre. Le fil de torsion
exerce un couple de rappel
par rapport à sa position d’équilibre. Le fil de torsion
exerce un couple de rappel 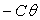 qui équilibre des efforts tangentiels au cylindre. La notion de
pression ne suffit pas pour rendre compte du système de forces.
qui équilibre des efforts tangentiels au cylindre. La notion de
pression ne suffit pas pour rendre compte du système de forces.
Pour les liquides purs de faible masse molaire ou les
solutions peu concentrées, le couple est proportionnel à
la vitesse de rotation et inversement proportionnel à l’épaisseur
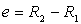 si si 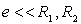 . .
|
|
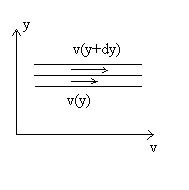
|
Entre deux couches successives de fluides à vitesses
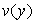 et et 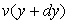 ,
on introduit des forces parallèles à l'écoulement
qui accélèrent la couche la plus lente et ralentissent la
couche la plus rapide. ,
on introduit des forces parallèles à l'écoulement
qui accélèrent la couche la plus lente et ralentissent la
couche la plus rapide.
On appelle fluides newtoniens, les fluides pour
lesquelles ces forces obéissent à la loi générale :
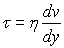
|
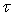 (force par unité de surface dans le plan tangent à deux couches
successives) est appelée contrainte tangentielle et
(force par unité de surface dans le plan tangent à deux couches
successives) est appelée contrainte tangentielle et 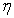 viscosité dynamique qui, dans le système MKSA s’exprime
viscosité dynamique qui, dans le système MKSA s’exprime 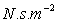 ou
ou 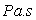 ( appelé
poiseuille).
( appelé
poiseuille).
Si nous supposons 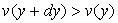 ,
la couche de fluide située en
,
la couche de fluide située en 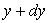 " tire " sur la couche de fluide en
" tire " sur la couche de fluide en 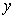 avec la contrainte
avec la contrainte 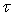 .
Evidemment, la couche en
.
Evidemment, la couche en 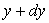 est retenue par une contrainte
est retenue par une contrainte 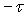 .
.
Dans l’expérience Couette la contrainte est égale à :
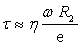 .
.
On trouvera, dans le tableau ci-après, quelques valeurs
de la viscosité à 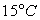 .
.
|
Ether
|
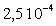
|
Mercure
|
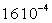
|
|
Chloroforme
|
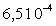
|
Kérosène
|
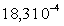
|
|
Benzène
|
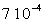
|
Glycérine
|
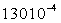
|
|
Eau
|
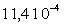
|
Huile de ricin
|
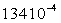
|
|
Alcool
|
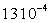
|
|
|
Pour tous les liquides, la viscosité diminue lorsque
la température augmente.
Pour des liquides purs, on utilise la loi empirique 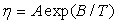 ,
pour des mélanges
,
pour des mélanges 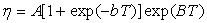 .
.
Dans le cas des huiles multigrades, les coefficients  sont tels que
sont tels que 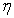 est à peu près la même valeur à basse et haute températures.
est à peu près la même valeur à basse et haute températures.
Pour les gaz, la viscosité est beaucoup plus faible et varie avec la
température suivant la loi 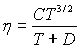 .
.
Dans le cas de fluides non-newtoniens, il n’y a pas proportionnalité
entre la contrainte tangentielle et le gradient de vitesse. C'est le cas des
solutions de polymères, des purées de légumes, des gels,
des boues, des pâtes, du sang, des peintures, ..L'étude de ces
fluides relève de la rhéologie.
Un fluide est dit non-visqueux (ou parfait) si
l’on peut négliger les contraintes tangentielles.
2. Cinématique des fluides
2.1. Champ de vitesses d’un fluide
Au cours du mouvement, une particule de fluide subit des changements
de position, d’orientation et de forme. Nous considérons deux points
voisins d’un même fluide 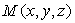 et
et 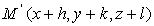 et leurs
vitesses respectives soient
et leurs
vitesses respectives soient  à un instant
à un instant 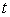 .
.
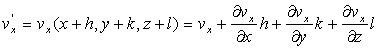
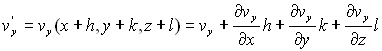
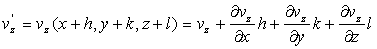
Ces expressions peuvent être écrites,
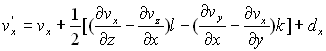 où
où 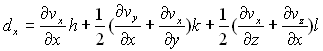
 où
où 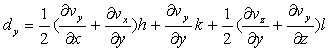
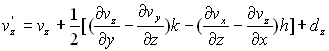 où
où 
soit 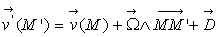 où
où 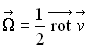 est
le vecteur tourbillon et
est
le vecteur tourbillon et 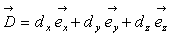 est la vitesse de déformation.
est la vitesse de déformation.
|
|
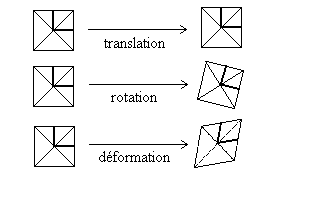
D’une manière générale, le mouvement
d’une particule fluide est la superposition d’une translation, d’une rotation
et d’une déformation.
|
Ces résultats peuvent être présentés
sous forme tensorielle. On introduit alors le tenseur rotation et le tenseur
déformation.
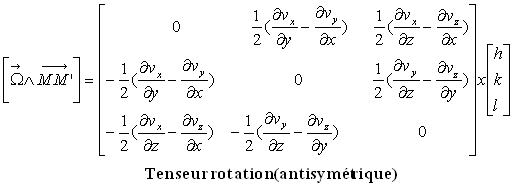
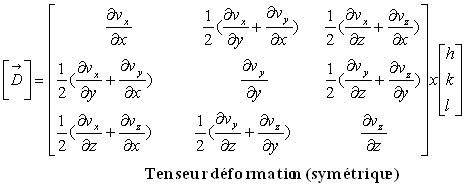
2.2. Exemples de compréhension
La notion de translation ne pose pas de difficulté :
il suffit de se représenter l’écoulement d’une rivière
" paisible ".
Les notions de rotation (appréhendée en Mécanique du solide)
et de déformation méritent attention.
Certains écoulements présentent des lignes de courant fermées
" circulaires en première approximation " de type
" tourbillonnaire ".
Nous pensons aux tourbillons qui se forment dans le sillage d’un objet solide
en mouvement relatif par rapport à un fluide, à la vidange d’un
réservoir (baignoire, lavabo) par un siphon, aux tornades ou cyclones.
En s’écartant du centre du tourbillon, la vitesse radiale des particules
peut être croissante ou décroissante. Souvent la vitesse est croissante
près du centre puis décroissante.
Nous envisageons les deux cas.
a) L’intensité de vitesse est croissante de type 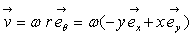
Le calcul montre que : 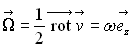 et
et 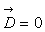
La particule fluide est en rotation
pure et ne se déforme pas (le mouvement est analogue à celui d’un
solide en rotation).
b) L’intensité de vitesse est décroissante
de type 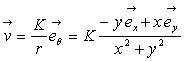
Le calcul montre que : 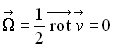 et
et 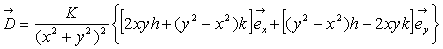
La particule fluide n’a pas de rotation, son mouvement provoque
sa déformation angulaire.
2.3. Etude des différents types de champ
de vitesses
2.3.1. Notion de circulation
|
|
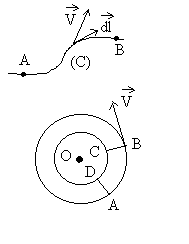
Par définition, la circulation du vecteur vitesse
suivant une courbe est égale à 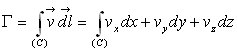
Pour une courbe fermée,
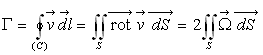 où où
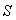 est une
surface quelconque s’appuyant sur le contour est une
surface quelconque s’appuyant sur le contour 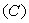 [Stokes].
[Stokes].
|
A titre d’exemple, nous reprenons les deux cas étudiés
en 2.2.
a) 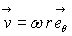
La circulation suivant un cercle de rayon 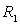 est égale à
est égale à 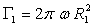 ,
elle dépend du cercle choisi, plus généralement de la courbe
fermée entourant le point O.
,
elle dépend du cercle choisi, plus généralement de la courbe
fermée entourant le point O.
La circulation suivant le contour ABCD d’ouverture d’angle 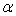 est égale à
est égale à 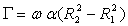 .
Cette valeur est non nulle et nous avions trouvé un vecteur tourbillon
non nul (
.
Cette valeur est non nulle et nous avions trouvé un vecteur tourbillon
non nul (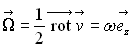 )
)
b) Reprenons le même exemple avec une intensité de vitesse
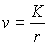 .
.
La circulation suivant un cercle de rayon 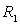 est égale à
est égale à  ,
elle est la même quelque soit le cercle ou la courbe fermée entourant
le point
,
elle est la même quelque soit le cercle ou la courbe fermée entourant
le point 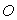 .
.
La circulation suivant le contour ABCD d’ouverture d’angle 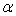 est nulle, elle est nulle quelque soit la courbe fermée n’entourant pas
le point
est nulle, elle est nulle quelque soit la courbe fermée n’entourant pas
le point 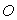 .
.
Cette valeur est nulle et nous avions trouvé un vecteur tourbillon nul.
2.3.2. Ecoulements irrotationnels ou à potentiel des
vitesses
L’écoulement est irrotationnel si 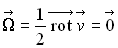
Cette propriété a pour conséquence 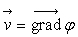 :
le vecteur vitesse
:
le vecteur vitesse 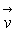 dérive d’une fonction potentiel
dérive d’une fonction potentiel 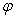 .
L’écoulement est dit à potentiel des vitesses ou plus simplement
écoulement potentiel.
.
L’écoulement est dit à potentiel des vitesses ou plus simplement
écoulement potentiel.
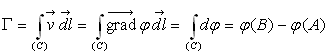 La circulation
du vecteur vitesse est indépendante du chemin suivi pour un écoulement
potentiel.
La circulation
du vecteur vitesse est indépendante du chemin suivi pour un écoulement
potentiel.
En introduisant l’équation de conservation de la masse on obtient 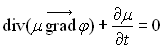 .
.
Dans le cas d’un fluide incompressible (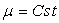 ),
on obtient
),
on obtient 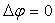
2.3.3. Ecoulements rotationnels : théorie tourbillonnaire
Dans ce type d’écoulements, 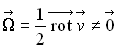
Pour une courbe fermée, 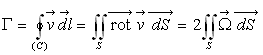 où
où 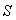 est une surface quelconque
s’appuyant sur le contour
est une surface quelconque
s’appuyant sur le contour 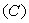 [Théorème de Stokes].
[Théorème de Stokes].
La quantité 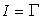 est appelée intensité du tourbillon.
est appelée intensité du tourbillon.
On appelle ligne tourbillon, une ligne tangente en chaque point au vecteur
tourbillon 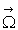 en ce
point et filet tourbillon, l’ensemble des lignes tourbillon s’appuyant
sur une courbe fermée infiniment petite.
en ce
point et filet tourbillon, l’ensemble des lignes tourbillon s’appuyant
sur une courbe fermée infiniment petite.
Le vortex est le cas particulier d’un filet tourbillon unique d’intensité
finie.
Le cas particulier du vortex rectiligne est particulièrement important :
il correspond à un champ de vitesses contenu dans le plan perpendiculaire
au filet tourbillon, de direction radiale et d’intensité de vitesse 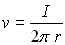 où
où 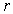 représente
la distance entre le point considéré et le filet tourbillon.
représente
la distance entre le point considéré et le filet tourbillon.
2.3.4. Ecoulement potentiel avec circulation
Dans de nombreux cas, l’écoulement est irrotationnel
dans tout l’espace sauf en un certain nombre de points singuliers pour lesquels
le vecteur tourbillon est différent de zéro. Ces points se groupent
suivant un certain nombre de filets tourbillons distincts.
De tels écoulements sont dits : écoulements à potentiel
des vitesses avec circulation.
Ils possèdent la propriété d’avoir une circulation du vecteur
vitesse nulle suivant toute courbe fermée n’entourant pas un filet tourbillon,
la circulation est constante et différente de zéro lorsque la
courbe entoure (une fois) le filet tourbillon. Cette valeur est égale
à l’intensité du filet tourbillon.
2.3.5. Ecoulement isovolume
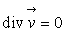 ð
ð
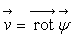 : : le
vecteur vitesse
: : le
vecteur vitesse 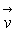 dérive d’un potentiel vecteur
dérive d’un potentiel vecteur 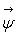 .
.
Nous avons vu que ce type d’écoulement correspond au
cas général de l’écoulement des fluides incompressibles
et aussi d’écoulements stratifiés.
Pour un écoulement plan xOy, on a : 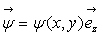 ;
;
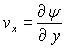 ;
; 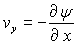
Les lignes de courant sont définies par : 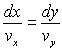 ð
ð 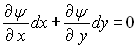 ð
ð 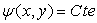
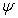 est appelé fonction courant.
est appelé fonction courant.
Le débit entre les deux lignes de courant est indépendant
du chemin pris pour aller d’une ligne à l’autre.
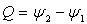
2.3.6. Ecoulement isovolume et rotationnel
Pour ce type d'écoulement : 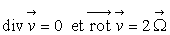
On remarque que ces équations sont analogues à celles de la magnétostatique
 et donnent lieu
aux mêmes traitements mathématiques.
et donnent lieu
aux mêmes traitements mathématiques.
Il existe donc l’équivalent de la loi de Biot-Savart : 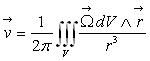
Structure tourbillonnaire
Cette structure correspond à une situation bidimensionnelle où
le fluide tourne autour de l’axe des z avec une vitesse orthoradiale 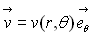 .
.
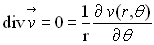 ð
ð
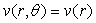
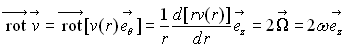
Une telle structure du champ de vitesse correspond à 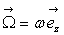 :
ce résultat était évident par analogie au champ magnétique
créé par un courant électrique à section circulaire
de longueur infinie.
:
ce résultat était évident par analogie au champ magnétique
créé par un courant électrique à section circulaire
de longueur infinie.
Nous traitons le cas idéalisé où 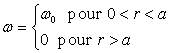
Pour 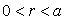 ,
, 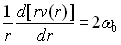 ð
ð 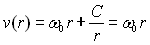 car
car 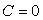 sinon
sinon 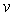 deviendrait infini en
deviendrait infini en  .
.
Pour 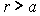 ,
, 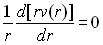 ð
ð 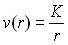
La
continuité de la vitesse en 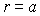 permet d’obtenir
permet d’obtenir 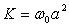
Remarques :
- ces résultats auraient pu être obtenus à partir de
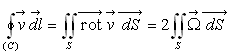 (analogue du
théorème d’Ampère en Magnétostatique),
(analogue du
théorème d’Ampère en Magnétostatique),
- pour 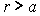 ,
,
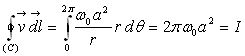 (intensité
du tourbillon).
(intensité
du tourbillon).
2.3.7. Ecoulement isovolume et irrotationnel
Pour ce type d'écoulement : 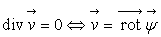 et
et 
On obtient,
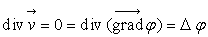
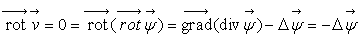 en introduisant
une relation de jauge
en introduisant
une relation de jauge 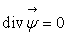 .
.
Pour un écoulement plan xOy, on a
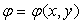 ;
; 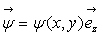 ;
;
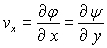 ;
; 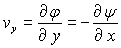
La
condition 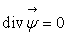 est
naturellement satisfaite, c’est à dire que la solution
est
naturellement satisfaite, c’est à dire que la solution 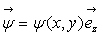 est unique.
est unique.
Dans ce type d’écoulement on introduit la fonction
potentiel complexe,
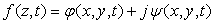 où
où 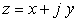
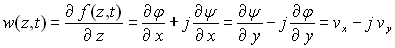
3. Dynamique des fluides
3.1. Equation de Navier. Equation de Navier-Stokes.
Equation d'Euler
Il s’agit d’écrire l’équation fondamentale de
la dynamique pour la particule fluide de masse 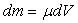 ,
soit dans un référentiel galiléen
,
soit dans un référentiel galiléen 
Les forces extérieures sont de trois types,
- celles dues à un ou plusieurs champ(s) de forces extérieures
(le cas courant étant le champ de pesanteur
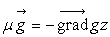 )
)
- celles dues aux forces de pression mécanique
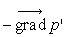
- celles de viscosité
Analyse simplifiée
L’accélération se calcule à partir de
la formule de dérivation explicitée dans la paragraphe 1.2.
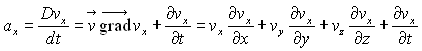 ð
ð

Nous écrivons le principe fondamental de la dynamique
pour un élément de fluide compris entre 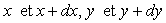 ,
de profondeur (direction
,
de profondeur (direction 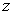 ) unitaire.
) unitaire.
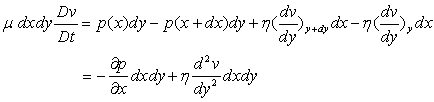
Soit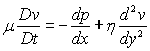
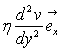 apparaît comme la densité volumique des forces de viscosité.
apparaît comme la densité volumique des forces de viscosité.
Pour un écoulement quelconque, la généralisation de cette
formule conduit à 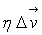 (densité volumique des forces de viscosité) et à l’équation,
(densité volumique des forces de viscosité) et à l’équation,
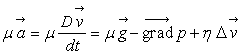
Analyse approfondie
L’analyse des forces de viscosité et l’hypothèse,
pour un fluide newtonien, de proportionnalité entre forces de viscosité
par unité de surface (contraintes) et déformations de la particule
fluide conduisent au tenseur des contraintes visqueuses et aux formules de Lamé
ci-après.
 le tenseur des contraintes visqueuses est un tenseur symétrique
le tenseur des contraintes visqueuses est un tenseur symétrique
Les valeurs des composantes (contraintes visqueuses) sont données
par les formules de Lamé :
 ;
; 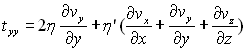 ;
;

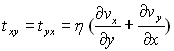 ;
; 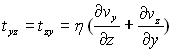 ;
;
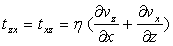
En plus de la
viscosité 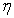 (dite viscosité de cisaillement), on introduit la viscosité de
dilatation
(dite viscosité de cisaillement), on introduit la viscosité de
dilatation 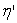 .
.
L’accélération se calcule à partir de
la formule de dérivation explicitée dans la paragraphe 1.2.
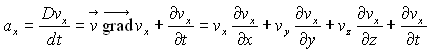
En introduisant des relations identiques suivant les deux autres
directions d’espace, on obtient :
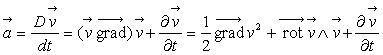 où
où 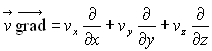 est un opérateur.
est un opérateur.
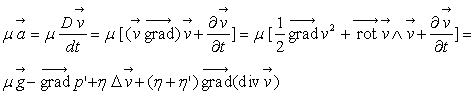 est l’équation de la dynamique des fluides dite de Navier pour
un fluide newtonien dans le seul champ de forces extérieures de pesanteur.
est l’équation de la dynamique des fluides dite de Navier pour
un fluide newtonien dans le seul champ de forces extérieures de pesanteur.
La quantité 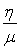 est appelée viscosité cinématique de cisaillement.
est appelée viscosité cinématique de cisaillement.
Remarques sur la complexité de l’équation
de Navier
- les viscosités dépendent de l’écoulement et l’écoulement
dépend des viscosités (en particulier, pour traduire la
nature turbulente d’un écoulement, on doit introduire des termes, dits
de viscosité turbulente, supplémentaires liées aux fluctuations),
- on montre, à partir du second principe de la Thermodynamique, que
la quantité
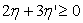 ,
,
- on montre que la pression mécanique
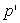 se confond avec la pression thermodynamique
se confond avec la pression thermodynamique 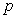 si l’écoulement est isovolume (
si l’écoulement est isovolume (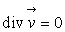 )
ou si la condition de Stokes (
)
ou si la condition de Stokes (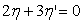 ),
qui fait l’hypothèse de réversibilité des déformations,
est satisfaite,
),
qui fait l’hypothèse de réversibilité des déformations,
est satisfaite,
- si la condition de Stokes est satisfaite, l’équation de Navier
devient l’équation de Navier-Stokes :
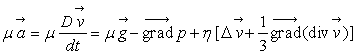 .
.
Les applications de ce cours sont limitées :
- à l’approximation des fluides non-visqueux (parfaits),
- et aux fluides réels incompressibles.
3.1.1. Equation de Navier-Stokes pour les fluides
non-visqueux (parfaits)
Dans ce cas particulier, l’équation de Navier-Stokes
est appelée équation d’Euler.
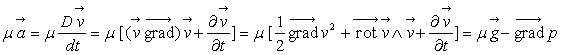
Ecriture de l’équation d’Euler dans le repère
de Frénet
|
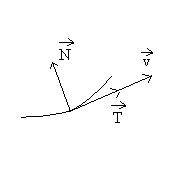
|
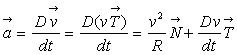 où
où 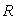 est le rayon de
courbure. est le rayon de
courbure.
Si 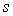 est l’abscisse curviligne,
est l’abscisse curviligne,

ð 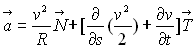
|
L’équation d’Euler s’écrit 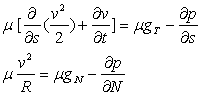
Approximation "fluide non-visqueux (parfait)"
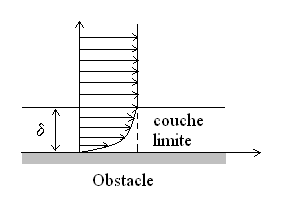
Le fluide non-visqueux n'existe pas et il s'établit
au proche voisinage d'un objet solide une couche limite dans le fluide en écoulement.
|
|
Dans la couche limite la vitesse varie rapidement en
s'éloignant de l'obstacle, alors qu'en dehors de la couche limite
la vitesse est uniforme dans une section droite.
En dehors de la couche limite, le champ des vitesses obéit à
l'équation d'Euler, le fluide se comporte comme un fluide parfait.
Dans la couche limite, on ne peut négliger les forces de viscosité,
en particulier au contact de l'obstacle où vitesse du fluide et
vitesse du point en contact de l'obstacle sont identiques même pour
des viscosités faibles.
|
Pour un obstacle immobile dans le référentiel
d'étude, les vitesses des particules fluide au contact sont nulles …
ce qui n'est pas le cas dans l'approximation fluide parfait.
L'étude des écoulements de fluides visqueux montre
que l'introduction du nombre (sans dimension) de Reynolds est fondamental :
- pour déterminer la nature de l'écoulement (laminaire pour
Re < 2000 ; turbulent pour Re > 6000 ; de transition pour
2000 < Re < 6000),
- pour connaître l'importance des forces de frottement (le coefficient
de frottement Cx dépendant de Re)
- ou pour évaluer l'épaisseur d
de la couche limite qui diminue lorsque Re augmente.
Le nombre de Reynolds est défini par 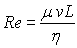 où v est la vitesse du fluide "loin" de l'obstacle et L
une dimension caractéristique de l'obstacle (la longueur dans le sens
de l'écoulement dans le cas d'une plaque, le diamètre pour une
conduite circulaire, …)
où v est la vitesse du fluide "loin" de l'obstacle et L
une dimension caractéristique de l'obstacle (la longueur dans le sens
de l'écoulement dans le cas d'une plaque, le diamètre pour une
conduite circulaire, …)
3.1.2. Equation de Navier-Stokes pour les fluides réels incompressibles
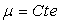 ð
ð 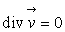 ,
l’équation de Navier devient :
,
l’équation de Navier devient :
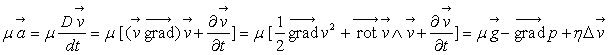
Fluides compressibles ou fluides incompressibles
Un fluide est dit incompressible lorsque sa masse volumique
ne dépend pas (pratiquement pas) de la pression ou de la température.
Généralement, en Statique des fluides, les liquides sont considérés
comme incompressibles et les gaz sont compressibles.
Pour un fluide en écoulement, ce classement est infirmé
dans un certain nombre de situations importantes :
- pour les gaz et pour les liquides, des gradients de température décroissant
avec l'altitude provoquent des mouvements ascensionnels de matière
(convection naturelle) qui ont pour conséquence d’homogénéiser
la température ; ces mouvements ne peuvent s'expliquer sans considérer
des variations de masse volumique,
- dans les gaz et les liquides, des perturbations de pression donnent naissance
à des phénomènes de propagation (onde sonore) qui ne
peuvent être expliqués sans la notion de compressibilité,
- l’approximation fluide incompressible est souvent justifiée pour
un gaz s’écoulant, dans un plan horizontal, jusqu'à des vitesses
égales au tiers de la vitesse du son égale à 340 m/s
pour l'air dans les conditions courantes.
Ainsi c’est la nature de l’écoulement qui permet de
distinguer l’écoulement compressible de l’écoulement incompressible
et non la nature du fluide.
On emploie l’expression hydrodynamique pour qualifier un écoulement
incompressible sans qu’il soit nécessaire que le fluide soit de l’eau
ou un liquide et l’expression aérodynamique pour qualifier l’écoulement
d’un fluide compressible sans qu’il soit nécessaire que ce fluide soit
de l’air ou un gaz.
3.2. Equation d’Euler et théorème de Bernoulli
Multiplions scalairement l’équation d’Euler par le déplacement
élémentaire 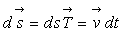 suivant une ligne de courant. En remarquant que la quantité
suivant une ligne de courant. En remarquant que la quantité 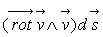 est nulle puisque le produit mixte comporte deux vecteurs parallèles,
on obtient :
est nulle puisque le produit mixte comporte deux vecteurs parallèles,
on obtient :
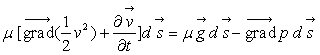 ð
ð
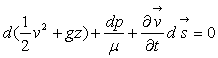
Un fluide (surtout les gaz) est peu conducteur de la chaleur si bien que l’hypothèse
" transferts d’énergie thermique négligeables "
est raisonnable (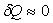 ).
).
La quantité 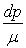 est, dans ce cas, égale à
est, dans ce cas, égale à 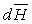 si bien qu’en intégrant suivant une ligne de courant, on obtient
si bien qu’en intégrant suivant une ligne de courant, on obtient 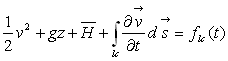 où la " constante " d’intégration
où la " constante " d’intégration 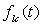 dépend
de la ligne de courant considérée.
dépend
de la ligne de courant considérée.
3.2.1. Cas d’un écoulement permanent
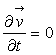 ð
ð 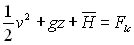 où
où 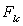 est
une constante dépendant de la ligne de courant considérée.
est
une constante dépendant de la ligne de courant considérée.
3.2.2.Cas d’un écoulement irrotationnel
La quantité 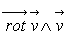 est nulle, il n’est plus nécessaire de se placer suivant une ligne de
courant.
est nulle, il n’est plus nécessaire de se placer suivant une ligne de
courant.
On obtient 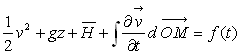 où la " constante " d’intégration
où la " constante " d’intégration 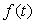 est indépendante de la ligne de courant et a même valeur dans tout
le fluide.
est indépendante de la ligne de courant et a même valeur dans tout
le fluide.
Pour un fluide incompressible (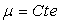 ),
il est intéressant d’introduire la relation
),
il est intéressant d’introduire la relation 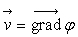 ,
le théorème de Bernoulli s’écrit alors :
,
le théorème de Bernoulli s’écrit alors :  .
.
3.2.3. Cas d’un écoulement permanent irrotationnel
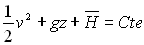
3.2.4. Rappel de Thermodynamique. Ecritures pour un fluide incompressible et pour un fluide compressible de type gaz parfait.
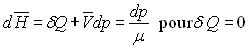
a)
Pour un fluide incompressible, 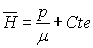 .
.
L’équation 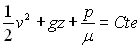 ,
obtenue pour l’écoulement permanent, irrotationnel d’un fluide incompressible
porte plus particulièrement le nom d’équation de Bernoulli.
,
obtenue pour l’écoulement permanent, irrotationnel d’un fluide incompressible
porte plus particulièrement le nom d’équation de Bernoulli.
b) Pour un fluide compressible de type gaz
parfait, 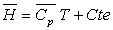
L’équation 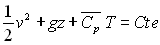 ,
obtenue pour l’écoulement permanent, irrotationnel d’un fluide compressible
type gaz parfait porte le nom de Saint Venant.
,
obtenue pour l’écoulement permanent, irrotationnel d’un fluide compressible
type gaz parfait porte le nom de Saint Venant.
Pour la résolution, l’équation de Saint Venant est à compléter
par l’équation d’état des gaz parfaits 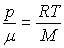 et par l’équation d’isentropicité
et par l’équation d’isentropicité 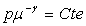 .
.
3.3. Bilans énergétiques pour
des écoulements permanents
3.3.1. Bilan énergétique
Cette masse 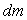 est, à l’instant
est, à l’instant 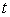 ,
à pression
,
à pression 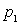 ,
à vitesse
,
à vitesse  et à l’altitude
et à l’altitude  ;
elle est, à l’instant
;
elle est, à l’instant 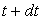 ,
à pression
,
à pression 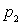 ,
à vitesse
,
à vitesse 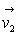 et à l’altitude
et à l’altitude 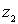 .
.
Le bilan énergétique (application du premier principe de la Thermodynamique
pour un système ouvert) conduit à :
 où
où 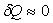 (hypothèse " transferts d’énergie thermique négligeables ").
(hypothèse " transferts d’énergie thermique négligeables ").
Si on néglige le phénomène de viscosité (
ð pas de perte d’énergie mécanique
par frottement entre deux tubes de courant adjacents), le travail  se
confond avec le travail de transvasement, soit
se
confond avec le travail de transvasement, soit 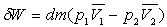 .
.
En reportant cette dernière expression, on retrouve, par bilan énergétique,
l’équation 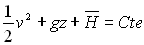 .
.
Remarques :
- l’établissement de l’équation de bilan énergétique
a été faite pour un filet de fluide où on peut considérer
que pression, vitesse et énergie potentielle sont uniformes sut toute
section droite du filet ; on notera que, pour la surface plane d’un liquide
au contact avec un gaz, ces conditions sont remplies, cette surface n’étant
pas de dimensions faibles
- dans le cas des écoulements irrotationnels, on montre (voir paragraphe
précédent) que la valeur de la constante est indépendante
du tube de courant.
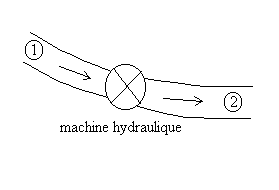
3.3.2. Présence d’une machine hydraulique dans l’écoulement
|
|
Il faut tenir compte de l’énergie mécanique
fournie (pompe) ou absorbée (turbine) par la machine.
Pour un écoulement de fluide non visqueux :
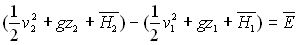
où
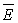 est l’énergie
massique de la machine. Elle est positive pour une pompe, négative
pour une turbine. est l’énergie
massique de la machine. Elle est positive pour une pompe, négative
pour une turbine. |
La puissance de la pompe ou de la turbine est 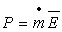 si
si 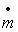 est le débit
massique.
est le débit
massique.
3.3.3. Pertes de charges
Perte de charge " linéaire "
ou " linéique "
L’écoulement permanent de fluides visqueux dans une
conduite droite, horizontale, à section constante, fait apparaître
des chutes de pression liées à la longueur de la conduite et à
la viscosité.
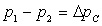 (perte de charge
linéaire)
(perte de charge
linéaire)
Plus généralement, il convient d’écrire le théorème
de Bernoulli sous la forme :
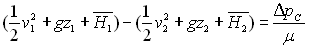
Sous forme adimensionnelle, on introduit le coefficient de
perte de charge 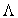 par la relation :
par la relation :
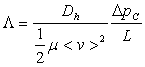 où
où
-  est la longueur
de la conduite,
est la longueur
de la conduite,
- 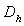 le diamètre
hydraulique de la conduite définie par
le diamètre
hydraulique de la conduite définie par 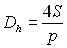 (
(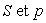 étant
respectivement la section et le périmètre de la conduite),
étant
respectivement la section et le périmètre de la conduite),
- 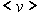 la vitesse
moyenne de débit définie par
la vitesse
moyenne de débit définie par 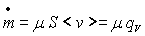 où
où  est
le débit volumique.
est
le débit volumique.
Loi de Poiseuille : pour un écoulement laminaire dans une
conduite circulaire de rayon R, on démontre que 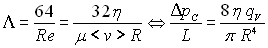 .
Le résultat présenté sous la deuxième forme, est
appelé Loi de Poiseuille.
.
Le résultat présenté sous la deuxième forme, est
appelé Loi de Poiseuille.
Perte de charge singulière
Il existe, aussi, des pertes de charges dites singulières
lors de modifications de la géométrie de la conduite (élargissement
ou contraction brusque de la veine, coude, passage à travers une grille,
vanne, robinet, …).
Contrairement au cas des pertes de charges linéaires où le calcul
théorique est possible dans quelques cas simples, on a recours, pour
les pertes de charges singulières à des données semi-empiriques.
3.4. Théorème d’Euler. Bilan
de quantité de mouvement et de moment cinétique dans un écoulement
permanent
Bilan de quantité de mouvement
Nous reprenons le schéma du tube de courant.
La masse M+dm à l’instant t a une quantité
de mouvement : 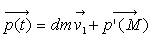
La masse M+dm à l’instant t+dt a une quantité
de mouvement : 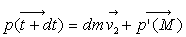
Ainsi 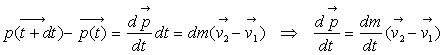
Le principe fondamental de la dynamique permet d’écrire
le théorème d’Euler :
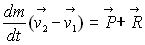 où
où 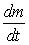 est
le débit massique du fluide,
est
le débit massique du fluide, 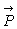 est le poids de fluide considéré (si on se limite à des
forces de volume de pesanteur) et
est le poids de fluide considéré (si on se limite à des
forces de volume de pesanteur) et 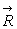 l’action sur la portion de fluide considérée des éléments
en contact avec celle-ci (forces de pression si on ne considère pas les
efforts de viscosité).
l’action sur la portion de fluide considérée des éléments
en contact avec celle-ci (forces de pression si on ne considère pas les
efforts de viscosité).
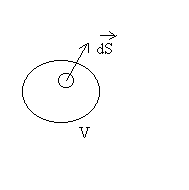
Pour un volume de contrôle quelconque où S est la surface
fermée le délimitant, le débit massique sortant par un
élément 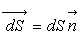 est égal à
est égal à 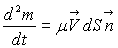 .
.
Pour ce débit massique, le " débit " de quantité
de mouvement est égal à  .
.
En intégrant au volume de contrôle, on obtient le théorème
d’Euler :
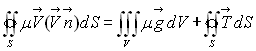
En utilisant
le principe de l’action et de la réaction, on accède simplement
à l’action du fluide sur les parois en contact.
Bilan de moment cinétique
Un raisonnement de même type conduit au bilan de moment
cinétique : 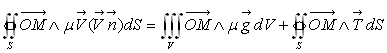
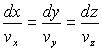 .
.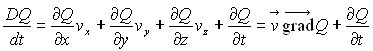
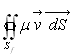 .
.
 où
où 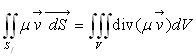 ,
l’équation de conservation de la masse peut être écrite
,
l’équation de conservation de la masse peut être écrite
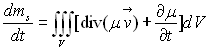

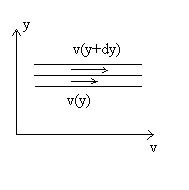
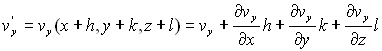
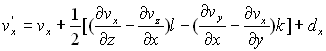 où
où 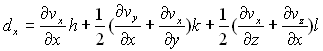
 où
où 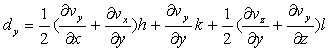
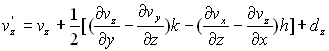 où
où 

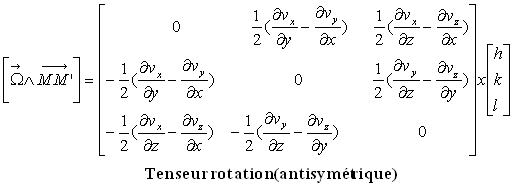

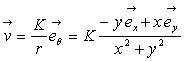

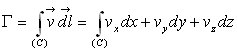
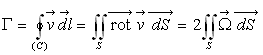 où
où
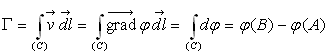 La circulation
du vecteur vitesse est indépendante du chemin suivi pour un écoulement
potentiel.
La circulation
du vecteur vitesse est indépendante du chemin suivi pour un écoulement
potentiel.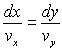 ð
ð 
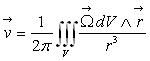
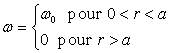
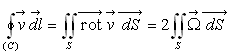 (analogue du
théorème d’Ampère en Magnétostatique),
(analogue du
théorème d’Ampère en Magnétostatique),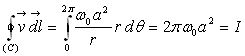 (intensité
du tourbillon).
(intensité
du tourbillon).
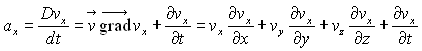 ð
ð
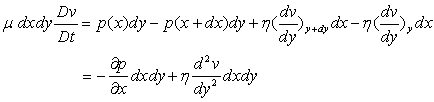
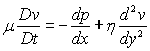
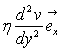 apparaît comme la densité volumique des forces de viscosité.
apparaît comme la densité volumique des forces de viscosité.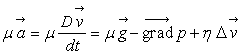
 le tenseur des contraintes visqueuses est un tenseur symétrique
le tenseur des contraintes visqueuses est un tenseur symétrique ;
; 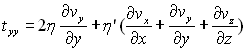 ;
;

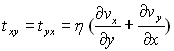 ;
; 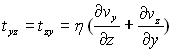 ;
;
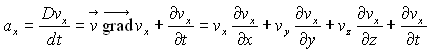
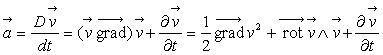 où
où 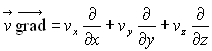 est un opérateur.
est un opérateur.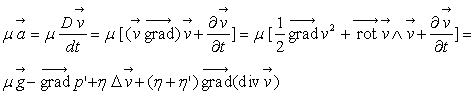 est l’équation de la dynamique des fluides dite de Navier pour
un fluide newtonien dans le seul champ de forces extérieures de pesanteur.
est l’équation de la dynamique des fluides dite de Navier pour
un fluide newtonien dans le seul champ de forces extérieures de pesanteur.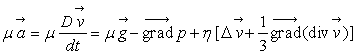 .
.
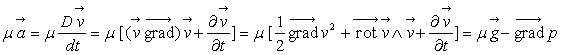

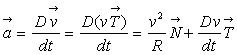 où
où 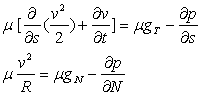

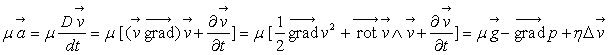
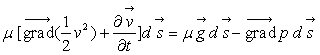 ð
ð
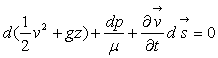
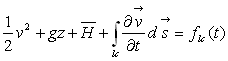 où la " constante " d’intégration
où la " constante " d’intégration 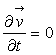 ð
ð 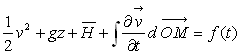 où la " constante " d’intégration
où la " constante " d’intégration 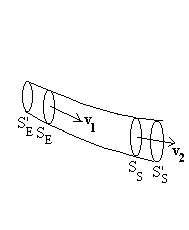

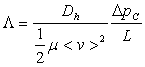 où
où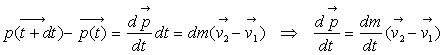
 .
.