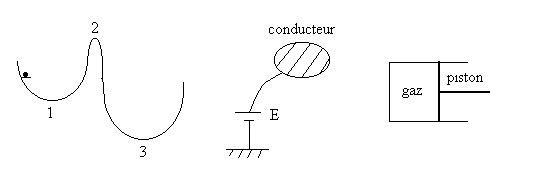
Le second principe de la Thermodynamique. Entropie (Notion d’extremum en Sciences Physiques)
Plan
1. Les lois en Physique
2. Minimum de la fonction potentielle. Minimum d'échange
d'énergie dans une transformation
3. Le Second Principe de la Thermodynamique
3.1. Le Second Principe pour un système fermé
3.2. Les énoncés historiques de Clausius
et Thomson
3.3. Les causes d'irréversibilité
Annexe : Clausius, Thomson, Carnot sur les traces du
second principe
La Physique est née du désir des hommes d’expliquer les
phénomènes naturels qui, nombreux et divers, nous paraissent,
lors de la première observation, parfois liés et plus souvent
éparpillés, indépendants, juxtaposés.
Nous sommes suffisamment avancés pour avoir conscience de cohérences,
de liens.
La Physique s’appuie, sur un petit nombre de modèles :
- celui de la particule et de l’hypothèse atomique,
- celui de l’onde,
sur la notion d’interactions et le concept d’énergie.
Parce que, sans aucun doute, il faut une bonne culture en Physique dite classique pour aborder les concepts d’une Physique dite moderne née au début du 19ème siècle, nous avons, à peine effleuré les liens entre l’espace et le temps, pas du tout ceux énergie et masse et senti, à travers la lumière que nous avons tantôt considérée comme une onde et tantôt comme une particule qu’il y avait beaucoup plus à dire dans le domaine de la dualité onde-corpuscule.
Une préoccupation constante du Physicien est de savoir si les
phénomènes obéissent à des lois générales.
Avec l’invariance galiléenne (covariance des lois par
changement de référentiels galiléens), Einstein a
fixé un critère de lois possibles.
Moins sensible ou moins en évidence dans nos choix de présentation
que le concept d’énergie, un autre concept est apparu : celui de
l’existence d’extremum.
Ainsi, le trajet (principe de Fermat) suivi par la lumière pour
aller d’un point à un autre est tel que le temps mis soit minimal.
Rectiligne dans un milieu d’indice constant (distance minimale), courbe
dans un milieu d’indice variable pour respecter le principe de Fermat,
certains disent que le trajet suivi par la lumière est celui qui
lui paraît le plus " facile ", de moindre " résistance ".
Nous n’avons pas étudié la Conduction de la Chaleur qui
est une propagation d’onde de matière, nous ne l’avons pas fait
ressortir à propos des lignes de courant électrique mais
nous retrouvons la même proposition à savoir les lignes de
flux de chaleur ou les lignes de courant électrique sont des lignes
de moindre résistance.
La Mécanique de Lagrange, conçue à partir
des notions d’énergie cinétique et potentielle, s’appuie
sur la notion de fonction extrémale et définit un principe
de moindre action.
2. Minimum de la fonction potentielle. Minimum d’échange d’énergie dans une transformation
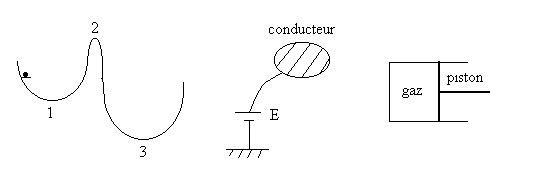
Dans le chapitre " Dynamique du point ", nous avons montré que,
pour un équilibre stable c’est à dire naturel, l’énergie
potentielle est minimale.
Nous prenons l’exemple du dessin de gauche et de l’énergie potentielle
de pesanteur pour mieux comprendre le propos précédent.
La bille est posée sur un taquet, contrainte à rester.
Si nous la libérons, elle atteindra la position 1 d’équilibre
stable (naturel) et d’énergie potentielle moindre que dans la position
d’équilibre contraint. On remarquera le rôle du frottement
indispensable pour se stabiliser en position 1.
Si nous sommes capables de faire passer à la bille le sommet
2 (la barrière de potentiel 2), elle s’équilibrera dans la
position d’équilibre naturel 3 d’énergie potentielle moindre
qu’en 1.
Imaginons qu’un opérateur extérieur fasse passer un objet de masse
m d’une position d’équilibre d’altitude ![]() à une position d’équilibre d’altitude
à une position d’équilibre d’altitude ![]() (
(![]() ). Pour ce faire
il dépense un travail
). Pour ce faire
il dépense un travail ![]() .
.
L’ égalité est obtenue :
- dans le cas " d’école " où il n’y a pas de frottement
(sans intérêt),
- dans le cas où , à chaque instant, l’opérateur
exerce une force opposée et d’intensité juste supérieure
(à la limite égale) au poids ; La vitesse de déplacement
de l’objet entre les deux positions d’équilibre est voisine de zéro
(à la limite " nulle "). L’objet à chaque instant est voisin
d’un état d’équilibre, la transformation est quasistatique.
Ce cas montre que le travail dépensé par l’opérateur
pour emmagasiner une énergie potentielle est minimal dans une transformation
quasistatique.
Ce type de conclusion est général, prenons l’exemple électrique
du dessin ci-dessus où nous portons un conducteur à potentiel
E. Son énergie potentielle électrique est égale
à ![]() .
.
Quelle énergie a fourni le générateur ?
- Si le générateur a une différence de potentiel constante
égale à E, il fournira ![]() charges à potentiel E, soit une énergie égale à
charges à potentiel E, soit une énergie égale à ![]() et la moitié de l’énergie délivrée par le générateur
n’aura pas été emmagasinée dans le conducteur sous forme
d’énergie potentielle électrique. A chaque instant de la transformation,
il y a déséquilibre des potentiels entre celui E
du générateur et celui V du conducteur, les charges électriques
s’écoulent par le fil électrique à vitesse non nulle ;
il y a donc courant électrique et effet Joule du à une résistance
du milieu au mouvement des charges.
et la moitié de l’énergie délivrée par le générateur
n’aura pas été emmagasinée dans le conducteur sous forme
d’énergie potentielle électrique. A chaque instant de la transformation,
il y a déséquilibre des potentiels entre celui E
du générateur et celui V du conducteur, les charges électriques
s’écoulent par le fil électrique à vitesse non nulle ;
il y a donc courant électrique et effet Joule du à une résistance
du milieu au mouvement des charges.
- Si nous voulons éliminer l’effet Joule, il convient d’avoir
un générateur de force électromotrice variable de
façon qu’à chaque instant force électromotrice et
potentiel du conducteur soient proches (à la limite égaux)
; Il y aura " équilibre à chaque instant ", la transformation
sera quasistatique.
Nous prenons maintenant l’exemple du gaz que l’on comprime d’une pression initiale ![]() à une pression
à une pression ![]() .
.
Sans rien enlever à la généralité de notre propos,
nous supposons la transformation isotherme c’est à dire le récipient
contenant le gaz en contact thermique avec une source de chaleur à température
constante ![]() ,
nous supposons linéaire le déplacement du piston et assimilons
le gaz à un gaz parfait.
,
nous supposons linéaire le déplacement du piston et assimilons
le gaz à un gaz parfait.
Supposons que l’opérateur extérieur applique la pression ![]() dès le début de la transformation.
dès le début de la transformation.
Il y a déséquilibre de pression entre l’extérieur
et le gaz à chaque instant de la transformation qui est irréversible.
Le travail élémentaire reçu par le gaz de la part de l’opérateur
extérieur est égal à ![]() et
le travail total reçu sera
et
le travail total reçu sera ![]() .
.
Supposons maintenant que l’opérateur applique la pression ![]() progressivement de façon qu’à chaque instant pression extérieure
et pression du gaz soient voisines. La transformation est quasi statique.
progressivement de façon qu’à chaque instant pression extérieure
et pression du gaz soient voisines. La transformation est quasi statique.
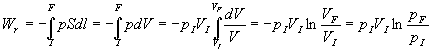
Or ![]() quelques
soient
quelques
soient ![]() ð
ð![]() .
.
3. Le Second Principe de la Thermodynamique
Le Second Principe (appelé en France Principe de S. Carnot) est né, au début de l’ère industrielle entre 1810 et 1860 des réflexions menées sur le fonctionnement des machines thermiques. En fait, outre S. Carnot, il convient de citer les travaux de R. Clausius, G.A. Hirn et W. Thomson anobli en Lord Kelvin.
L’expérience montre que certaines transformations qui satisferaient le Premier Principe ne se produisent pas, par exemple,
Les raisonnements qui ont permis une formulation générale
à partir de ces premières observations sont délicats
et, depuis le milieu du 19ème siècle, il a été
l’objet de nombreuses recherches, en particulier son interprétation
statistique a largement contribué au développement d’idées
apparues au début du 20ème siècle.
Ainsi actuellement, le Second Principe dépasse largement un
cadre d’applications liées aux machines et nous adopterons une présentation
axiomatique inspirée par les travaux d’I. Prigogine dans les années
1950.
Cette démarche pédagogique fait apparaître les
énoncés de Clausius ou Thomson, le fonctionnement des machines
thermiques comme des conséquences justificatrices de la validité
du Second Principe.
Si nous voulons croire à des lois générales en
Physique, il nous faut chercher, pour expliquer cette évolution
d’un système (constitué de deux sous-systèmes) isolé
vers un état d’équilibre défini, l’existence d’une
fonction pour le système qui serait extrémale
pour cet état d’équilibre.
La notion de minimum ou de maximum est relative puisqu’il suffit
de changer le signe dans la définition de la fonction pour changer
la nature de l’extremum.
Le problème posé est analogue à celui, en Mécanique,
de la position relative d’équilibre stable de deux solides constituant
un système mécanique isolé : cette position d’équilibre
est telle que l’énergie potentielle d’interaction entre les deux
solides est minimale.
Le second principe de la Thermodynamique postule l’existence de cette
fonction et l’appelle entropie. Sa notation habituelle est S.
La fonction entropie S est maximale pour un système
thermodynamique isolé.
Certains scientifiques rares préconisent l’introduction d’une fonction ![]() appelée négentropie pour que l’extremum soit un minimum ; ceci
n’a pas une grande importance.
appelée négentropie pour que l’extremum soit un minimum ; ceci
n’a pas une grande importance.
Par contre, et cela est beaucoup plus important, la fonction entropie
s’interprète au niveau microscopique. Il ne faut pas s’en étonner,
l’énergie interne se visualise au niveau microscopique, l’état
d’équilibre entre deux solides en interaction correspond au minimum
de l’énergie d’interaction entre ces deux solides c’est à
dire à une interprétation interne au deux solides.
Ce qui est plus délicat, c’est qu’on ne peut visualiser l’entropie
au niveau microscopique sans comprendre ce qu’est un état quantique,
sans être capable de dénombrer ces états quantiques
…et nous ne pouvons le faire sans connaissances réelles en Physique
statistique.
3.1. Le Second Principe pour un système fermé
3.1.1. Enoncé
A tout système est associée une fonction d’état
appelée entropie et notée S.
L’entropie est une grandeur additive.
Au cours d’une transformation d’un système fermé la variation
d’entropie d’un état initial à un état final est égale
à :
![]()
Nous limiterons nos propos à des sources de chaleur à
température uniforme.
Si dQ est la quantité de chaleur échangée
par le système entre les instants t et t + dt avec une
source à température TS,
l’entropie dSe
échangée sera : ![]()
Si, entre les instants t et t + dt, dQ
est la quantité de chaleur échangée avec la (les)
source(s), T la température commune, alors d
Se
= d
Q / T.
Comme Sc = 0, on obtient ![]() ,
ou en intégrant
,
ou en intégrant 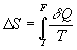 .
.
Remarque : l’unité légale de mesure de l’entropie est
le Joule/Kelvin (![]() ).
).
3.1.2. Entropie d’un système isolé fermé
Un système isolé hors d’équilibre évolue
vers un état d’équilibre " naturel ou non-contraint ", c’est
à dire vers un état d’équilibre qui n’est pas imposé
par l’action du milieu extérieur.
L’écriture du second principe montre que l’entropie est maximale
puisque celle-ci augmente pendant l’évolution vers l’état
d’équilibre … ce qui est conforme à nos propos initiaux.
3.1.3. Conséquences mathématiques des premier et second principes
Nous avons introduit deux fonctions d’état U et S (trois
avec l’enthalpie![]() mais cette dernière se déduit directement de U ou inversement)
, leurs variations sont indépendantes de la transformation et ne dépendent
que des états initial et final.
mais cette dernière se déduit directement de U ou inversement)
, leurs variations sont indépendantes de la transformation et ne dépendent
que des états initial et final.
Nous disposons de deux méthodes pour calculer ces variations,
- connaître une transformation quelconque entre état initial
et état final et faire le calcul,
- connaître les fonctions d’état et exprimer leurs variations.
Connaissance de U (ou H) et S
Nous apprendrons que les formes différentielles d
W
+ d
Q et dQ/
T d’un système sont connues.
Ces formes différentielles sont respectivement, selon les premier
et second principes, les différentielles dU et dS
des fonctions U et S.
Les Mathématiques nous apprennent que des formes différentielles
de ce type sont des différentielles totales exactes qui possèdent
des propriétés remarquables, en particulier celle d’obéir
au critère de Cauchy.
Cet aspect mathématique de la Thermodynamique sera traité
au chapitre " Transferts d'énergie. Propriétés de
la matière. Bilans énergétiques " en s’appuyant sur
l’annexe " Eléments de Mathématiques " en fin de l’ouvrage.
Calcul de Sc
Ce calcul ne peut être fait qu’à partir de ![]() .
.
3.2. Les énoncés historiques de Clausius et Thomson
3.2.1. Enoncé de Clausius
" La chaleur ne passe pas spontanément d’un corps froid sur un
corps chaud "
Considérons un système ![]() isolé thermiquement constitué de deux sous-systèmes
isolé thermiquement constitué de deux sous-systèmes ![]() et
et ![]() de températures
respectives
de températures
respectives ![]() échangeant entre eux uniquement de l’énergie thermique.
échangeant entre eux uniquement de l’énergie thermique.
Nous nous plaçons entre les instants t et ![]() où nous pouvons considérer
où nous pouvons considérer ![]() et
et ![]() fixées,
nous notons
fixées,
nous notons ![]() et
et ![]() les échanges
de chaleur respectivement aux systèmes
les échanges
de chaleur respectivement aux systèmes ![]() et
et ![]() .
.
L’isolation thermique de ![]() conduit à
conduit à ![]() et à
et à ![]() puisque le système
puisque le système ![]() n’échange pas de chaleur.
n’échange pas de chaleur.
Le caractère additif de l’entropie permet d’écrire aussi ![]()
Le calcul de ![]() ou
ou ![]() ne nécessite
pas de connaître la transformation, il convient de respecter état
initial et état final.
ne nécessite
pas de connaître la transformation, il convient de respecter état
initial et état final.
Ainsi pour le système ![]() (ou
(ou ![]() ) à
température
) à
température ![]() (ou
(ou ![]() ), nous
pouvons imaginer qu’il a échangé
), nous
pouvons imaginer qu’il a échangé ![]() (ou
(ou ![]() ) dans
une transformation réversible c’est à dire avec une source à
température
) dans
une transformation réversible c’est à dire avec une source à
température ![]() (ou
(ou ![]() ).
).
![]() et
et ![]()
Soit ![]()
ce qui entraîne ![]() .
.
La chaleur passe spontanément du corps chaud sur le corps
froid.
Remarque : nous aurions pu raisonner à partir du seul système ![]() (ou du seul système
(ou du seul système ![]() )
et nous aurions trouvé, évidemment, des résultats identiques
; par contre nous ne sommes pas capable d’affecter l’entropie créée
par irréversibilité, l’exercice du mur (voir ci-après dans
le paragraphe 3) montre que cette entropie d’irréversibilité est
principalement créée dans le système " séparant
" les systèmes
)
et nous aurions trouvé, évidemment, des résultats identiques
; par contre nous ne sommes pas capable d’affecter l’entropie créée
par irréversibilité, l’exercice du mur (voir ci-après dans
le paragraphe 3) montre que cette entropie d’irréversibilité est
principalement créée dans le système " séparant
" les systèmes ![]() et
et ![]() .
.
3.2.2. Enoncé de Thomson
" Un système en contact avec une seule source de chaleur ne peut,
au cours d’un cycle, que recevoir du travail et fournir de la chaleur "
Le premier principe s’écrit 0 = W + Q
Le second principe s’écrit 0 = Q / TS
+ Sc
ce qui entraîne ![]()
Généralement, on exprime ce résultat par la phrase
:
"avec une seule source de chaleur, on ne peut réaliser une
machine thermique motrice".
3.3. Les causes d’irréversibilité
Exemple d’irréversibilité : le transfert thermique
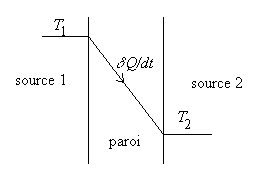 |
Une source de chaleur 1 à température
constante T1 fournit de la chaleur
à une source de chaleur 2 à température constante
T2
(T1 > T2
). Le contact thermique est assuré par une simple paroi solide.
Si les deux sources sont des fluides nous sommes dans le cas d’un échangeur.
Nous nous situons en régime permanent et considérons comme système la paroi. Ce système est en état de déséquilibre, cependant les variables d’état gardent des valeurs constantes en chaque point. |
Par suite la variation d’entropie au cours du temps sera nulle (DS = 0). Le système échange de la chaleur, donc de l’entropie, avec chacune des sources. Il reçoit, par unité de temps, l’énergie calorifique dQ / dt de la part de la source à température T1 qu’il perd avec celle à température T2 .
![]()
Le transfert thermique qui a lieu spontanément des parties
chaudes vers les parties froides est une cause importante d’irréversibilité.
Les causes d’irréversibilité
Annexe : Clausius, Thomson, Carnot sur les traces du second principe
Clausius : " La chaleur ne passe pas spontanément d’un corps
froid sur un corps chaud "
En d’autres termes, pour faire passer de la chaleur d’un corps froid vers un
corps chaud (corps de température plus élevée), il faut
une intervention extérieure aux deux corps (machine qui modifiera le
milieu extérieur).
Supposons la proposition inverse vraie et considérons deux corps 1 et
2 à même température ![]() .
Pour une cause fortuite, imaginons un léger déséquilibre
tel que la température du corps 2 devienne très légèrement
inférieur à celle du corps 1. Si nous supposons que la chaleur
passe spontanément du corps froid sur le corps chaud, alors nous sommes
capables d’accentuer le déséquilibre et d’obtenir deux sources
de chaleur telles que
.
Pour une cause fortuite, imaginons un léger déséquilibre
tel que la température du corps 2 devienne très légèrement
inférieur à celle du corps 1. Si nous supposons que la chaleur
passe spontanément du corps froid sur le corps chaud, alors nous sommes
capables d’accentuer le déséquilibre et d’obtenir deux sources
de chaleur telles que ![]() .
.
Or, avec deux sources de chaleur, Clausius, Thomson et Carnot savaient qu’on
était capable de faire un moteur (machine à vapeur).
Conclusion : A partir d’une seule source de chaleur (![]() ),
on a finalement réalisé un moteur ce qui est contraire à
l’énoncé de :
),
on a finalement réalisé un moteur ce qui est contraire à
l’énoncé de :
Thomson : " Un système en contact avec une seule source de chaleur
ne peut, au cours d’un cycle, que recevoir du travail et fournir de la chaleur
"
Supposons que nous ayons une seule source de chaleur (que nous séparons
en deux parties -sources- notées 1 et 2 de même température).
Imaginons que l’énoncé de Thomson soit faux : avec la source 1
nous sommes capable de faire un moteur ce qui veut dire que la partie 1 a produit
du travail à l’extérieur. En conséquence, la partie 1 a
reçu de la chaleur et sa température ![]() augmente. Cette chaleur a été perdue par la partie 2 et sa température
augmente. Cette chaleur a été perdue par la partie 2 et sa température ![]() diminue.
diminue.
Conclusion : A partir d’une seule source de chaleur (![]() ),
nous avons fait, sans intervention du milieu extérieur, passer de la
chaleur du corps froid sur le corps chaud ce qui est contraire à l’énoncé
de Clausius.
),
nous avons fait, sans intervention du milieu extérieur, passer de la
chaleur du corps froid sur le corps chaud ce qui est contraire à l’énoncé
de Clausius.
Ainsi, si la proposition de Clausius est fausse, celle
de Thomson est aussi fausse et inversement.
Il y a donc équivalence entre les énoncés
de Clausius et Thomson.
Cycle monotherme
a) irréversible
L’énoncé de Thomson implique ![]() Þ
Þ![]() puisque
puisque ![]() .
.
Le système a fourni de la chaleur a la source.
b) réversible
Les transformations étant réversibles, on peut envisager de décrire
dans un sens 1 et dans le sens 2 en passant par les mêmes états
d’équilibre ce qui entraîne ![]() .
.
Or nous savons que ![]() .
.
Ces trois propositions simultanément vérifiées impliquent
: ![]() Þ
Þ![]() .
.
Cycle ditherme
Une machine 1 échange avec deux sources (Q1
avec une source chaude à température q1
; Q2 avec une source chaude à
température q2
) ainsi qu’un travail W (![]() ).
).
Une deuxième machine échangent avec les deux mêmes sources
(Q’1 avec une source chaude à
température q1
; Q’2 avec une source chaude à
température q2
) ainsi qu’un travail W’ ![]() .
.
La taille de la deuxième machine et le sens des évolutions sont
tels que ![]() .
.
Si nous considérons la machine ensemble des deux machines, elle
n’échange pas avec la source froide : elle est équivalente
à une machine monotherme.
a) réversible
Théorème de Carnot : Le rendement de toutes
les machines dithermes réversibles (appelées machines de Carnot
est le même.
Le rapport ![]() ne dépend pas de la machine, il ne dépend que des températures
des sources chaude et froide Þ
ne dépend pas de la machine, il ne dépend que des températures
des sources chaude et froide Þ![]()
Par définition, la fonction g est appelée température
thermodynamique ![]() .
.
Soit, ![]()
 |
On montre sans difficulté, que :
|
b) irréversible
Avec les deux sources à températures ![]() et
et ![]() , on envisage
le fonctionnement de deux machines, l’une où les transformations sont
irréversibles (machine ditherme irréversible ;
, on envisage
le fonctionnement de deux machines, l’une où les transformations sont
irréversibles (machine ditherme irréversible ; ![]() ),
l’autre où les transformations sont réversibles (machine ditherme
réversible ou machine de Carnot ;
),
l’autre où les transformations sont réversibles (machine ditherme
réversible ou machine de Carnot ; ![]() )
dimensionnées de telle sorte que
)
dimensionnées de telle sorte que ![]() .
.
L’ensemble des deux machines est une machine monotherme irréversible
avec la source à température ![]()
Þ![]() et
et ![]() .
.
D’autre part, pour un cycle de Carnot, nous savons que ![]() (ou
(ou ![]() )
)
Soit, ![]() Þ
Þ![]() (ou
(ou ![]() )
)
Complément au théorème de Carnot : ![]()
Le rendement d’une machine fonctionnant suivant un cycle ditherme irréversible
est inférieur au rendement d’une machine fonctionnant suivant un
cycle ditherme réversible (cycle de Carnot) entre les deux mêmes
source de chaleur.
Notion d’entropie et second principe de la Thermodynamique
Pour un cycle de Carnot nous avons trouvé : ![]()
Pour un cycle ditherme irréversible : ![]()
Ces résultats sont facilement généralisables (il convient
d’envisager une succession de machines) à des cycles polythermes (plusieurs
sources à températures ![]() ).
).
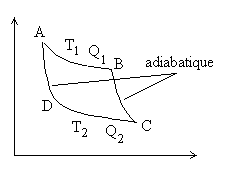
Ainsi, pour un cycle polytherme irréversible : 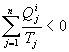
et, pour un cycle polytherme réversible : 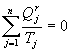
Dans le cas de la réversibilité, la condition d’équilibre
thermique impose à la température de la source en contact avec
le fluide (système) de la machine d’être égale à
la température du fluide (![]() ).
).
On peut alors écrire : 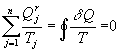 où
où ![]() est la quantité de chaleur élémentaire échangée
par le fluide à l’instant considéré.
est la quantité de chaleur élémentaire échangée
par le fluide à l’instant considéré.
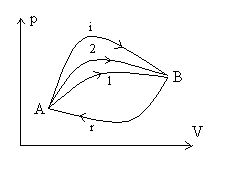 |
Les transformation 1, 2 , r sont réversibles,
la transformation i est irréversible.
Þ |
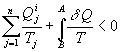
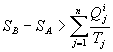 où on appelle entropie échangée la quantité
où on appelle entropie échangée la quantité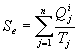
Ainsi, ![]() où
on appelle entropie créée la quantité
où
on appelle entropie créée la quantité ![]() .
Cette quantité est positive dans le cas d’une transformation irréversible,
elle est nulle pour une transformation réversible.
.
Cette quantité est positive dans le cas d’une transformation irréversible,
elle est nulle pour une transformation réversible.
Ce résultat constitue le second principe de la Thermodynamique.