sont deux lentilles minces, convergentes, de même axe optique. On désigne
par 
la distance
focale de la lentille 
Exercices d’optique ondulatoire
1) On considère le dispositif interférentiel
des fentes d’Young ci-dessous où
sont deux lentilles minces, convergentes, de même axe optique. On désigne
par la distance
focale de la lentille
|
|
Au foyer objet de la lentille |
On examine les phénomènes qui se produisent dans
le plan focal image 
de la lentille 
.
On appelle 
l’abscisse
d’un point 
de
ce plan par rapport au foyer image 
.
1)1) La source émet deux radiations dont les longueurs d’onde
respectives sont 
et 
.
Qu’observe t’on dans le plan 
?
(on expliquera comment traiter le phénomène de diffraction)
En quels " points " du plan
le système de franges est-il complètement brouillé ?
1)2)a)
On suppose maintenant que :
,
, est égale
à 
. En quels
" points " du plan ,
l’éclairement paraît-il uniforme (le phénomène d’interférence
est négligeable) ?
où 
représente
la différence de temps de marches des deux rayons en 
.
Interpréter physiquement ce résultat en introduisant la durée
d’émission de la source.
| Réponse 11 | Réponse 12a | Réponse 12b |
2) On considère le dispositif interférentiel
des fentes d’Young ci-dessous où
sont deux lentilles minces, convergentes, de même axe optique. On désigne
par 
la distance
focale de la lentille .
|
|
Au foyer objet de la lentille |
On examine les phénomènes qui se produisent dans
le plan focal image
de la lentille .
On appelle l’abscisse
d’un point de
ce plan par rapport au foyer image .
2)1) La source émet une radiation de longueur d’onde 
.
Qu’observe t’on dans le plan ?
(on expliquera comment traiter le phénomène de diffraction)
2)2) On intercale, sur le trajet de l’un des faisceaux, une lame à
faces parallèles (épaisseur 
;
).
Déterminer le nombre 
de franges qui ont défilé en .
2)3) A partir de cette position on tourne la lame d’un angle 
.
Sachant que l’on peut apprécier au mieux le déplacement de 0,1
frange, avec quelle précision peut-on régler la position de la
lame ?
| Réponse 21 | Réponse 22 | Réponse 23 |
3) On considère le dispositif interférentiel
des fentes d’Young ci-dessous où 
est une lentille mince, convergente, de distance focale 
.
|
|
Au foyer objet de la lentille |
On examine les phénomènes qui se produisent dans
un plan 
à
distance 
de
l’écran.
3)1) Déterminer la valeur de 
pour laquelle le système de franges disparaît pour la première
fois ?
3)2) Pour 
donné, calculer l’intensité 
ainsi que le contraste.
| Réponse 31 | Réponse 32 |
4) On considère le dispositif interférentiel
ci-dessous où
sont deux lentilles minces, convergentes, de même axe optique. On désigne
par 
la distance
focale de la lentille .
|
|
Au foyer objet de la lentille
|
4)1) La source lumineuse est monochromatique de longueur
d’onde 
. Le diaphragme
est constitué
par deux fentes identiques, de largeur 
,
" infiniment longue ", parallèles entre elles, dont
les centres sont distants de 
.
Le dispositif ainsi étudié est un dispositif interférentiel
classique de fentes Young avec diffraction dans la direction 
.
Déterminer l’intensité lumineuse 
.
4)2)
Le diaphragme est un réseau par transmission dont 
désigne le nombre total d traits (ou de fentes). Ce réseau est
caractérisé par son pas 
,
distance entre les centre de deux traits (ou deux fentes) successifs.
, largeur d’une
fente (ou d’un trait), est très inférieur à 
.
4)2)a) Pourquoi l’intensité lumineuse est inchangée si
on intervertit largeur du trait et largeur de la fente.
4)2)b) Pour la source lumineuse, monochromatique de longueur d’onde ,
déterminer et représenter l’intensité lumineuse .
4)2)c) La source lumineuse émet deux longueurs d’onde voisines
.
Décrire le phénomène observé.
On considère que deux images sont distinctes l’une de l’autre (critère
de Lord Rayleigh) si le maximum principal d’intensité lumineuse correspondant
à 
coïncide
avec le minimum le plus voisin du maximum principal correspondant à 
(ou inversement).
En déduire le pouvoir de résolution 
du réseau.
A.N. 
;
Déterminer le pouvoir de résolution pour le premier ordre.
4)3) On observe uniquement dans le premier ordre d’interférence.
Déterminer l’intervalle spectral 
correspondant, dans le plan focal de la lentille 
,
à une distance 
des maxima de lumière.
Le montage réalisé constitue le schéma de base d’un spectroscope
à réseau. La quantité 
déduite de la question précédente caractérise la
dispersion du système. On l’exprime, en général, en Angströms
par millimètre.
Déterminer, en 
,
la dispersion du montage réalisé, la distance focale de
étant 
.
4)4) On utilise maintenant une source de lumière blanche s’étendant
de 
à
.
Déterminer la longueur occupée dans le plan d’observation par
les spectres des trois premiers ordres.
Quelle difficulté va-t-on rencontrer dans l’interprétation du
spectre si on observe dans les ordres supérieurs au premier ?
En se limitant au premier ordre, l’approximation de Gauss (angles petits) est-elle
valable dans tout le domaine 
.
| Réponse
41 | Réponse
42a | Réponse
42b | Réponse
42c | Réponse
43 | Réponse
44 |
|
5) On considère le dispositif ci-contre
constitué à partir de |
|
5)1) Montrer que l’amplitude 
diffractée par le système, dans la direction 
,
(
appartient
au plan de symétrie du système) peut se mettre sous la forme d’un
produit de deux fonctions caractéristiques, l’une pour la diffraction,
l’autre pour l’interférence.
En déduire, pour 
petit, les valeurs 
correspondant à des maxima de lumière. Qu’observe-t-on ?
5)2) On donne 
.
Déterminer le pouvoir de résolution 
de l’appareil.
5)3) On considère une lumière comportant un spectre centré
sur 
et de largeur
.
A partir de quelle valeur 
,
il y a-t-il recouvrement d’ordre (au voisinage de 
) ?
| Réponse 51 | Réponse 52 | Réponse 53 |
6) On dispose de l’huile de cèdre transparente
d’indice 
entre
deux lames de verre identiques dont les faces en regard 
et 
semi-argentées
sont parallèles, leur distance étant égale à 
.
On éclaire l’ensemble sous incidence normale par un faisceau de lumière
monochromatique de longueur d’onde 
.
Les faces et
on le même
facteur de réflexion 
et de transmission 
pour les intensités lumineuses (
).
L’œil est placé au foyer image d’un objectif 
qui lui permet de mettre au point dans un plan 
quelconque situé entre
et . L’intensité
lumineuse incidente sera prise comme intensité de référence.
|
|
Pour la compréhension de la figure et des réflexions
successives, les rayons sont représentés inclinés :
ils sont, en fait, perpendiculaires aux lames de verre ( |
6)2) On interpose dans l’huile des objets transparents
que l’on veut examiner en contraste interférentiel. Ces objets 
,
d’épaisseur faible 
,
sont assimilés à des petites lames à faces parallèles
d’indice 
voisin
de 
. L’œil effectue
la mise au point sur le plan d’un objet .
|
6)2)a) Donner la valeur du nouveau déphasage
|
|
6)2)d) Calculer la valeur de 
pour une épaisseur donné 
telle que 
(
entier positif ou nul).
Les objets sont-ils
visibles sachant que l’observation nécessite un contraste minimum de
l’ordre de 0,1 ?
On donne : 
;
; 
;
6)2)e) Pour une variation 
fixée, montrer que la valeur maximale du contraste vaut : 
.
Calculer, dans ce cas, l’épaisseur minimale 
observable.
| Réponse
61 | Réponse
62a | Réponse
62b | Réponse
62c | Réponse
62d | Réponse
62e |
|
7) On considère un réseau plan |
|
Le réseau s’étend selon 
de 
à
. Déterminer
la répartition d’amplitude dans le plan 
.
7)2) On suppose 
.
En déduire l’éclairement dans le plan
et expliquer ce que l’on observe.
| Réponse 71 | Réponse 72 |
8) Sur un axe 
,
on considère une source lumineuse monochromatique ponctuelle 
.
Un système optique, non absorbant, non déphasant et de grandissement
unité, en fournit deux images 
telles que soit une médiatrice
de 
. La distance
est égale
à 
.
sont des sources
secondaires émettant des vibrations lumineuses cohérentes 
.
On observe les interférences produites par ce dispositif dans un plan
(
) perpendiculaire
à en 
,
situé à distance 
de la droite
telle que 
. On
repère la position d’un point 
appartenant à ()
par ses coordonnées 
dans un repère d’origine ,
l’axe 
étant
parallèle à .
8)1)a) Montrer que l’intensité lumineuse en 
voisin de peut
se mettre sous la forme 
,
étant
l’interfrange que l’on définira et calculera.
8)1)b) On déplace la source
parallèlement à 
de sorte que
subissent le même déplacement que .
Comment est modifié le système de franges ? Même question
si le déplacement de
a lieu, dans les mêmes conditions, parallèlement à .
8)2) La source
est maintenant un rectangle de centre 
(
sur ),
de hauteur 
suivant
un axe 
et de
largeur 
suivant
un axe 
;
Les axes 
sont
parallèles aux axes 
.
Le système optique donne de
deux images égales ,
situées dans un même plan, parallèle au plan contenant
et à même distance de l’axe ;
soit 
un point
de , 
ses images à travers le système optique restent toujours à
la même distance 
quel que soit le point 
(
étant
sur la médiatrice de 
parallèle à ). Soient
les coordonnées
de 
, 
émettent deux vibrations lumineuses identiques de la forme 
.
On pose 
.
On observe les interférences lumineuses produites par ce dispositif dans
le plan (
) défini à
la question 1).
8)2)a) Montrer que deux éléments homologues, de même
surface 
, centrés
aux points donnent
en de coordonnées
, une intensité
lumineuse de la forme 
où 
est
une quantité que l’on définira et exprimera en fonction de 
.
8)2)b) On suppose que 
.
Déterminer l’intensité produite en 
par l’ensemble de la source 
.
Donner l’expression du contraste défini par : 
Représenter les variations de 
en fonction de 
.
Décrire le phénomène observé lorsqu’on fait varier
.
Pour quelle valeur de ,
obtient-on la première disparition du système de franges ?
Retrouver sans calcul ce résultat.
| Réponse
81a | Réponse
81b | Réponse
82a | Réponse
82b |
|
9) Une fente rectangulaire, percée dans
un écran opaque, est éclairée par un faisceau monochromatique
(longueur d’onde
|
|
En déduire la valeur de la quantité 
où 
représente
l’intensité lumineuse au point (
)
du plan focal. Conclure.
9)2) On place en 
un cache rectangulaire dont les cotés sont parallèles à
la fente (dimensions : 
selon 
et 
selon 
).
On a 
et 
et donc 
.
9)2)1) Que peut-on dire de la nouvelle répartition d’intensité
?
9)2)2)
On translate le cache en le maintenant dans le plan de la fente : comment
est modifiée la figure de diffraction ?
| Réponse 91 | Réponse 921 | Réponse 922 |
10) On considère un prisme de verre, d’indice
, plongé
dans l’air et dont la section droite est un triangle équilatéral
de coté 
.
Pour une incidence 
particulière, les rayons qui traversent le prisme ont un trajet perpendiculaire
au plan bissecteur de trace 
.
La face 
est
entièrement éclairée par un faisceau de lumière
parallèle .
|
|
10)1) Optique géométrique Dans la suite du problème, on considèrera
10)1)b) Un rayon de faisceau considéré
pénètre dans le prisme au point |
On montrera que ce chemin optique est indépendant de
et qu’il s’exprime
en fonction de 
seulement.
10)2) Diffraction
10)2)1)a) On considère la face de sortie 
comme une ouverture diffractante et l’on se propose de calculer l’amplitude
de la vibration lumineuse diffractée suivant une direction faisant un
angle 
avec la
normale à la face sortie ; la direction 
correspond au rayon émergent de l’optique géométrique et
l’angle 
sera
considéré comme très petit.
|
|
Les vibrations diffractées suivant cette direction
par les points Calculer la différence de phase
|
Calculer l’amplitude résultante diffractée dans
la direction
par l’ensemble de la face de sortie du prisme. En déduire l’intensité
lumineuse 
dans
la direction .
On posera 
.
10)2)1)c) Calculer la direction 
suivant laquelle se situe le premier minimum pour la lumière diffractée.
10)2)2) Le prisme est en fait absorbant, si bien qu’après traversée
d’une longueur 
de verre, l’amplitude de la vibration lumineuse est multipliée par le
facteur 
;
est une constante
positive suffisamment grande pour que l’amplitude de la vibration du rayon traversant
le prisme dans sa plus grande épaisseur est négligeable.
10)2)2)a) Calculer l’intensité lumineuse 
diffractée dans la direction
par l’ensemble de la face de sortie du prisme. On posera 
.
10)2)2)b) Calculer la direction 
suivant laquelle l’intensité lumineuse est réduite de moitié.
10)2)3) Application numérique
; 
;
; 
Calculer successivement l’angle d’incidence 
,
les angles 
.
| Réponse 101a | Réponse 101b | Réponse 1021a | Réponse 1021b | Réponse 1021c | Réponse 1022a | Réponse 1022b |
11) Diffraction par des ouvertures circulaires
11)1) Une ouverture circulaire de rayon 
,
percée dans un écran opaque, est éclairée par un
faisceau monochromatique (longueur d’onde dans le vide 
)
cohérent, perpendiculaire au plan de l’écran.
Calculer l’intensité lumineuse (on appellera 
l’angle entre la direction incidente et la direction d’observation.
|
11)2) L’œil est assimilable à une lentille
(L) diaphragmée par une pupille circulaire de rayon |
|
En supposant que la diffraction est la seule cause de limitation
du pouvoir de résolution de l’œil, déterminer la valeur minimale
de 
pour laquelle
l’œil commence à séparer les deux points.
Données mathématiques
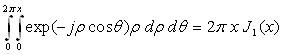
: fonction
de Bessel de 1ère espèce d’ordre 1 ; 
Le
premier zéro de 
est 
, le deuxième
est 
, le troisième
est 
, le …
| Réponse 111 | Réponse 112 |
,
on place un écran percé d’une fente très fine, éclairée
par une lampe située en amont (fente source 
).
identiques très fines, distantes de 
.
Les grands cotés de ces rectangles sont parallèles à
la fente source 
.
Le dispositif est dans l’air d’indice 
.
,
une fente source de largeur 
écran émet un radiation de longueur d’onde 
.
.
lames de verre (de même épaisseur 
,
d’indice 
,
décalées de 
).
On prendra 
.
)
tombant normalement sur la face d’entrée du système. On
supposera que les faces 
(largeur 
et longueur 
)
diffractent la lumière. (on ne tiendra pas compte d’éventuelles
réflexions à l’intérieur du verre)
).
et du déphasage 
entre deux rayons successifs.
en fonction de 
.
entre
deux rayons transmis consécutifs traversant l’objet 
due à la traversée de l’objet 
est petit, montrer que 
où 
sont des coefficients que l’on calculera en fonction de 
.
,
montrer que 
.
à transmission d’amplitude 
dont les " sillons " sont perpendiculaires à
l’axe 
)
de rayons parallèles issus d’une source ponctuelle.
.
)
cohérent, perpendiculaire au plan de l’écran.
d’une lentille mince convergente (distance focale 
).
:
.
en fonction de 
comme
une donnée au même titre que 
et 
.
(
).
où 
est le point du plan d’onde perpendiculaire au faisceau incident passant
par 
et
l’intersection
du rayon avec 
.
coupent respectivement en 
le plan d’onde passant par 
.
entre ces vibrations. Le résultat sera exprimé en fonction
de 
, de
, de 
et de 
(longueur d’onde de la lumière utilisée.
la vibration diffractée par un élément de surface
de largeur 
autour de 
dont la distance focale est 
.
L’indice optique sera pris égal à 
.
).