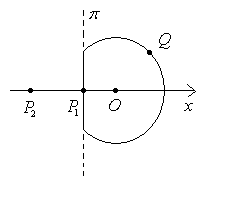Exercices Optique geometrique

Exercices d’Optique géométrique

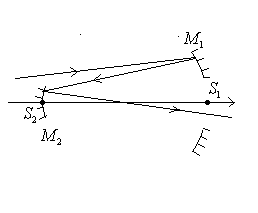
1) Stigmatisme rigoureux ; points de Weierstrass

On considère le système optique à symétrie axiale représenté sur la figure ci-contre. Une sphère, de rayon , d’indice , tronquée par un plan dont la distance au centre de la sphère est , est placée dans de l’air d’indice égal à 1.
On considère un rayon où est l’intersection du plan et de l’axe optique du système et le point où le rayon perce la sphère.
On appelle le point de l’axe optique distant de du centre de la sphère, appartenant au segment .

Comparer le chemin optique du rayon (situé dans la sphère) et le chemin optique du rayon (situé dans l’air). Conclusions.

| Réponse |

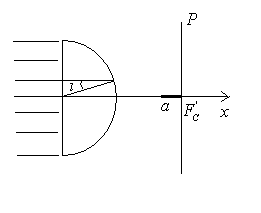
2) Approximation de Gauss

Un faisceau cylindrique de lumière monochromatique normal à la face plane d’une demi-boule en verre, de rayon 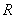, d’indice , couvre toute cette face

1) Du coté de la face de sortie, on observe le long de l’axe optique une portion lumineuse brillante.
Comment peut-on expliquer sa présence ? Exprimer sa longueur en fonction de et de .
2) On dispose un écran perpendiculairement à l’axe optique au foyer image .
Que voit-on sur cet écran ?
3) On limite le faisceau incident au voisinage de l’axe optique. Soit l’angle d’incidence sur la face sphérique du rayon le plus éloigné de l’axe.

Calculer la valeur maximale à admettre pour 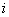si l’on ne veut pas que le rayon de la tache lumineuse dans le plan 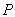excède quand et .

| Réponse 21 | Réponse 22 | Réponse 23 |

3) Aberration chromatique

Un système centré est constitué par un cylindre de verre, d’indice pour une radiation , terminé par deux faces sphériques convexes de rayons . L’épaisseur est .

Calculer en fonction de pour que la position du foyer image ne varie pas lorsque la longueur d’onde de la lumière varie légèrement.

| Réponse |

4) On considère une sphère de verre, d’indice 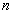, de rayon .
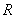Montrer que ce système optique appelé lentille-boule est équivalent à une lentille mince.
Comparer, du point de vue des aberrations monochromatiques, la lentille-boule à sa lentille mince équivalente de même verre.

| Réponse |

5) On considère une sphère de verre, d’indice 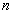, de rayon 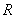, de centre dont l’une des faces est argentée.
Montrer que ce système optique est équivalent à un miroir dont on calculera les caractéristiques.

| Réponse |

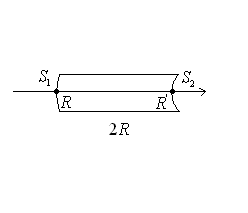
6) Soient deux lentilles-boules identiques, d’indice 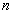, de rayon 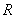, distantes de .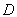
Trouver une condition sur 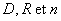pour que, dans les conditions de Gauss, le système soit afocal (l’axe optique est la droite passant par les centres des deux lentilles-boules).

| Réponse |

7) Prisme

On considère un prisme en verre d’angle et d’indice .
Soit l’angle d’incidence.
Calculer l’angle de déviation , angle entre rayon incident et rayon émergent.
Montrer que passe par un minimum ().
En déduire une méthode de mesure de l’indice .

| Réponse |

8) Mirage

On étudie la propagation d’un rayon lumineux dans un plan vertical où l’indice varie suivant la relation :
8)1) Montrer que :
8)2) En déduire l’équation différentielle de trajectoire du rayon lumineux :
Montrer que la trajectoire est une parabole

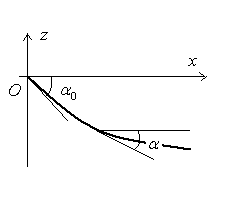
8)3) Montrer que cette théorie s’applique aux mirages (on justifiera la variation de l’indice 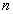d’un gaz avec l’altitude 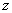à partir de la relation de Gladstone 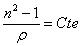où 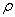est la masse volumique du gaz)

| Réponse 81 | Réponse 82 | Réponse 83 |

9) On considère l’ensemble des systèmes optiques constitués de deux miroirs sphériques (ou portions de miroirs sphériques) tels que les rayons utiles se réfléchissent sur le miroir (sommet , centre ) puis sur le miroir (sommet , centre ).

On pose : ; ; avec positifs.
1) Déterminer la position des foyers objet et image

2) On définit les points principaux , points conjugués pour lesquels le grandissement transversal est égal à 1.
Donner la valeur de .

3) En déduire les distances focales image () et objet (). A quelle condition le système est afocal.
Retrouver ce résultat directement.

| Réponse 91 | Réponse 92 | Réponse 93 |

10) A l’aide d’un objectif (assimilable à une lentille mince convergente 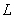de distance focale ), on désire former l’image d’un objet réel sur une plaque photographique située à une distance de l’objet.
1) Entre quelles valeurs peut varier 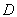pour qu’il en soit ainsi ? Préciser la distance séparant la lentille de la plaque photographique (on se limitera à ).
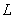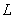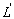2) La lentille convergente restant fixe par rapport à l’objet , on recule la plaque photographique et on intercale, entre la plaque et la lentille , une lentille divergente de distance focale .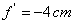
Comment doit-on placer 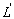pour que le grandissement linéaire du système soit multiplié par 2 ? De combien a t’il fallu déplacer la plaque photographique ?
3) Peut-on généraliser ce dispositif (grandissement linéaire multiplié par un facteur 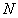donné) ?

| Réponse 101 | Réponse 102 | Réponse 103 |

11) Lunette de Galilée (extrait de Capes)

En 1610, Galilée témoigne de ses travaux concernant la lunette qui portera son nom :
" …Je me suis mis à penser aux moyens de fabriquer l’instrument. J’y parvins si parfaitement que j’en construisis un, formé d’un tube de fer, extérieurement recouvert d’un drap cramoisi et long d’environ trois quarts de coudée*, il comprenait deux lentilles de la grandeur d’un écu à chaque extrémité, l’une plan concave, contre laquelle on plaçait l’œil, l’autre plan convexe …"
* La coudée est une unité de mesure correspondant à 50 cm.

Lettre de Galilée à B. Landucci

" …Quel spectacle magnifique et passionnant que de voir le corps lunaire, éloigné de nous de presque soixante rayons terrestres, rapproché au point de nous sembler éloigné seulement de deux rayons : son diamètre nous apparaît ainsi trente fois plus grand …qu’à l’œil nu …"

adapté de Sidereus Nuncius, le Messager des Etoiles (Galilée)

1) Quelle est la nature des lentilles utilisées par Galilée ?

2) La lunette est réglée de façon à donner d’une étoile (objet à l’infini), une image à l’infini ce qui permet à l’observateur d’éviter toute fatigue puisqu’il voit sans accommodation. Dans ces conditions, la lunette est dite " afocale ".
2)1) Préciser et justifier la position des foyers dans une lunette " afocale ".
2)2) Réaliser un schéma, sans respecter les échelles, montrant le devenir d’un rayon incident faisant un angle avec l’axe optique et émergeant sous un angle dans les conditions de Gauss.
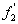2)3) Déterminer l’expression du grossissement de la lunette en fonction de distance focale de l’objectif et distance focale de l’oculaire.
2)4) Montrer, en utilisant le texte de Galilée, que le grossissement de sa lunette est à peu près égal à 30 ; en déduire les valeurs approximatives des distances focales et des vergences de chacune des lentilles utilisées.

3) Da haut du Campanile de Venise, les sénateurs vénitiens invités par Galilée, observent avec cette lunette en direction de Murano, distante de deux kilomètres et demi. Ils distinguent avec enthousiasme le mouvement des gens !
3)1) Sous quel angle les personnes de 1,70 m sont-elles observées à travers l’instrument ?
3)2) A quelle distance les sénateurs ont-ils, dans ces conditions, l’impression de voir les habitants de Murano, si l’on se réfère aux textes de Galilée reportés ci-dessus ?

12) Etude d’un appareil photographique (extrait de Capes)

L’objectif d’un appareil photo est modélisé par une lentille mince convergente de distance focale 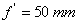, accolée à un diaphragme circulaire de diamètre 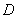. Les axes de la lentille et du diaphragme sont confondus.
La lentille est utilisée dans les conditions de Gauss.
On définit le nombre d’ouverture N par le rapport .

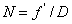1) Enoncer les conditions de Gauss.

2) La mise au point étant faite à l’infini, quelle est la distance de l’objectif au plan du film ?

3) La distance minimale de mise au point parfaite étant de 60 cm, calculer dans ces conditions la distance de l’objectif au plan du film. Commenter le résultat.

4) Notion de profondeur de champ
L’objectif est mis au point à l’infini. A tout point de l’axe correspond alors sur la pellicule une tache. Compte tenu du grain de la pellicule et de l’acuité visuelle, il y a netteté apparente si le diamètre de cette tache est inférieur ou égal à .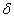
On note le point de l’axe le plus proche de l’objectif pour lequel ce critère de netteté apparente est satisfait.
a) Représenter sur la figure le point et son image , ainsi que les grandeurs .
b) Calculer la distance 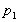du point à l’objectif en fonction de 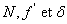. Commenter le résultat.
c) A.N.
Calculer 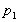pour 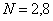, pour .
5) La tache centrale de diffraction donnée par une ouverture circulaire de diamètre a pour rayon angulaire . Quelle condition doit respecter le nombre d’ouverture de l’objectif de 50 mm de focale pour que la netteté ne soit pas limitée par la diffraction ?
Faire l’application numérique pour 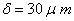et (on prendra 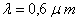). Conclusion ?

6) On s’intéresse dans cette question aux valeurs pouvant être données à certains paramètres.
a) Les nombres d’ouverture disponibles au niveau de l’objectif sont :
1,8 – 2,8 – 4 – 5,6 – 8 – 11 – 16 - 22
Quelle remarque peut-on faire et pourquoi ce choix ?
b) Les vitesses d’obturation disponibles, au niveau de l’appareil, sont, en secondes :
1/1000 – 1/500 – 1/250 – 1/60 – 1/30 – 1/15 – 1/8 – 1/4 – 1/2 - 1 – 2
Quelle remarque peut-on faire à propos de ce choix ?
c) Le photographe désire diminuer la profondeur de champ tout en conservant la même exposition à sa photographie. Comment doit-il opérer ?