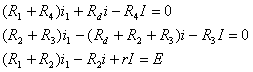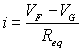Exercices d'électrocinétique des courants continus
|
1) Dans une résolution, il est important de bien poser les équations nécessaires.
Le nombre de branches est égal au nombre d'inconnues notées B, chaque branche apparaissant dans les équations par un courant électrique.
Ces équations seront fournies par les équations
de nœuds en nombre 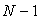 si le nombre de nœuds est N.
si le nombre de nœuds est N.
|

|
Le nombre d'équations de mailles nécessaires
sera 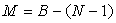 en faisant
attention dans le choix des mailles, qu'une maille ne soit pas la superposition
d'autres mailles.
en faisant
attention dans le choix des mailles, qu'une maille ne soit pas la superposition
d'autres mailles.
Les équations étant posées, il s'agit de résoudre
un système d'équations linéairement indépendantes
(système de Cramer).
Lorsque le nombre de branches est peu important, la résolution peut être
entreprise par substitution ; il est alors tout à fait efficace d'écrire
les équations de nœuds directement sur le schéma
Nous écrivons les équations pour les mailles ABD, CDB et EABC.
 ð
ð 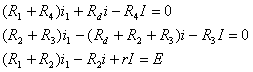
Une méthode de résolution simple consiste à procéder par substitution en gardant en dernier i puisque seul ce courant est demandé. Le lecteur vérifiera que l'on trouve le résultat du 2)3).
2)3)
|

|
Le théorème de Thévenin (ou de Norton) consiste à faire une coupure notée FG dans la branche BD et à remplacer par un générateur de tension équivalent (Thévenin) ou par un générateur de courant équivalent (Norton)
|
Calcul de la résistance équivalente 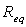
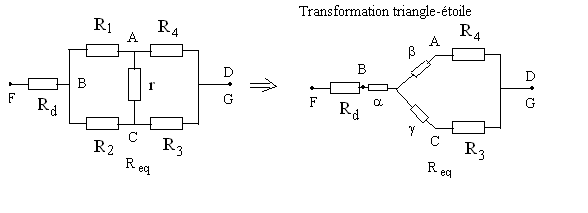
Dans la transformation triangle étoile représentée ci-dessus,
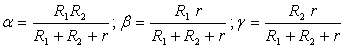

Calcul de la différence de potentiel 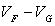
Le courant i dans la branche du galvanomètre
est égal à : 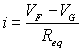
Ce courant est nul (relation d'équilibrage du pont de
Wheastone) pour 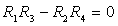
Remarque : cette dernière relation s'établit
beaucoup plus simplement en remarquant que pour 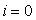 ,
la différence de potentiel
,
la différence de potentiel 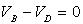
![]() si le nombre de nœuds est N.
si le nombre de nœuds est N.
 ð
ð