Exercices sur les milieux magnétiques
1)
|

|
Deux dipôles magnétiques de moments 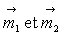 sont à distance fixe l’un de l’autre mais peuvent s’orienter librement
dans le plan.
sont à distance fixe l’un de l’autre mais peuvent s’orienter librement
dans le plan.
a) Calculer l’énergie potentielle du système
b) Rechercher les positions d’équilibre
stable
c) Calculer la force d’attraction entre les deux
dipôles occupant les positions d’équilibre stable
|
| Réponse
1a | Réponse
1b | Réponse
1c |
2) Un aimant permanent, en forme de cylindre de révolution
de hauteur 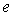 et
de rayon
et
de rayon 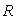 est
aimanté uniformément et parallèlement à son axe.
est
aimanté uniformément et parallèlement à son axe.
Calculer le champ magnétique  et l’excitation magnétique
et l’excitation magnétique  ,
créés en tout point
,
créés en tout point  intérieur ou extérieur de l’axe, en fonction du vecteur aimantation
intérieur ou extérieur de l’axe, en fonction du vecteur aimantation
 et des demi-angles
et des demi-angles
 des cônes
de sommet
des cônes
de sommet  s’appuyant
sur les bases du cylindre [
s’appuyant
sur les bases du cylindre [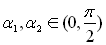 ].
Etudier les cas limites :
].
Etudier les cas limites :  (disque) et
(disque) et  (barreau)
pour
(barreau)
pour  intérieur
à l’aimant.
intérieur
à l’aimant.
| Réponse
2 |
3) Un barreau cylindrique, de rayon a, de très
grande longueur, est aimanté uniformément perpendiculairement
à son axe  .
Soit
.
Soit 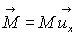 le vecteur
aimantation.
le vecteur
aimantation.
On se propose de calculer, en tout point intérieur et extérieur,
le potentiel-vecteur  et le champ magnétique
et le champ magnétique  .
.
On montrera que  ,
on déduira l’équation aux dérivées partielles
,
on déduira l’équation aux dérivées partielles  dont on vérifiera que la solution a pour forme générale
dont on vérifiera que la solution a pour forme générale
 .
.
On rappelle que : 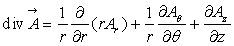
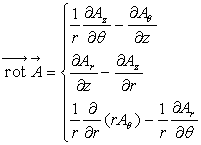
| Réponse
3 |
4) Une sphère homogène, de rayon a,
possède une aimantation uniforme 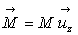 .
L’origine des coordonnées est choisie au centre de la sphère et
on utilise les coordonnées sphériques
.
L’origine des coordonnées est choisie au centre de la sphère et
on utilise les coordonnées sphériques  .
.
On se propose de calculer, en tout point intérieur et extérieur,
le potentiel-vecteur  et le champ magnétique
et le champ magnétique  .
.
On montrera que  ,
on déduira l’équation aux dérivées partielles
,
on déduira l’équation aux dérivées partielles  dont on vérifiera que la solution a pour forme générale
dont on vérifiera que la solution a pour forme générale
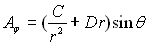 .
.
On rappelle que : 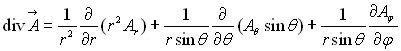
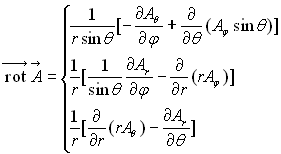
| Réponse
4 |
5) Electroaimant à pièces polaires tronconiques
|

|
On considère un électroaimant dont les
pièces polaires cylindriques se prolongent au niveau de l’entrefer
par des troncs de cône de révolution de même sommet
O et de demi-angle au sommet a .
Le rayon varie de 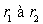 . .
On ne se préoccupera pas de la façon dont le circuit magnétique
se referme : les cylindres pourront être supposés infiniment
longs.
L’aimantation  est
supposée uniforme, y compris dans les parties tronconiques. est
supposée uniforme, y compris dans les parties tronconiques.
|
a) Calculer les courants d’aimantation équivalents
dans les parties cylindriques. En déduire le champ magnétique
 créé
en O par les parties cylindriques.
créé
en O par les parties cylindriques.
b) Calculer les courants d’aimantation équivalents dans les parties
tronconiques. En déduire le champ magnétique 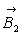 créé
en O que l’on exprimera en fonction de
créé
en O que l’on exprimera en fonction de 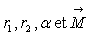 .
.
c) Pour  donnés,
montrer qu’il existe une valeur
donnés,
montrer qu’il existe une valeur  pour
laquelle
pour
laquelle  est maximal.
est maximal.
d) Pour 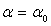 ,
calculer le champ magnétique total en O.
,
calculer le champ magnétique total en O.
A.N. 
Représenter l’allure des lignes de champ dans l’entrefer.
| Réponse
5a | Réponse
5b | Réponse
5c | Réponse
5d |
6) Aimants permanents
|

|
On considère un aimant permanent torique. La section
droite du tore a une aire S. L’entrefer est assimilable à
un " cylindre " de section droite d’aire s. On raisonnera
le long d’une circonférence moyenne et sur les champs moyens 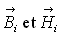 (dans
le matériau), (dans
le matériau), 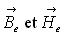 (dans
l’entrefer). Les modules de ces champs sont supposés constants. (dans
l’entrefer). Les modules de ces champs sont supposés constants.
|
Les longueurs de parcours dans le matériau et dans l’entrefer
sont respectivement L et l.
On néglige les parties tronconiques de l’aimant. On pose  rapport
des volumes de l’aimant et de l’entrefer.
rapport
des volumes de l’aimant et de l’entrefer.
a) La courbe de désaimantation du matériau est représentée
entre les valeurs  par
une fonction monotone décroissante
par
une fonction monotone décroissante  [voir
figure].
[voir
figure].
Le rapport u ayant une valeur fixée, comment choisir le " point
de fonctionnement " sur cette courbe pour que le champ dans l’entrefer
soit maximal ?
Donner une représentation graphique simple. Commenter le résultat.
b) La fonction f(H) peut approximativement être mise
sous la forme : 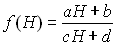 où
a, b, c, d sont des constantes.
où
a, b, c, d sont des constantes.
Vérifier que, dans ce cas, le point de fonctionnement se trouve sur la
diagonale du rectangle OADC.
A.N. 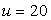 ;
champ rémanant
;
champ rémanant  ;
excitation coercitive
;
excitation coercitive 
Calculer la valeur maximale de  dans
l’entrefer ainsi que les rapports S/s et L/l.
dans
l’entrefer ainsi que les rapports S/s et L/l.
| Réponse
6a | Réponse
6b |
7) Etude microscopique de l’aimantation
- Rappeler les définitions de la susceptibilité
magnétique 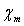 et
de la perméabilité magnétique relative
et
de la perméabilité magnétique relative  d’un
milieu magnétique linéaire, homogène et isotrope (l.h.i.)
d’un
milieu magnétique linéaire, homogène et isotrope (l.h.i.)
- Certains auteurs définissent la susceptibilité par la relation :

Etablir la relation entre  .
Quelle justification peut-on donner de la définition de
.
Quelle justification peut-on donner de la définition de  ?
Cas où
?
Cas où  .
.
1) Paramagnétisme
a) Donner une interprétation qualitative du paramagnétisme
au niveau microscopique dans le cas d’un système de moments magnétiques
localisés.
b) On considère un milieu constitué d’atomes dont le moment
cinétique se réduit à un spin simple 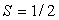 sans
moment cinétique orbital.
sans
moment cinétique orbital.
Dans ces conditions, chaque atome possède un moment magnétique :
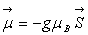 où
où  est
le magnéton de Bohr et g le facteur de décomposition spectrale
égal ici à 2.
est
le magnéton de Bohr et g le facteur de décomposition spectrale
égal ici à 2.
- Le milieu est placé dans un champ magnétique
uniforme 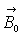 . Donner
les valeurs possibles de l’énergie d’interaction magnétique d’un
atome dans le champ magnétique.
. Donner
les valeurs possibles de l’énergie d’interaction magnétique d’un
atome dans le champ magnétique.
- La température du milieu est T . On néglige les interactions
entre les atomes (milieu dilué). Pour l’unité de volume contenant
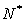 atomes, calculer
les populations atomiques correspondant à chaque état d’énergie.
atomes, calculer
les populations atomiques correspondant à chaque état d’énergie.
- Exprimer l’aimantation M(x) en fonction de  .
Donner l’allure de M(x). Interpréter cette courbe. Que
représente la grandeur
.
Donner l’allure de M(x). Interpréter cette courbe. Que
représente la grandeur  ?
?
- Pour  , calculer
la susceptibilité magnétique du milieu soit
, calculer
la susceptibilité magnétique du milieu soit 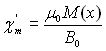 .
Vérifier que
.
Vérifier que 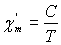 et
exprimer la constante de Curie C en fonction de
et
exprimer la constante de Curie C en fonction de 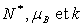 .
.
A.N. Calculer C relativement à 1 mole de substance
2) Ferromagnétisme
a) Rappeler brièvement l’interprétation
microscopique du ferromagnétisme.
b) Pour expliquer le comportement des corps ferromagnétiques on
suppose que chacun des atomes est soumis, outre à l’action du champ magnétique
appliqué 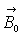 ,
à celle d’un champ moyen
,
à celle d’un champ moyen  (ou
" champ moléculaire " de Weiss) qui est censé traduire
l’action du milieu lui-même. Le champ
(ou
" champ moléculaire " de Weiss) qui est censé traduire
l’action du milieu lui-même. Le champ  est
supposé proportionnel à l’aimantation soit
est
supposé proportionnel à l’aimantation soit  où
a est une constante positive indépendante
de la température.
où
a est une constante positive indépendante
de la température.
- On suppose applicables les résultats obtenus en 7)1)
à condition de remplacer 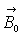 par
par
 . Montrer qu’en
l’absence de champ appliqué
. Montrer qu’en
l’absence de champ appliqué  ,
il peut exister une aimantation non nulle
,
il peut exister une aimantation non nulle 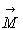 à
condition que la température T soit inférieure à
une température
à
condition que la température T soit inférieure à
une température  (température
de Curie) que l’on exprimera en fonction de
(température
de Curie) que l’on exprimera en fonction de 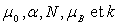 .
.
A.N. 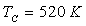
Calculer numériquement 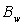 à
saturation en phase paramagnétique. Que conclure du résultat quant
à l’interaction entre atomes responsable du ferromagnétisme ?
à
saturation en phase paramagnétique. Que conclure du résultat quant
à l’interaction entre atomes responsable du ferromagnétisme ?
- Calculer en phase paramagnétique, loin de la saturation, la susceptibilité
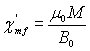 en fonction de
en fonction de
 .
.
- Calculer, en l’absence de champ appliqué et pour  mais
voisin de
mais
voisin de 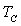 , le
rapport
, le
rapport  où
où
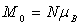 . Exprimer
. Exprimer  en
fonction de
en
fonction de 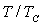 .
.
On rappelle que,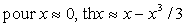
| Réponse
7 | Réponse
71a | Réponse
71b | Réponse
72a | Réponse
72b |

![]() sont à distance fixe l’un de l’autre mais peuvent s’orienter librement
dans le plan.
sont à distance fixe l’un de l’autre mais peuvent s’orienter librement
dans le plan.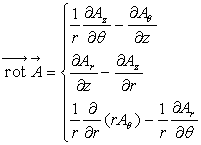
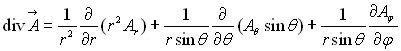
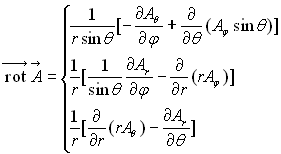



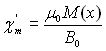 .
Vérifier que
.
Vérifier que 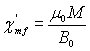 en fonction de
en fonction de