La matière en présence d'un champ électrique
Plan
1. Les milieux diélectriques
1.1. Les différents types de polarisation
1.2. Dipôle électrique
1.3. Potentiel électrique créé
par un diélectrique polarisé
1.4. Théorème de Gauss
1.5. Energie électrique
2. Les conducteurs
2.1. Le conducteur en équilibre électrostatique
2.2. Le conducteur en électrocinétique
Exercices
Annexe : La théorie des bandes d'énergie
(isolants, semi-conducteurs, conducteurs)
La matière soumise à un champ électrique réagit.
Nous distinguons deux types de matière :
- les diélectriques qui sont des isolants électriques,
c'est à dire des milieux dans lesquels il n'existe pas de charges
électriques libres et mobiles,
- les conducteurs qui sont des milieux pour lesquels il existe
des charges électriques libres et mobiles.
La création d’un champ électrique en une région
de l’espace est envisageable comme résultat de l’action de charges
électriques (voir loi de Coulomb). En fait, les champs électriques
permanents sont créés à partir de systèmes
appelés piles électriques dont l’étude relève
des cours de Thermochimie.
La frontière entre comportement diélectrique ou conducteur
n'est pas absolue, la matière pouvant être plus ou moins conductrice,
plus ou moins diélectrique. Les théories de la Physique classique,
qui sont abordées ici, s’avèrent très vite insuffisantes,
les théories quantiques et statistiques sont indispensables pour
expliquer les comportements isolants, semi-conducteurs et conducteurs de
la matière.
Le lecteur trouvera en annexe, à la fin du chapitre, des éléments
sur la théorie des bandes d’énergie.
1. Les milieux diélectriques
1.1. Les différents types de polarisation
1.1.1. Polarisation électronique des atomes et des ions
Sous l'action d'un champ électrique extérieur, les charges
positives et négatives se déplacent par rapport à
leurs positions d'équilibre, il y a distorsion de la fonction d’onde
électronique et création pour l’atome ou l’ion d’un dipôle.
Les couches électroniques des alcalins se déforment facilement
et leur polarisation électronique est élevée, à
l’inverse les gaz rares ont une faible polarisation.
La théorie dite de " l’électron élastiquement
lié " donne des résultats intéressants.
Les électrons d’un ion positif étant plus fortement liés
que ceux de l’atome de même nombre d’électrons, leur polarisation
électronique est plus faible ; c’est l’inverse qui se produit pour
un ion négatif.
1.1.2. Polarisation des molécules
Molécules non polaires
En l’absence de champ électrique extérieur, certaines molécules
ne possèdent pas de moment dipolaire et sont appelées non polaires.
Il suffit pour cela qu’elles possèdent un centre de symétrie :
c’est le cas des molécules diatomiques constituées d’atomes identiques,
des molécules linéaires telles que 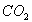 ,
à symétrie tétragonale comme
,
à symétrie tétragonale comme 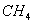 et
et 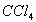 ou benzénique
comme
ou benzénique
comme 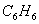 .
.
L’application d’un champ électrique extérieur provoque
:
- comme dans les atomes, une distorsion du nuage électronique
et une polarisation électronique,
- une modification de la position des noyaux à l’intérieur
de la molécule et une polarisation dite atomique.
La polarisation atomique est de l’ordre de 10% de la polarisation électronique.
Molécules polaires
Ces molécules possèdent un moment dipolaire permanent.
Le champ électrique extérieur, outre la polarisation
électronique et atomique, provoque une orientation, par interaction,
des dipôles dans la direction du champ. Cette polarisation est appelée
polarisation
d’orientation. Elle dépend très fortement de la température
comme le montre une théorie faisant intervenir le facteur de Boltzmann
et la fonction de Langevin.
1.1.3. Piézoélectricité. Pyroélectricité.
Ferroélectricité
On désigne par piézoélectricité la
propriété de certains cristaux de modifier (ou d’acquérir)
une polarisation sous l’effet d’efforts mécaniques, tels que compression
ou tractions.
Cette propriété trouve des applications sous forme d’allume-gaz
ou briquets piézoélectriques, de transducteurs dans les "
têtes de pick-up ", de générateurs ou de récepteurs
d’ultrasons, de " résonateurs " de faible amortissement, utilisés
pour produire des oscillations de fréquences très stables.
Seuls les cristaux qui ne possèdent pas de centre de symétrie
peuvent être piézoélectriques.
Parmi les 20 classes de cristaux piézoélectriques, 10
peuvent présenter une polarisation spontanée le long
d’un axe privilégié. C’est le phénomène de
pyroélectricité.
Parmi ces derniers, le sous-groupe des ferroélectriques
présente la particularité de garder une polarisation permanente,
c'est à dire d’avoir une polarisation qui ne cesse pas à
la suppression du champ extérieur. Cette propriété
de polarisation forte est utilisée dans les condensateurs de grande
capacité à faible encombrement.
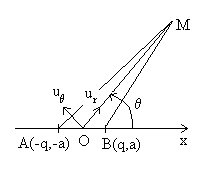
1.2. Dipôle électrique
On appelle dipôle électrique l’ensemble de deux charges
" voisines " 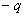 ,
,
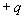 placées
en A et B. Le moment dipolaire est défini par le
vecteur
placées
en A et B. Le moment dipolaire est défini par le
vecteur 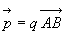
1.2.1. Potentiel et champ électriques créés
à grande distance
Ainsi, 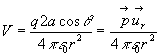
et 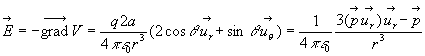
1.2.2. Action d’un champ électrique extérieur sur un
dipôle
Soit 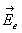 le champ
électrique extérieur. La charge positive q est située
en B de coordonnées (
le champ
électrique extérieur. La charge positive q est située
en B de coordonnées (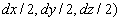 ,
la charge négative –q est en A de coordonnées (
,
la charge négative –q est en A de coordonnées (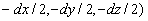 .
.
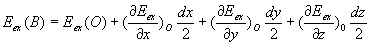
En remarquant que 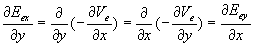 ,
on obtient
,
on obtient
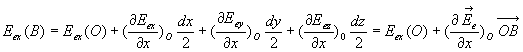
On trouve des relations identiques suivant les autres directions.
Système de forces s’exerçant sur le dipôle :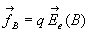 ;
; 
Résultante : 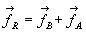 ð
ð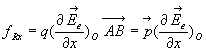
Compte tenu de relations identiques suivant les autres directions, 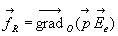
La résultante des forces s’exerçant sur un dipôle
est nulle dans un champ électrique extérieur uniforme.
L’énergie d’interaction d’un dipôle dans un champ électrique
extérieur est donc 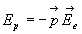
Moment résultant : 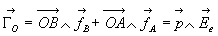
1.3. Potentiel électrique créé
par un diélectrique polarisé. Distribution équivalente
de charges.
On introduit le vecteur polarisation par la relation 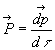 où
où 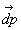 est le moment dipolaire de l'élément de volume
est le moment dipolaire de l'élément de volume 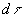 du
diélectrique de volume
du
diélectrique de volume 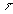 délimité par la surface fermée S.
délimité par la surface fermée S.
Soient A un point quelconque du diélectrique et M
un point extérieur au diélectrique.
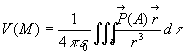 où
où 
Cette formule est d’un emploi simple si le vecteur polarisation est
uniforme, on retrouve alors le calcul de champs électrostatiques
pour une densité volumique de charge unité.
Dans le cas général, on remarque que 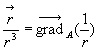 et
on utilise la relation d’analyse vectorielle
et
on utilise la relation d’analyse vectorielle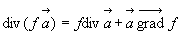
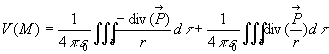
Soit, 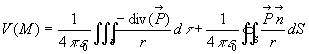 où
où 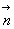 est le vecteur unitaire normal, en chaque point, à la surface fermée
S, orientée vers l’extérieur.
est le vecteur unitaire normal, en chaque point, à la surface fermée
S, orientée vers l’extérieur.
On constate que le potentiel créé par la polarisation est identique
à celui d’une distribution de charges de densité volumique 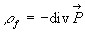 et de densité surfacique
et de densité surfacique 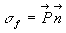 .
.
1.4. Théorème de Gauss
En dehors du diélectrique, le théorème de Gauss
est inchangé. Dans le diélectrique, il doit être réécrit
en introduisant la distribution équivalente de charges rendant compte
de la polarisation.
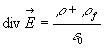 ð
ð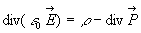
On obtient 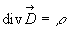 où
où 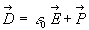 est appelée induction électrique.
est appelée induction électrique.
L'équation 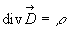 connue sous le nom d’équation de Maxwell-Gaussest l'une des quatre
équations de Maxwell.
connue sous le nom d’équation de Maxwell-Gaussest l'une des quatre
équations de Maxwell.
On conçoit que la polarisation est d'autant plus forte que le milieu
est dense et que le champ extérieur est fort.
Pour de nombreux matériaux et pour les champs électriques pas
trop intenses couramment utilisés, on peut écrire avec une bonne
approximation 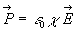 où
où 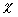 est appelée susceptibilité diélectrique du milieu
considéré.
est appelée susceptibilité diélectrique du milieu
considéré.
Ces diélectriques sont dits linéaires, homogènes, isotropes
(lhi). Sauf avis contraire, on se place dans cette hypothèse.
Alors 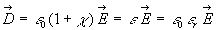 .
.
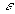 est la permittivité
diélectrique absolue et
est la permittivité
diélectrique absolue et 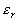 la permittivité diélectrique relative (par rapport au vide).
la permittivité diélectrique relative (par rapport au vide).
1.5. Energie électrique
L'énergie potentielle (d'origine électrique) d'une charge q
à potentiel V est 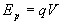 .
.
Pour une distribution volumique de charges de densité 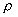 ,
le problème est plus complexe car la densité de charges et le
potentiel sont proportionnels (en effet
,
le problème est plus complexe car la densité de charges et le
potentiel sont proportionnels (en effet 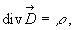
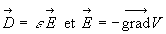 ð
ð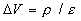 ,
soit
,
soit 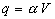 en appelant
q la charge de la distribution volumique à potentiel V).
en appelant
q la charge de la distribution volumique à potentiel V).
Soit une distribution volumique de charge q', de potentiel V'.
La charge varie de dq' , l'énergie potentielle varie de 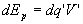 et le potentiel de
et le potentiel de  .
.
Aussi l'énergie potentielle d'une distribution de charges q à
potentiel V sera :
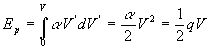
Pour une distribution volumique de densité 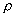 contenu
dans un volume
contenu
dans un volume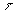 ,
on obtient ce résultat important
,
on obtient ce résultat important 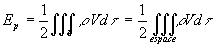 puisque
puisque 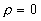 en
dehors du diélectrique
en
dehors du diélectrique
Cette relation peut être écrite : 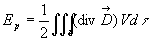 .
.
L'application de l'identité 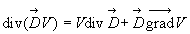 ,
le théorème d'Ostrogradsky et la relation
,
le théorème d'Ostrogradsky et la relation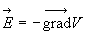 conduisent
à :
conduisent
à :
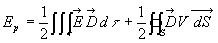 .
.
Si nous prenons la deuxième expression où l’intégration
est faite sur tout l’espace (c’est à dire à des distances infinies
du diélectrique), la dimension de S varie en 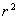 ,
l’intensité de
,
l’intensité de 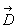 varie en
varie en  et
celle de V en
et
celle de V en 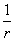 .
.
Ainsi 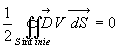 si
bien que
si
bien que 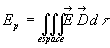
La densité volumique d'énergie électrique est égal
à : 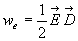 soit
soit 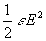 pour
un milieu linéaire, homogène, isotrope.
pour
un milieu linéaire, homogène, isotrope.
2. Les conducteurs
Il existe quatre types de conducteurs électriques :
-
les solides métalliques (les métaux dans la classification
de Mendeleïev) dans lesquels les atomes, en perdant 1, 2 ou 3 électrons
devenus libres qui forment une " mer d'électricité ", deviennent
des ions positifs. Les ions en interaction assurent la structure solide,
contrairement aux électrons ils ne sont pas " libres " de leurs
mouvements et ne peuvent que vibrer autour de leur position d'équilibre,
-
les liquides métalliques où les ions ont quelques possibilités
de déplacement,
-
les électrolytes où la molécule dans un solvant liquide
s'est séparé en deux ions de charges opposées pouvant
se déplacer dans le solvant,
-
les gaz ionisés (plasma) où l'atome a perdu 1, 2 ou 3 électrons.
Par simplification, les solides métalliques, qui seuls font l'objet
de ce cours, sont nommés conducteurs sans autre précision.
L'espace entre les conducteurs est occupé par des milieux non conducteurs
c'est à dire non susceptibles de mouvements de charges (vide, gaz
de molécules, diélectriques).
2.1. Le conducteur en équilibre électrostatique
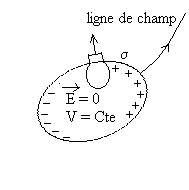 |
On place un conducteur dans une région
d'espace où règne un champ électrique.
Les charges libres (électrons de charges négatives) du
conducteur, sous l'effet du champ, se déplacent jusqu'à atteindre
des extrémités du conducteur, par défaut dans d'autres
extrémités il y aura des charges positives. Le déséquilibre
des charges va induire un champ électrique qui s'oppose au champ
électrique qui régnait en l'absence du conducteur.
Le mouvement des charges cessera (un équilibre électrostatique
s'établira) lorsque les deux champs s'opposeront en tout point intérieur
du conducteur. |
Le champ électrique, à l'équilibre électrostatique,
sera nul en tout point intérieur du conducteur.
Par application de  ,
on déduit que le potentiel est constant à l'intérieur
du conducteur.
,
on déduit que le potentiel est constant à l'intérieur
du conducteur.
Par application de 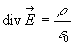 ,
on déduit que la densité volumique de charges est nulle. La distribution
de charges est surfacique et on appelle
,
on déduit que la densité volumique de charges est nulle. La distribution
de charges est surfacique et on appelle 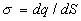 la densité superficielle de charges.
la densité superficielle de charges.
A l'extérieur immédiat du conducteur, le champ à
la direction de la normale à la surface, seules les charges infiniment
proches étant influantes.
L'application du théorème de Gauss sur la surface fermée
représentée conduit à : 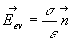 où
où 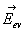 est
le champ électrostatique extérieur au voisinage du conducteur,
est
le champ électrostatique extérieur au voisinage du conducteur, 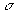 la densité superficielle de charges à l'endroit considéré,
la densité superficielle de charges à l'endroit considéré,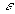 la permittivité diélectrique du milieu extérieur et
la permittivité diélectrique du milieu extérieur et 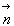 le vecteur unitaire normal orienté vers l'extérieur du conducteur.
le vecteur unitaire normal orienté vers l'extérieur du conducteur.
Sur la surface, le champ est égal à 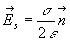 .
Il y a donc une discontinuité du champ à la traversée
de la surface chargée (ceci est vrai même si le matériau
n'est pas conducteur ð voir équations
de Maxwell).
.
Il y a donc une discontinuité du champ à la traversée
de la surface chargée (ceci est vrai même si le matériau
n'est pas conducteur ð voir équations
de Maxwell).
Par contre, il n'y a jamais de discontinuité de la fonction potentiel
V : ceci se démontre à partir du théorème
de Stokes et de la propriété 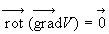 qui entraîne la continuité de la composante tangentielle du champ.
qui entraîne la continuité de la composante tangentielle du champ.
La charge Q répartie à la surface d'un conducteur se calcule
à partir de :
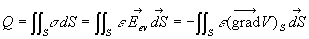 où S est la surface du conducteur.
où S est la surface du conducteur.
On remarquera la proportionnalité entre Q et V. Par suite 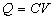 où C est la capacité du conducteur qui ne dépend
que de la forme du conducteur et de la permittivité du milieu extérieur.
La capacité C est positive puisque les lignes de champ (ligne
tangente en chaque point au champ) s'éloignent du conducteur lorsque
sa surface est chargé positivement.
où C est la capacité du conducteur qui ne dépend
que de la forme du conducteur et de la permittivité du milieu extérieur.
La capacité C est positive puisque les lignes de champ (ligne
tangente en chaque point au champ) s'éloignent du conducteur lorsque
sa surface est chargé positivement.
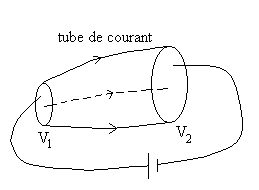
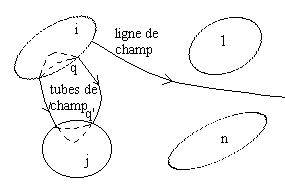
2.1.1. Ensemble de conducteurs en équilibre électrostatique
Il détermine sur les surfaces des conducteurs i et j, deux éléments
de surface appelés éléments correspondants. Ces éléments
correspondants sont porteurs de deux charges notées q et q'.
Le tube de courant et deux surfaces intérieures à chacun des conducteurs
i et j constituent une sur face fermée  .
L'application du théorème de Gauss donne
.
L'application du théorème de Gauss donne 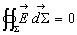 et donc
et donc 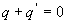 . Ceci
constitue le théorème des éléments correspondants,
on dit qu'il y a influence entre conducteurs.
. Ceci
constitue le théorème des éléments correspondants,
on dit qu'il y a influence entre conducteurs.
- Imaginons le cas où le conducteur i est au potentiel
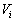 ,
les autres conducteurs étant à potentiels nuls.
,
les autres conducteurs étant à potentiels nuls.
Le conducteur i sera porteur d'une charge 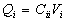 ,
les autres conducteurs, par influence, de charges
,
les autres conducteurs, par influence, de charges 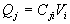 avec
avec 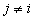 .
.
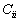 est appelée
la capacité du conducteur i en présence des autres conducteurs,
est appelée
la capacité du conducteur i en présence des autres conducteurs, 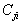 le coefficient d'influence du conducteur j du au conducteur i.
le coefficient d'influence du conducteur j du au conducteur i.
Nous remarquons que 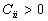 ,
que
,
que 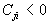 et que
et que 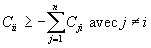 compte tenu de ce que nous avons dit sur le sens des lignes de champ et du fait
que certaines lignes de champ issues du conducteur i puissent ne pas rencontrer
de conducteurs.
compte tenu de ce que nous avons dit sur le sens des lignes de champ et du fait
que certaines lignes de champ issues du conducteur i puissent ne pas rencontrer
de conducteurs.
- Imaginons maintenant le cas où le conducteur j est au potentiel
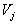 ,
les autres conducteurs étant à potentiels nuls.
,
les autres conducteurs étant à potentiels nuls.
le conducteur j sera porteur d'une charge  ,
les autres conducteurs, par influence, de charges
,
les autres conducteurs, par influence, de charges 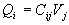 avec
avec 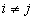 .
.
Si  , les lignes
de champ dans le deuxième cas sont identiques mais de sens opposé
au premier cas si bien que
, les lignes
de champ dans le deuxième cas sont identiques mais de sens opposé
au premier cas si bien que 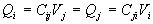 ð
ð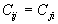 avec
avec 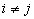 . Le
coefficient
. Le
coefficient 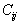 doit être appelé coefficient d'influence mutuelle.
doit être appelé coefficient d'influence mutuelle.
- Si nous imaginons maintenant le cas où les conducteurs sont à
potentiel
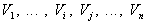 la
répartition des charges, compte tenu de la linéarité
des équations de l'électrostatique sera :
la
répartition des charges, compte tenu de la linéarité
des équations de l'électrostatique sera :
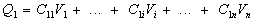 soit
soit 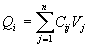
2.1.2. Energie
Pour " porter " une charge 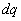 sur un conducteur à potentiel
sur un conducteur à potentiel 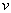 ,
l'opérateur extérieure doit fournir une énergie
,
l'opérateur extérieure doit fournir une énergie 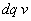 acquise
sous forme d'énergie potentielle électrique. Le potentiel électrique
varie de
acquise
sous forme d'énergie potentielle électrique. Le potentiel électrique
varie de 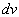 tel
que
tel
que 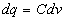 .
.
Pour un conducteur à potentiel V, l'énergie potentielle
électrostatique sera :
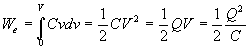
Pour n conducteurs 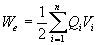
2.1.3. Condensateurs
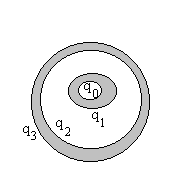
L'application du théorème de Gauss sur une surface fermée
intérieure au conducteur 1 conduit à 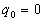 ce
qui veut dire que ce conducteur peut être plein ou creux.
ce
qui veut dire que ce conducteur peut être plein ou creux.
L'application du théorème de Gauss sur une surface fermée
intérieure au conducteur 2 conduit à 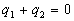 .
Nous posons
.
Nous posons  .
.
L'application du théorème de Gauss sur une surface fermée
entourant le conducteur 2 conduit à 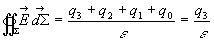 .
Vis à vis de l'extérieur, tout se passe comme si le conducteur
2 était plein.
.
Vis à vis de l'extérieur, tout se passe comme si le conducteur
2 était plein.
Soit le cas particulier 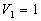 et
et 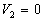 , le champ
à l'extérieur du conducteur 2 est nul ð
, le champ
à l'extérieur du conducteur 2 est nul ð .
Par suite,
.
Par suite, 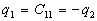 et
et 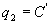 ce qui
démontre que
ce qui
démontre que 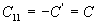 où C est appelée la capacité du condensateur.
où C est appelée la capacité du condensateur.
En remplaçant on obtient 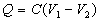 relation
du condensateur et
relation
du condensateur et 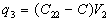
L'énergie s'obtient par application de la formule pour un ensemble de
conducteurs soit 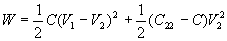 .
.
L'énergie du condensateur est 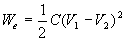 partie récupérable de l'énergie lorsque l'on décharge
le condensateur c'est à dire lorsque l'on porte les deux conducteurs
au même potentiel
partie récupérable de l'énergie lorsque l'on décharge
le condensateur c'est à dire lorsque l'on porte les deux conducteurs
au même potentiel  .
.
Dans la pratique on relie le conducteur extérieur à la " terre
" (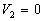 ) pour éviter
les décharges involontaires.
) pour éviter
les décharges involontaires.
Le calcul des capacités des condensateurs plan, cylindrique
à symétrie de révolution, sphérique à
symétrie sphérique, le calcul de la capacité d'un
conducteur sphérique constituent des exercices incontournables.
Formule générale de la capacité d'un condensateur
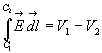 suivant une ligne
de champ
suivant une ligne
de champ
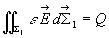 ð
ð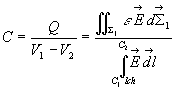
2.2. Le conducteur en électrocinétique
2.2.1. Loi d'Ohm
 |
Aux extrémités d'un conducteur,
on entretient par l'intermédiaire d'un générateur
une différence de potentiel continue.
Le champ électrique va provoquer le mouvement dans une direction
des charges libres (électrons). Le mouvement des électrons
est gêné par les chocs qu'ils subissent sur les ions fixes
du métal.
Avant la création du champ électrique, les électrons
avaient un mouvement du à l'agitation thermique. |
En moyenne, à un instant donné quelconque, leur vecteur
vitesse était nul.
Le principe fondamental de la dynamique pour un électron permet
d'écrire :
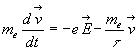 où le terme
où le terme 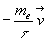 appelé
" force de relaxation " traduit la gène due aux chocs contre les ions
(nous l'avons supposé proportionnel au vecteur vitesse).
appelé
" force de relaxation " traduit la gène due aux chocs contre les ions
(nous l'avons supposé proportionnel au vecteur vitesse).
La solution de cette équation différentielle donne 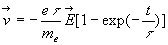 .
Nous avons considéré qu'à l'instant initial le vecteur
vitesse était nul (en fait, il s'agit d'un vecteur vitesse moyen pour
l'ensemble des électrons).
.
Nous avons considéré qu'à l'instant initial le vecteur
vitesse était nul (en fait, il s'agit d'un vecteur vitesse moyen pour
l'ensemble des électrons).
A partir d'un temps 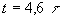 ,
la vitesse limite
,
la vitesse limite 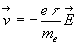 est atteinte à mieux que 1%.
est atteinte à mieux que 1%.
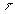 est la constante
de temps, elle caractérise le temps d’établissement du régime.
est la constante
de temps, elle caractérise le temps d’établissement du régime.
Une autre façon de raisonner considère que, juste après
un choc, en moyenne le vecteur vitesse est nul et que l'électron subit
la force électrique pendant la durée 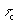 entre deux chocs.
entre deux chocs.
Il atteint, au moment du choc suivant, une vitesse 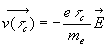 .
.
La vitesse moyenne de déplacement des électrons est égal
à 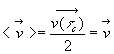
Ce deuxième raisonnement donne une interprétation physique intéressante
de 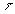 , liée
à la durée entre deux chocs donc au libre parcours moyen et à
la vitesse d’agitation thermique des électrons libres du métal.
, liée
à la durée entre deux chocs donc au libre parcours moyen et à
la vitesse d’agitation thermique des électrons libres du métal.
Cette interprétation nous permet d’admettre que le temps d'établissement
du régime est très faible, c'est à dire que la relation 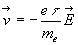 est vraie à chaque instant. Nous pouvons généraliser cette
relation à des champs variables où les temps caractéristiques
de variation (période par exemple) seraient très supérieures
à la constante de temps.
est vraie à chaque instant. Nous pouvons généraliser cette
relation à des champs variables où les temps caractéristiques
de variation (période par exemple) seraient très supérieures
à la constante de temps.
L'intensité du courant électrique est définie comme la
quantité d'électricité qui traverse par unité de
temps une section S du conducteur.
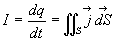 où
où 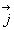 est le vecteur densité de courant.
est le vecteur densité de courant.
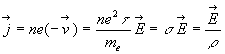 où n
est le nombre d'électrons libres par unité de volume du métal,
où n
est le nombre d'électrons libres par unité de volume du métal,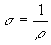 est
appelé la conductivité et l'inverse
est
appelé la conductivité et l'inverse 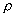 la
résistivité.
la
résistivité.
La relation 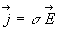 constitue l'expression locale de la très importante loi d'Ohm.
constitue l'expression locale de la très importante loi d'Ohm.
Remarques :
- l'habitude, héritée de l'histoire des Sciences, est de considérer
un mouvement de charges positives ; c’est pourquoi nous avons écrit
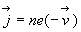 au lieu de
au lieu de 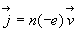
-
l’interprétation de la résistivité en termes de libre
parcours moyen et de vitesse d’agitation thermique ne conduit pas à
des résultats satisfaisants quant au variation de la résistivité
avec la température … ce qui prouve les limites de cette théorie
classique
-
" l’agitation thermique des électrons libres d’un métal "
n’augmente pas son énergie interne … seule une théorie quantique
permet des interprétations satisfaisantes
- on note une difficulté de notation communément admise :
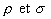 représentent parfois la densité volumique de charges et la densité
surfacique de charges, parfois la résistivité et la conductivité
d'un matériau conducteur.
représentent parfois la densité volumique de charges et la densité
surfacique de charges, parfois la résistivité et la conductivité
d'un matériau conducteur.
Expression intégrale de la loi d'Ohm
Soit un conducteur délimité par deux surfaces équipotentielles 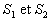 à potentiel
à potentiel 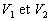 .
.
On appelle ligne de courant le " trajet " suivi par les charges.
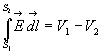 suivant une ligne
de courant,
suivant une ligne
de courant, 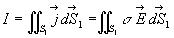
ð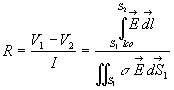
R est appelée résistance électrique
Cette relation constitue l'expression intégrale de la très
importante loi d'Ohm.
Remarque
Il y a ressemblance des formules entre la capacité d'un condensateur
et la résistance d'un conducteur. L'analogie est plus complète
si on remarque, qu'en électrostatique pour un diélectrique et
en électrocinétique pour un conducteur, la fonction potentiel
obéit à 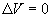 .
.
Nous admettons (ce qui semble évident pour un mouvement continu
de charges mobiles et sera montré dans le chapitre sur les équations
de Maxwell chaque fois que la loi d'Ohm est applicable) que la densité
volumique de l'ensemble de toutes les charges d'un conducteur est nulle.
Pour un diélectrique et un conducteur de même forme, les équipotentielles
donc les lignes de champ et les lignes de courant sont identiques et 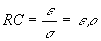
2.2.2. Energie (effet Joule)
Considérons un électron sur une ligne de courant, son
sens est celui des potentiels croissants puisque sa charge est négative.
Sa variation d'énergie potentielle électrique lorsqu'il
passe d'un point M en un point M' infiniment voisin est égale
à :
 puisque
puisque 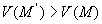
L'électron a perdu de l'énergie électrique, elle
n'est pas devenue cinétique puisque le vecteur vitesse est constant
sauf à l'établissement du régime.
Cette énergie est devenue de l'énergie interne lors des
chocs sur les ions (augmentation de leur agitation thermique, donc de la
température qui peut se stabiliser si le conducteur échange
de la chaleur avec l'extérieur).
Le nombre d'électron à vitesse 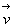 traversant un élément de surface
traversant un élément de surface 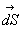 par unité de temps est égal à
par unité de temps est égal à 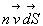 .
.
La perte d'énergie électrique est 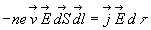 (le signe – introduit est conventionnel : il compte positivement la perte
d’énergie électrique, c’est à dire le gain d’énergie
d’une autre forme).
(le signe – introduit est conventionnel : il compte positivement la perte
d’énergie électrique, c’est à dire le gain d’énergie
d’une autre forme).
Ce phénomène est connu sous le nom d'effet Joule.
L'expression locale de la puissance volumique dissipée par effet joule
s'écrit donc 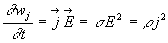 .
.
L'expression intégrale pour le conducteur conduit à une puissance 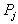 dissipée par effet Joule égale à
dissipée par effet Joule égale à 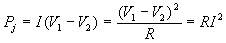
2.2.3. Validité de la loi d'Ohm à hautes fréquences
La mesure de la conductivité permet de connaître la valeur de
la constante de temps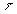 ,
compte tenu du modèle proposé. Ainsi pour le cuivre de masse molaire
égale à 63,6 g, de masse volumique
,
compte tenu du modèle proposé. Ainsi pour le cuivre de masse molaire
égale à 63,6 g, de masse volumique 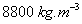 ,
de conductivité égale à
,
de conductivité égale à 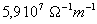 ,
qui dans la liaison métallique libère un électron par atome,
on trouve
,
qui dans la liaison métallique libère un électron par atome,
on trouve 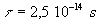 .
.
On conçoit alors que la loi d’Ohm soit valable jusqu'à des fréquences
atteignant 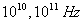 ce que l’on écrit sous la forme
ce que l’on écrit sous la forme 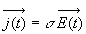 ou
ou 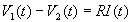
La vitesse des électrons est intéressante à connaître
: elle est pour un conducteur en cuivre de 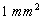 de
section, parcouru pat un courant de 1 A, de
de
section, parcouru pat un courant de 1 A, de 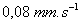 .
.
Exercices
Diélectrique
En coordonnées sphériques avec symétrie de révolution
autour d’un axe, 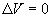 s’écrit :
s’écrit :
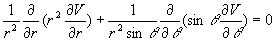
1) Montrer en cherchant pour 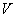 des solutions sous la forme
des solutions sous la forme 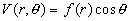 que
que 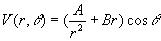
2) Appliquer cette démarche :
- au cas d’une sphère de rayon a, constituée d’un
matériau di électrique de permittivité
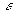 ,
placée dans le vide où régnait un champ électrique
uniforme
,
placée dans le vide où régnait un champ électrique
uniforme 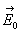 ,
,
- au cas d’un diélectrique infini de permittivité
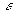 où régnait un champ uniforme
où régnait un champ uniforme 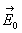 et dans lequel on a creusé une sphère de rayon a
et dans lequel on a creusé une sphère de rayon a
Annexe : Théorie des bandes d’énergie
(isolants, semi-conducteurs et conducteurs)
En mécanique quantique (le lecteur pourra se contenter de généraliser
le calcul préquantique de " l’atome de Bohr "), on apprend que les énergies
possibles, pour tout système, forment un spectre discret et qu’à
un niveau d’énergie possible 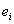 ,
il correspond plusieurs états quantiques (sous-états correspondant
à une même énergie appelés dégénérescence,
la variable
,
il correspond plusieurs états quantiques (sous-états correspondant
à une même énergie appelés dégénérescence,
la variable 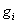 traduit le nombre de dégénérescence).
traduit le nombre de dégénérescence).
Ces propos sont applicables aux électrons d’un atome (voir cours
d’atomistique) en y ajoutant le Principe d’exclusion de Pauli à
savoir il ne peut y avoir plus d’un électron par sous-état
quantique.
Imaginons une chaîne de N atomes identiques initialement
éloignées les uns des autres : ils vont, lors de la constitution
du cristal, interagir entre eux ce qui va entraîner une modification
des niveaux d’énergie pour les électrons. Ceci est une conséquence
du Principe d’exclusion de Pauli, chaque niveau d’énergie va se
scinder en N niveaux discrets afin que ne corresponde pas la même
énergie à deux mêmes sous-états quantiques.
Ainsi, autour d’un niveau d’énergie initiale, se forment N
niveaux d’énergie voisins. Ces niveaux d’énergie sont, souvent,
si proches les uns des autres que l’on pourra parler de continuum d’énergie
(spectre continu d’énergie) autour de l’énergie initiale
c’est à dire dans un intervalle (bande) d’énergie.
Les électrons ne peuvent avoir accès aux niveaux d’énergie
entre les bandes. On dit que les niveaux d’énergie dans les bandes
sont permis ou possibles tandis que les niveaux d’énergie
entre les bandes ne sont pas permis ou interdits.
Le lecteur qui aurait quelques difficultés avec la " multiplication
" des niveaux d ‘énergie autour d’un niveau d’énergie fera
une similitude avec les systèmes couplés : le couplage de
deux systèmes de même fréquence de résonance
crée deux fréquences de résonance (fréquences
propres) situées de part et d’autre de la fréquence de résonance
initiale, le couplage de trois systèmes …
En Physique statistique, on apprend que le nombre 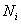 de particules (ici électrons), par niveau d’énergie
de particules (ici électrons), par niveau d’énergie 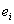 ,
est égal à
,
est égal à 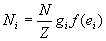 où
où  est la fonction de partition et
est la fonction de partition et 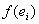 la probabilité pour une particule d’occuper un état quantique
de niveau d’énergie
la probabilité pour une particule d’occuper un état quantique
de niveau d’énergie 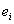 .
.
Dans le cas d’un continuum d’énergie, on écrira 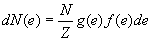 avec
avec 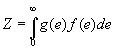 ,
, 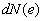 est le nombre de particules dans l’intervalle d’énergie
est le nombre de particules dans l’intervalle d’énergie 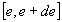 .
.
Les électrons obéissent à la statistique de Fermi-Dirac
et 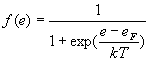 où
où  est le niveau d’énergie de Fermi.
est le niveau d’énergie de Fermi.
Comportement isolant, semi-conducteur, conducteur d’un
matériau
Au zéro absolu
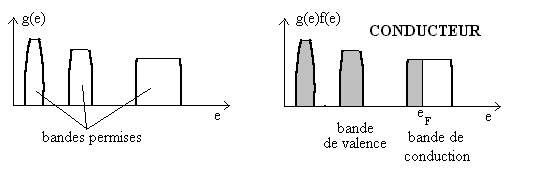
L’étude de la fonction 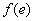 montrent que les bandes permissent se remplissent à partir des énergies
les plus faibles, celles dont l’interaction avec les noyaux sont les plus fortes.
montrent que les bandes permissent se remplissent à partir des énergies
les plus faibles, celles dont l’interaction avec les noyaux sont les plus fortes.
Toutes les bandes permises qui ont des énergies inférieures
à celles de Fermi sont entièrement remplies par les électrons
(on appelle bande de valence, la bande pleine dont les énergies
sont les plus élevées parce qu’elle contient des électrons
des couches externes des atomes dits électrons de valence). Pour
des énergies supérieures à celles de Fermi, il n’y
a pas d’occupation par des électrons. Si le niveau d’énergie
de Fermi est dans une bande, celle-ci, incomplètement remplie (ou
pas totalement vide) est une bande de conduction.
L’application d’un champ électrique ne permet pas (pas assez
d’énergie) à un électron de changer de bande d’énergie
et, par exemple de passer d’une bande entièrement pleine à
une bande totalement vide. Par contre, à l’intérieur d’une
bande, l’électron peut changer de niveau d’énergie.
Une bande pleine (de valence) ne peut être l’objet d’un courant
électrique puisque l’électron qui changerait de niveau ne
pourrait que déloger un autre électron qui viendrait à
sa place.
Par contre dans une bande non pleine (bande de conduction), un électron
peut se déplacer sur un niveau d’énergie non occupé.
Imaginons une bande de conduction où il y ait une seule place libre,
la Nième par ordre croissant d’énergie.
Les N-1 électrons peuvent se déplacer en utilisant cette
énergie libre et la courant électrique créés sera 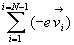 si
si  est la vitesse.
est la vitesse.
S’il y avait un Nième électron,
le courant serait nul, soit 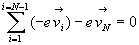 que l’on peut écrire
que l’on peut écrire 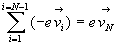 :
:
la conduction électrique résultant des mouvements des
N-1
électrons est équivalente à celle d’une particule,
appelée trou, de charge +e, de vitesse égale
à celle de l’électron manquant.

Si 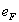 est situé
entre deux bandes permises, les bandes d’énergie sont entièrement
occupées ou vides, il ne peut y avoir de courant électrique.
est situé
entre deux bandes permises, les bandes d’énergie sont entièrement
occupées ou vides, il ne peut y avoir de courant électrique.
A une température absolue non nulle
Par rapport au zéro absolu, la différence de comportement
provient essentiellement de la modification de f(e) avec la température.
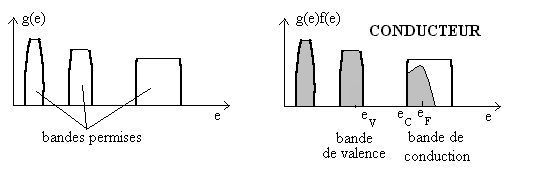
Le comportement conducteur ne change pas par rapport à ce qui se passe
à 
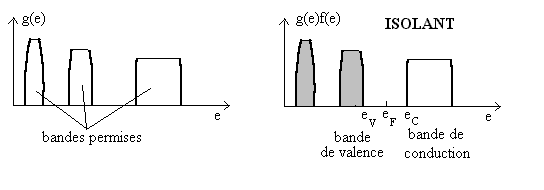
Si l’écart 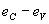 , appelé gap d’énergie, différence entre l’énergie
la plus faible de la bande de conduction et l’énergie la plus forte de
la bande de valence, est suffisamment important (5 eV), aucun électron
de la bande de valence ne peut, par énergie thermique, passer dans la bande
de conduction (initialement vide) et le matériau reste isolant.
, appelé gap d’énergie, différence entre l’énergie
la plus faible de la bande de conduction et l’énergie la plus forte de
la bande de valence, est suffisamment important (5 eV), aucun électron
de la bande de valence ne peut, par énergie thermique, passer dans la bande
de conduction (initialement vide) et le matériau reste isolant.
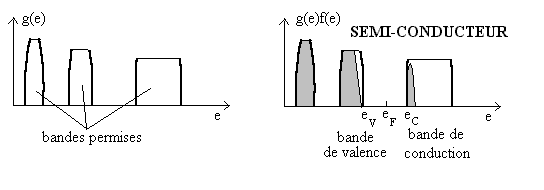
Si l’écart 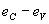 est de l’ordre de 1 eV, quelques (peu) électrons de la bande de
valence, par énergie thermique, passent dans la bande de conduction (initialement
vide). Sous l’effet d’un champ électrique, un courant se produit résultat
des mouvements des quelques électrons venus dans la bande de conduction
et, par défaut, d’un nombre égal de trous qui se sont produits,
dans la bande de valence, suite au départ d’électrons. Le nombre
de charges en mouvement reste faible et le matériau est dit semi-conducteur.
est de l’ordre de 1 eV, quelques (peu) électrons de la bande de
valence, par énergie thermique, passent dans la bande de conduction (initialement
vide). Sous l’effet d’un champ électrique, un courant se produit résultat
des mouvements des quelques électrons venus dans la bande de conduction
et, par défaut, d’un nombre égal de trous qui se sont produits,
dans la bande de valence, suite au départ d’électrons. Le nombre
de charges en mouvement reste faible et le matériau est dit semi-conducteur.
Parmi les matériaux semi-conducteurs, on trouve les minéraux
:
- Silicium ou Germanium (colonne IV de la classification de Mendeleïev
- des composés des colonnes III-V tels que arséniure
de gallium (GaAs)
- des composés ternaires des colonnes II-VI
On trouve aussi des semi-conducteurs organiques tels que l’anthracène
(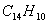 ), le naphtalène
(
), le naphtalène
(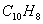 ) , le coronène
(
) , le coronène
( ), les cristaux
liquides utilisés comme afficheurs qui sont des mol écules à
noyaux benzéniques et des matériaux amorphes tels les verres.
), les cristaux
liquides utilisés comme afficheurs qui sont des mol écules à
noyaux benzéniques et des matériaux amorphes tels les verres.
Il est possible d’augmenter le nombre d’électrons de la bande
de conduction par dopage de type n (introduction d’impuretés d’un
élément pentavalent tel que phosphore (P), arsenic
(As) ou antimoine (Sb) ou d’augmenter le nombre de trous
de la bande de valence par dopage de type p (introduction d’impuretés
d’un élément trivalent tel que le bore (B), le gallium
(Ga) ou l’aluminium (Al).
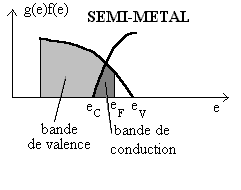
| Dans ce cas, le gap est inférieur à
1 eV, et il peut y avoir un léger recouvrement entre la bande
de valence et la bande de conduction si bien qu’il existe quelques trous
dans la bande de valence et quelques électrons dans la bande de
conduction. Le niveau de Fermi (commun aux deux bandes) étant dans
la zone de conduction, comme dans un métal, on parle de semi-métal.
On peut citer bismuth, l’arsenic, l’antimoine ou l’étain. |
 |
Problème
1) Pour un électron d'un cristal, la probabilité 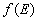 d’occupation d'un niveau d'énergie
d’occupation d'un niveau d'énergie 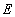 est donnée par :
est donnée par : 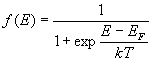 où
où 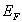 ,
potentiel chimique, est appelé niveau de Fermi.
,
potentiel chimique, est appelé niveau de Fermi.
Etudier cette fonction pour différentes valeurs de 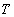 à partir de
à partir de 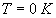 (on pourra poser
(on pourra poser 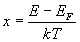 ).
Conclusion sur la façon de remplir les différents niveaux d'énergie.
).
Conclusion sur la façon de remplir les différents niveaux d'énergie.
2) Pour un semi-conducteur la concentration (nombre par unité
de volume) en électrons dans la bande de conduction est donnée
par : 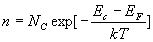 où
où 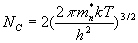 ,
celle en trous est donnée par :
,
celle en trous est donnée par : 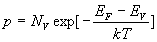 où
où 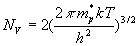
2)a)Que représentent 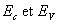 ?
?
2)b) Pour le fonctionnement intrinsèque d'un semi-conducteur,
la neutralité électrique impose  ,
en déduire la valeur de
,
en déduire la valeur de  ainsi que celle de
ainsi que celle de 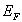 en fonction des données.
en fonction des données.
AN : Pour le Silicium, 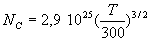 ;
; 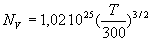 ,
, 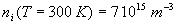 ;
calculer
;
calculer 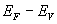 et
et 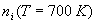 .
Montrer que
.
Montrer que 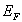 varie peu avec la température.
varie peu avec la température.
3) Dans une situation plus générale, le semi-conducteur
dopé contient à la fois des atomes donneurs et accepteurs en concentrations
respectives 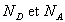 .
.
A une température quelconque, seule une fraction de ces atomes est ionisée,
soient 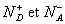 les
concentrations des ions ainsi formés
les
concentrations des ions ainsi formés
3)a) Ecrire l’équation de neutralité électrique
et montrer que 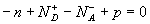 .
.
3)b) Dans le cas où tous les atomes d’impuretés sont ionisés,
calculer 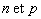 dans
le cas d’un dopage de type n ou d’un dosage de type p (pour les
dosages usuels, on envisagera
dans
le cas d’un dopage de type n ou d’un dosage de type p (pour les
dosages usuels, on envisagera 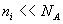 et
et 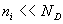 ).
).
4) Un semi-conducteur est dopé à l'aide d'atomes donneurs
en concentration 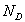 .
A la température
.
A la température 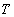 ,
supposée constante et de l'ordre de l'ambiante, on a
,
supposée constante et de l'ordre de l'ambiante, on a 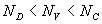 .
La densité d'atomes donneurs non ionisés vaut :
.
La densité d'atomes donneurs non ionisés vaut :  (
(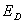 est l'énergie
du niveau donneur ;
est l'énergie
du niveau donneur ; 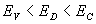 ).
).
4)a) Déterminer l'expression de la concentration  d'atomes donneurs ionisés
d'atomes donneurs ionisés
4)b) On étudie le comportement de 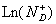 en fonction de
en fonction de  ,
lorsque le niveau de Fermi se déplace dans la bande interdite. Examiner
les deux cas limites pour lesquels
,
lorsque le niveau de Fermi se déplace dans la bande interdite. Examiner
les deux cas limites pour lesquels 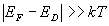 .
.
4)c) Représenter sur un même graphique, en fonction de 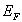 :
: 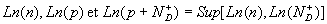
Commenter les différentes situations que l'on peut rencontrer.
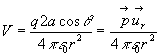
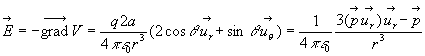
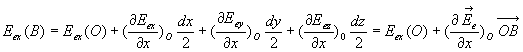
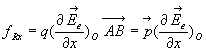
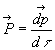 où
où 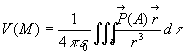 où
où 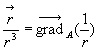 et
on utilise la relation d’analyse vectorielle
et
on utilise la relation d’analyse vectorielle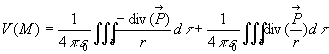
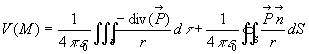 où
où 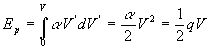
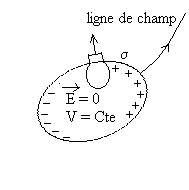
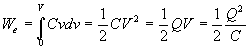
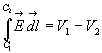 suivant une ligne
de champ
suivant une ligne
de champ 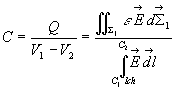

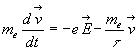 où le terme
où le terme 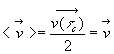
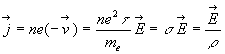 où n
est le nombre d'électrons libres par unité de volume du métal,
où n
est le nombre d'électrons libres par unité de volume du métal,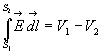 suivant une ligne
de courant,
suivant une ligne
de courant, 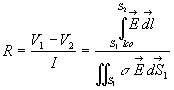
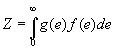 ,
, 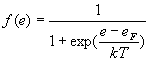 où
où 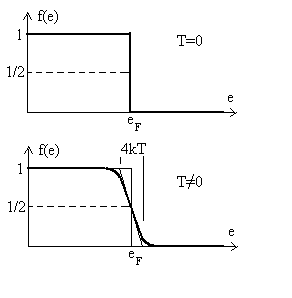






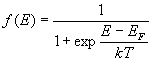 où
où  (
(