1)a) Le moment d'inertie d'un solide par rapport à un axe D est défini par :
où d représente la distance de l'élément de masse élémentaire dm à l'axe D.
Pour l'axe Oy,

1)b)

1)c)

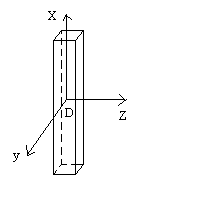Soit D le centre d'inertie de la tige.

1)d)
On utilise le théorème d'Huygens :
Le moment d'inertie par rapport à un axe est égal au moment d'inertie par rapport à un axe parallèle passant par le centre d'inertie du solide augmenté de la quantité où M est la masse du solide et d la distance entre les deux axes.

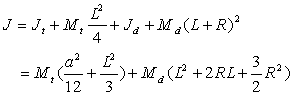
1)e)

2)a)

• Les forces de pesanteur
• Les liaisons au niveau de l'axe de rotation
• La poussée d'Archimède
• Les forces de frottement de l'air (viscosité)

Il est légitime de négliger dans la poussée d'Archimède puisque :

S'il n'existe aucune perte d'énergie mécanique (liaison parfaite au niveau de l'axe, pas de frottements d'air),
Ainsi, toute variation d'énergie cinétique est accompagnée d'une variation opposée d'énergie potentielle ð mouvement périodique.

2)b)

1^ère méthode : conservation de l'énergie mécanique

: énergie cinétique de rotation autour d'un axe fixe

Ainsi,

2^ème méthode : théorème du moment dynamique pour un mouvement de rotation autour d'un axe fixe

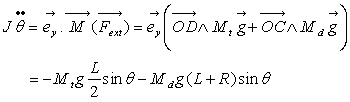
(équation différentielle du mouvement)

On multiplie cette dernière relation par et on intègre pour obtenir :

Le calcul de la constante se fait à partir des conditions initiales, et .

2)c)

Toutes les valeurs de q sont possibles (le pendule fait un tour complet) si

Si , alors avec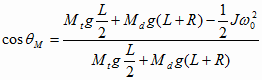

se calcule à partir de la relation

2)d) Pour calculer , on applique le théorème de la résultante dynamique :

relation que l'on peut expliciter à partir de l'équation différentielle du mouvement et de l'équation de conservation de l'énergie.

2)e) On linéarise l'équation différentielle du mouvement en écrivant que .

On obtient , soit si

En intégrant,

et ð

La période du mouvement est donnée par :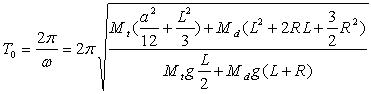

2)f)

L'équation peut être écrite sous la forme ð

On intègre cette dernière équation différentielle sur un quart de période l'angle évoluant de .

ð ð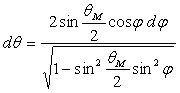

En remplaçant, on obtient : en faisant un développement limité justifié par la condition de l’ordre de quelques degrés.

Cette dernière intégrale ne présente pas de difficulté particulière et conduit à :
qui montre l'influence de l'amplitude de l'oscillation sur la période du pendule.

2)g)

si

ð

2)h)

Il y a amortissement des oscillations, c'est à dire perte d'énergie mécanique : Il faudra fournir ("remonter l'horloge") l'énergie mécanique perdue de temps en temps pour que l'horloge fonctionne en permanence.

3)a)

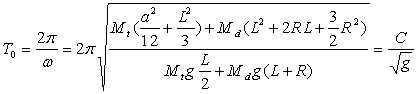
3)b) Le référentiel de l'avion (translation par rapport au référentiel lié au sol) en accélération n'est pas galiléen, il convient d'ajouter, pour étudier le mouvement du pendule dans le référentiel de l'avion, les forces d'inertie.
Le mouvement du pendule ne sera pas affecté si la réaction d'axe compense cette force d'inertie : le plan d'oscillation du pendule devra être perpendiculaire à la direction de l'avion.

3)c) Pour un pendule donné, les grandeurs physiques qui font varier la période d'oscillation, sont celles qui font varier l'intensité du champ de pesanteur, soient l'altitude et la latitude.
Si on admet que Singapour et Paris sont à la même altitude, la période sera affectée par le changement de latitude.

3)d)1)

En reportant

;
Compte tenu de la valeur de ces deux termes,

3)d)2)
;

3)d)3)

Le modèle est très satisfaisant, les différences (faibles) sont dues au fait que l'on a considéré que la Terre est sphérique alors qu'elle est légèrement aplatie aux deux pôles.

3)d)4)
L'horloge réglée à Paris ne l'est pas à Singapour.

3)e)
L'horloge à balancier ne fonctionne plus, celle à quartz n'est pas affectée par l'intensité de pesanteur.
Sur la Lune, l'intensité de pesanteur est six fois plus faible que sur la Terre. La période sur la Lune pour l'horloge à balancier sera fois plus grande que sur la Terre.