Etude d’un pendule composé

Etude d’un pendule composé

L’étude des mouvements dans un référentiel lié à la Terre sera conduite en négligeant les forces d’inertie de Coriolis : cela revient à " faire comme si " ce référentiel était galiléen, en remplaçant toutefois les forces de gravitation par les forces de pesanteur.

Le pendule est un balancier d’une horloge de campagne constitué d’une tige et d’un disque fixé à son extrémité inférieure.
L'ensemble du balancier forme un solide homogène en acier de masse volumique .
La tige, de forme parallélépipédique, a pour longueur , largeur et épaisseur .
Le disque est un cylindre de révolution de rayon , limité par deux sections droites distantes de .
L’axe du cylindre est parallèle à Oy, axe de rotation du pendule, perpendiculaire au plan de figure.

A l’instant choisi comme origine des temps, le pendule est en animé d’une vitesse angulaire .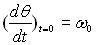
L’accélération de la pesanteur vaut localement , étant le vecteur unitaire de l’axe Oz.

1) Calcul du moment d’inertie
1)a) Définissez le moment d’inertie d’un solide par rapport à l’axe Oy.
1)b) Calculez le moment d’inertie du disque par rapport à son axe de révolution.
1)c) Calculez le moment d’inertie de la tige par rapport à un axe parallèle à Oy et passant par son centre d’inertie.
1)d) Calculez le moment d’inertie J du pendule par rapport à l’axe de rotation Oy ; quel théorème est-il judicieux d’employer ? Enoncez-le.
1)e) Application numérique : calculez J.

2) Etude du mouvement du pendule
2)a) Quelles sont les forces appliquées au pendule ? Est-il légitime de négliger la poussée d’Archimède ? Justifiez votre réponse.
Montrez par des considérations énergétiques que le mouvement est périodique si la liaison avec l’axe de rotation est parfaite et si on peut négliger les frottements dans l’air.

On suppose ces conditions remplies dans la suite du problème.

2)b) Etablissez, par deux méthodes différentes une relation liant à chaque instant ?
2)c) Déterminez le domaine de variation de suivant les valeurs de (on précisera la valeur de qui permet au pendule de faire un tour complet).
2)d) Déterminez la résultante des actions exercées par l’axe Oy sur le pendule.
2)e) On suppose que où est de l’ordre de quelques degrés.
Quelle propriété apparaît dans ce cas ? Quelle est alors la solution générale de l’équation différentielle ? Donnez la valeur littérale 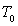de la période correspondante.
2)f) Pratiquement, l’angle a une valeur plus importante.
Montrez que la période du mouvement peut s’écrire :

Calculez T en fonction de 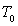et (on posera et on fera un développement qu’on limitera au deuxième ordre en ).
2)g) Calculez numériquement la période à Paris (). Quel est l’angle maximal 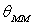tolérable si on veut que la période T diffère de moins de 1% de la période ?
2)h) L’étude a été faite en négligeant les forces de frottement dans l’air. En réalité ceux-ci existent et on suppose que le moment de ces forces par rapport à l’axe de rotation Oy peut s’écrire où est une constante positive et le vecteur unitaire de l’axe de rotation. La liaison avec l’axe de rotation est toujours supposée parfaite.
Ecrivez l’équation différentielle du mouvement du pendule dans le cas des oscillations de faible amplitude.
Donnez la solution générale en supposant que l’influence des frottements reste faible. Précisez l’allure de la courbe représentant les variations de l’élongation en fonction du temps.
Quelle conclusion tirez-vous concernant le mécanisme d’une horloge si le pendule est le balancier d’une horloge ?

3) Influence de la pesanteur sur le fonctionnement des horloges à balancier
Le pendule est le balancier d’une horloge, on néglige tout frottement et les oscillations ont faibles si bien que la période est .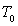
3)a) Comment varie la période avec l’intensité de pesanteur g ?
3)b) L’horloge est placée dans un avion, à Paris, sous la responsabilité d’un steward.
Au moment du décollage, l’appareil roulant sur une piste horizontale, l’accélération de l’avion peut être considérée comme constante. Le steward vous interroge : " Comment placer le plan d’oscillation du balancier pour que, ni la position d’équilibre, ni la période ne soient modifiées pendant le décollage ? "
Donnez votre réponse et justifiez-la.
3)c) L’avion atterrit à Singapour, lieu dont la latitude est , celle de Paris étant .
Quelles sont les grandeurs physiques susceptibles de faire varier la période 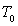lorsque l’horloge change de lieu ?
3)d) On veut préciser l’influence de la seule latitude (l’altitude restant nulle).
On considère que la Terre tourne à vitesse constante autour de l’axe des pôles ; on assimile le champ de gravitation total au seul champ créé par la Terre supposée formée d’une répartition de masses à symétrie sphérique.
On rappelle que l’accélération de la pesanteur est telle que le poids 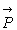d’un corps de masse m a pour expression .
3)d)1) Donnez l’expression vectorielle de en fonction du rayon de la Terre, de la latitude , de la période de rotation propre de la Terre et de l’expression où est la constante d’attraction universelle et la masse de la Terre. Que représente ?
3)d)2) Dans ce modèle, calculez les valeurs numériques de et de , intensités de l’accélération de pesanteur à Singapour et à Paris.
3)d)3) En fait, les mesures effectuées donnent : et . Comment justifier l’écart entre les valeurs mesurées et celles calculées en 3)d)2) ?
3)d)4) En ne tenant compte que de l’influence de la latitude, indiquez si l'horloge réglée à Paris est correctement réglée à Singapour. Précisez si elle avance ou retarde et calculez l’écart relatif de période ; est la période à Paris, celle à Singapour.
3)e) Au cours d’un voyage Terre-Lune, l’impesanteur est supposée être momentanément réalisée à l’intérieur du véhicule spatial.
On dispose de deux instruments de mesure du temps : une horloge à balancier et une montre à quartz. Ces deux appareils fonctionnent-ils correctement ? Justifiez votre réponse.
Même question après l’arrivée sur la Lune.