; 
; 
Echanges radiatifs entre surfaces grises séparées par un milieu parfaitement transparent
Plan
1. Echanges radiatifs entre deux surfaces noires
1.1. Calcul des facteurs de forme
1.2. Représentation des échanges radiatifs
entre surfaces noires par analogie électrique
2. Echanges radiatifs entre deux surfaces opaques grises
diffusantes
L’air exempt de vapeur d’eau, de dioxyde de carbone et de monoxyde de
carbone peut être considéré comme un milieu transparent.
Compte tenu de ce que nous savons sur l’émissivité, sur
les coefficients d’absorption de réflexion et de transmission, le
calcul des échanges radiatifs entre surfaces devient vite complexe.
Aussi, nous limitons nos propos aux surfaces grises et diffusantes (aussi
bien en émission qu’en réflexion) qui obéissent donc
à la loi de Lambert et dont le comportement radiatif est identique
quelque soit la longueur d’onde.
1. Echanges radiatifs entre deux surfaces noires
Pour ce type de surfaces :
; ;
Le flux radiatif émis par la surface 
en direction de la surface 
est égale à :
où 
si 
est la
température de la surface 
et
, appelé
facteur de forme de 1à 2, représente
la fraction de flux émis par
qui atteint .
On remarquera que le facteur de forme a un caractère purement
géométrique.
De même, le flux radiatif émis par la surface 
en direction de la surface 
est égale à :
où 
si 
est la
température de la surface 
et
, appelé
facteur de forme de 2à 1, représente
la fraction de flux émis par
qui atteint 
.
La relation de réciprocité 
est générale,
si bien que dans le cas d’échanges entre plusieurs surfaces on écrit 
Les surfaces étant noires, le flux 
est entièrement absorbé par la surface 2, de même le flux 
est entièrement absorbé par la surface 1.
Le flux net échangé par la surface 1 est égal à 
et la densité de flux échangé est égal à 
.
Remarque : par convention, dans la plupart des ouvrages de rayonnement, on compte positivement les pertes d’énergie d’une surface.
1.1. Calcul des facteurs de forme
),
l’opérateur intégrale étant un opérateur linéaire,
on obtient la relation
 |
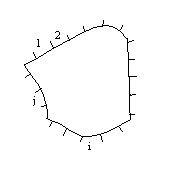Soit une surface fermée constituée de
surfaces noires individuellement isothermes, au nombre de  .
Pour la ième surface, on
peut définir
Soit
|
Remarque : il est toujours possible de considérer que plusieurs surfaces en présence constituent une surface fermée en comblant au besoin les espaces vides par des surfaces fictives pour lesquelles la température est celle du milieu ambiant.
 |
;  ; 
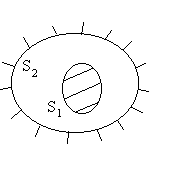Le lecteur adaptera les résultats ci-dessus au cas de deux sphères,
de deux cylindres très longs, de deux plans infinis parallèles,
d’une demi-sphère ou d’un demi-cylindre très long avec leur
plan de base de surface |
Remarque : le lecteur trouvera en annexe, à la fin du chapitre des expressions analytiques des facteurs de forme pour des géométries simples et des abaques pour l’évaluation des facteurs de forme.
1.2. Représentation des échanges radiatifs entre surfaces noires par analogie électrique
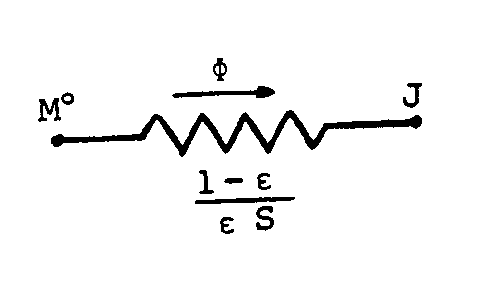
La relation exprimant le flux net échangé entre deux surfaces
noires 
, à
savoir 
est analogue à celle 
donnant le courant électrique qui s’établit entre deux nœuds de
potentiels 
reliés par la résistance 
.
Le calcul du potentiel " flottant " 
se fait simplement en écrivant que le flux radiatif échangé
par la surface adiabatique est nul.
ð |
 |
2. Echanges radiatifs entre deux surfaces opaques grises diffusantes
Ce type de surface, outre le flux radiatif émis, réfléchit
une partie du flux radiatif incident (qu’elle reçoit).
On introduit une nouvelle grandeur 
,
appelée radiosité, constituée du flux émis
et du flux réfléchi c’est à dire du flux qui " quitte la
surface ".
où 
est l’éclairement.
L’émissivité 
est relative au rayonnement émis alors que le coefficient de réflexion 
dépend du rayonnement incident.
L’introduction de la grandeur radiosité prend tout son intérêt
pour des surfaces grises où ses coefficients ont des valeurs " indépendantes
" de la nature des rayonnements émis et incident.
Ainsi, on peut écrire 
ð
pour des surfaces opaques, soit 
Le flux radiatif échangé par une surface 
est égal à 
différence entre celui émis et celui absorbé.
Cas d’une enceinte (surface fermée)
La surface fermée est constituée de
surfaces 
.
La radiosité 
de la surface 
est égale à l’émittance propre de cette surface augmentée
de la partie réfléchie, par unité de surface, du flux en
provenance de toutes les surfaces (y compris
si cette surface est concave).
L’ émittance propre de 
est égale à 
Le flux incident sur 
est égale à 
soit par unité de surface 
et 
On obtient l’équation 
exploitable si l’on connaît 
.
Si, pour la surface considérée, la donnée est la densité
de flux échangé (exemple : surface adiabatique 
),
alors 
On obtient ainsi un système de
équations linéaires qui permettent de calculer les
radiosités et , en conséquence, les températures ou les
flux échangés à partir de la relation 
.
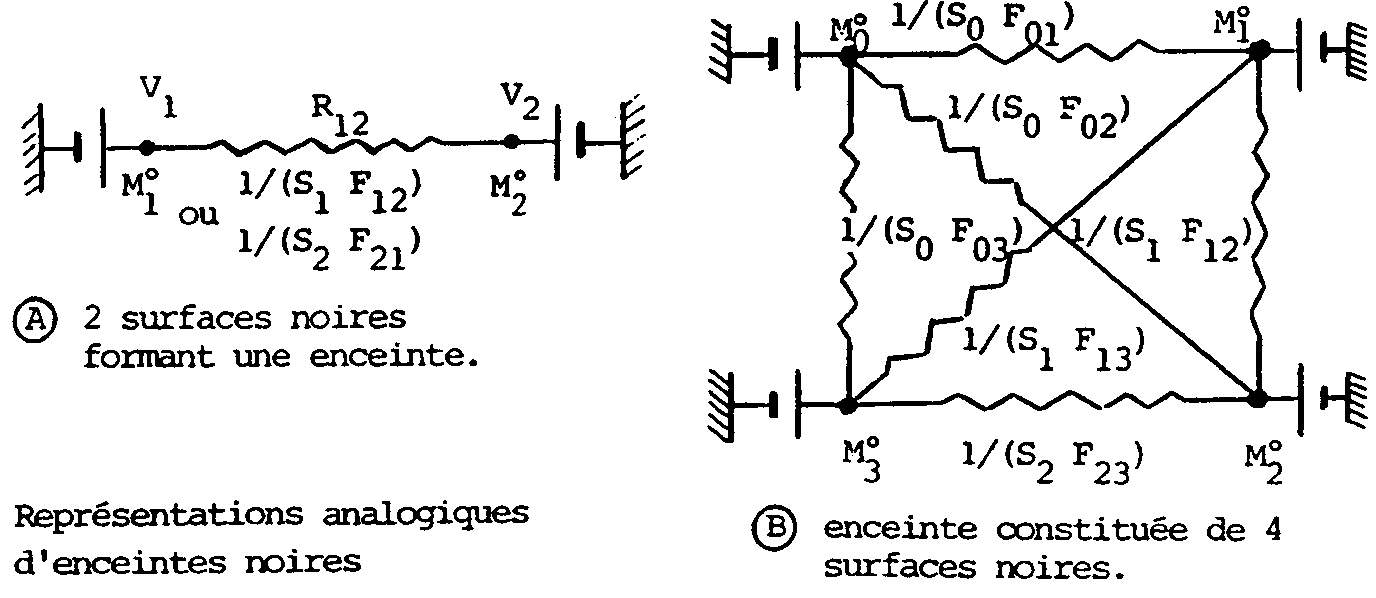
Représentation des échanges radiatifs par analogie
électrique
|
|
 |
|
Le flux total quittant la surface
|
 |
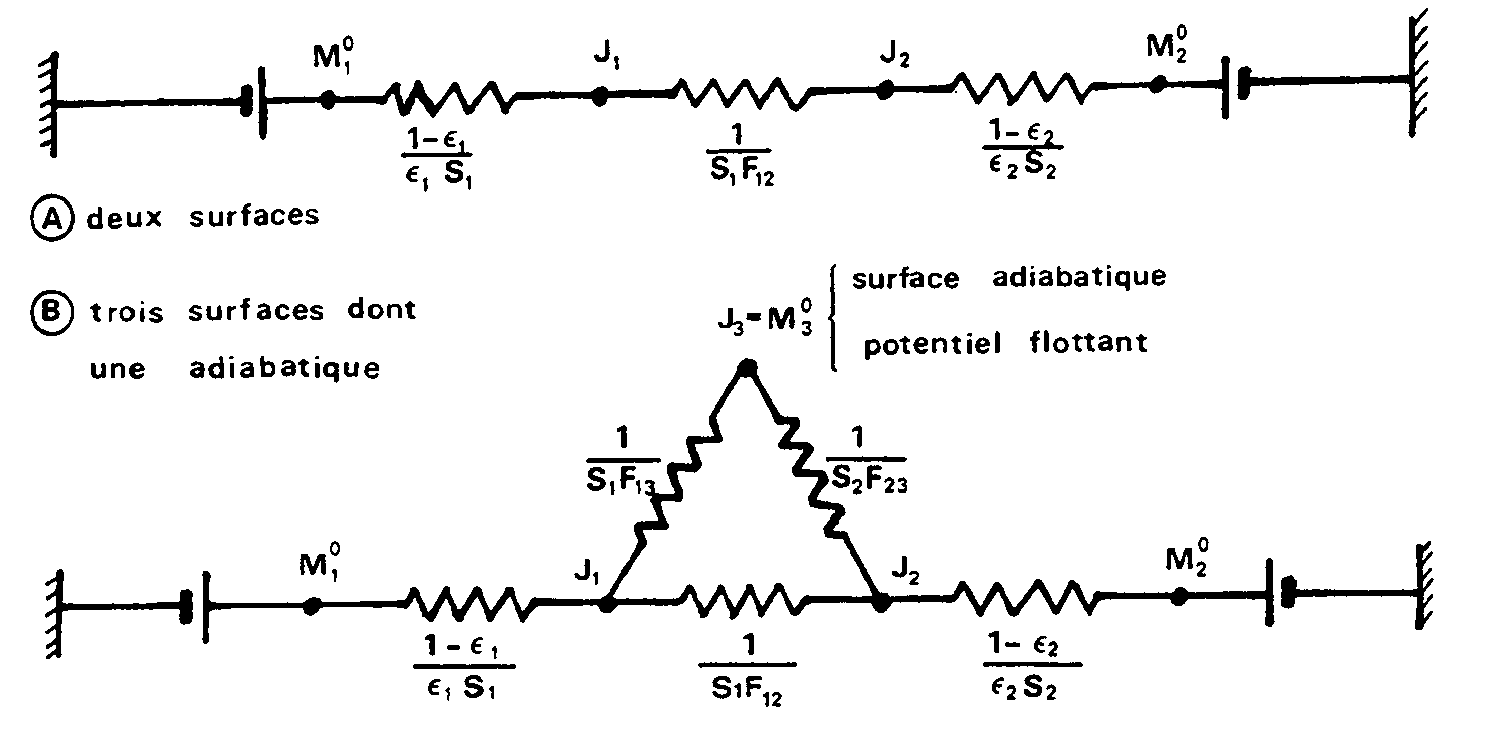
Pour un petit nombre de surfaces (2, 3 avec conditions particulières
de type surface adiabatique ou surface noire ou surface de grande étendue),
l’utilisation de l’analogie électrique est rapide et préférable
à celle de la résolution du système d’équations
linéaires.
Ainsi pour deux surfaces (cas A), on obtient :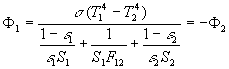 
où 
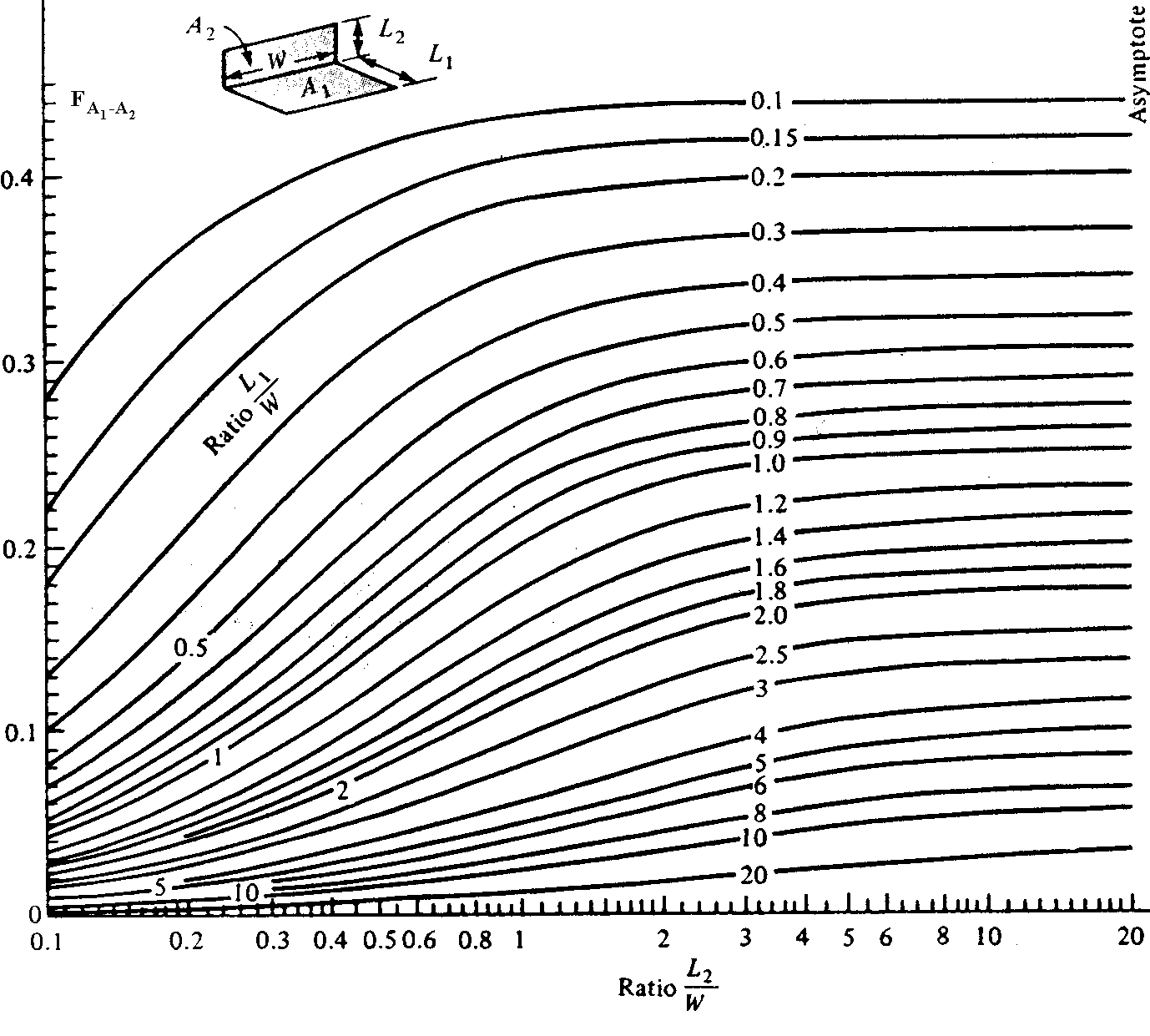
Expressions analytiques pour des géométries simples
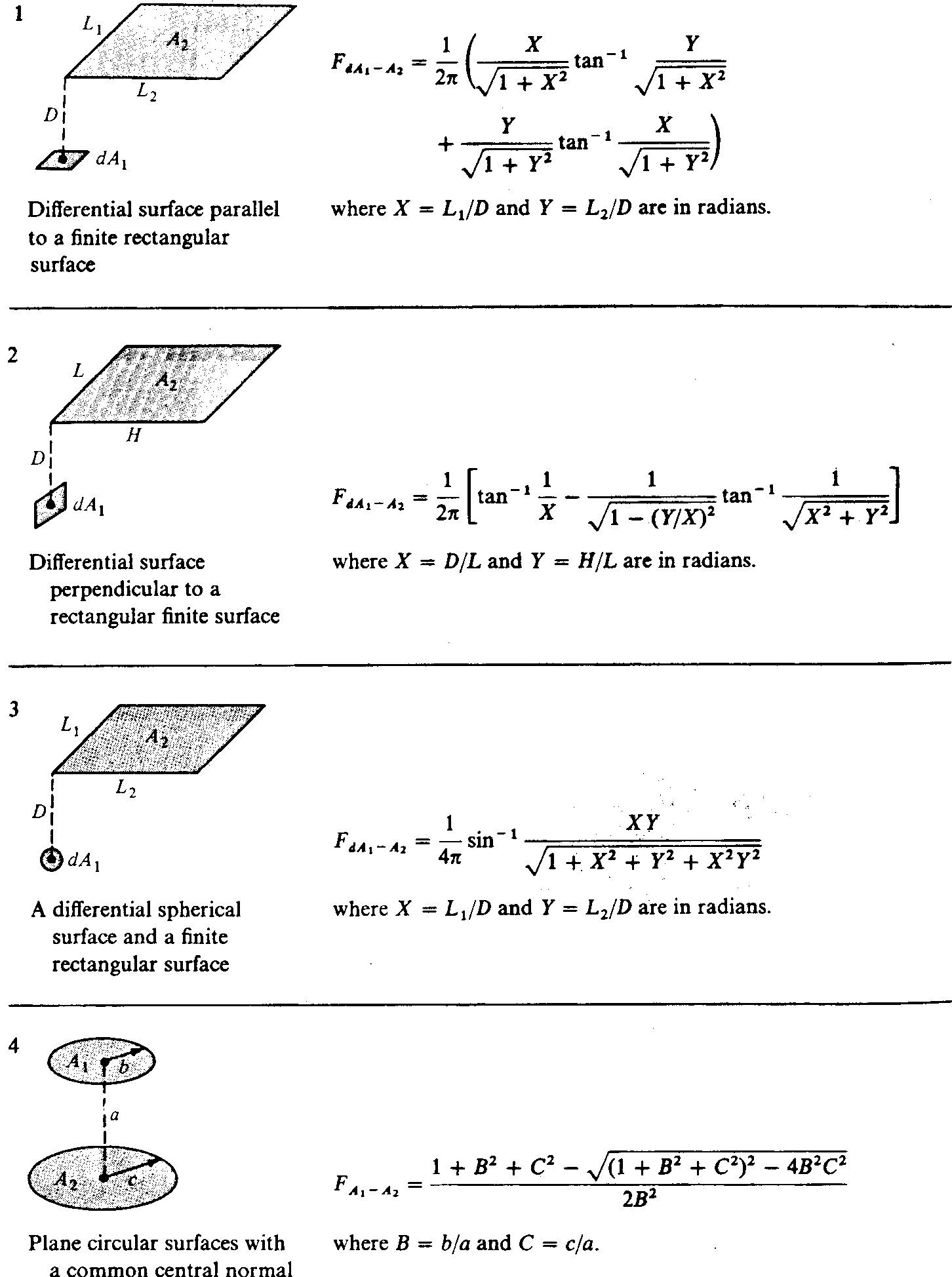
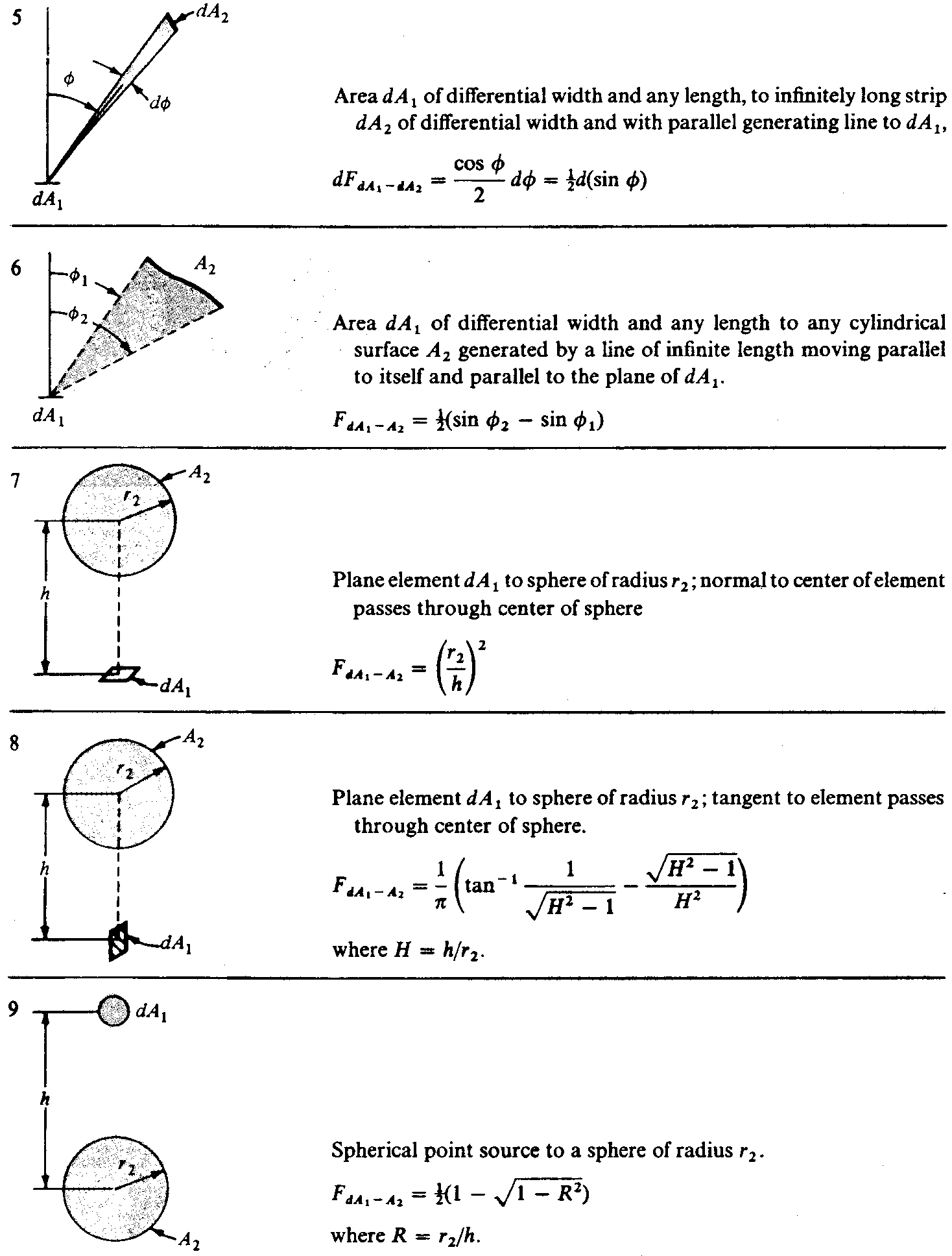
Abaques pour l’évaluation des facteurs de forme
Ratio 
.
est le facteur
de forme de la surface 
le flux émis par la surface 
.
ð
ð
,
celui atteignant 
est égale à 
De même, celui quittant 
est égale à 
.
Le flux échangé est donc : 
ð