Définitions et lois du rayonnement Thermique
Plan
1. Définitions
1.1. Luminance monochromatique et luminance (totale)
1.2. Intensité monochromatique et intensité (totale)
1.3. Emittance monochromatique et émittance (totale)
2. Les lois régissant l’émission du rayonnement
thermique
2.1. Relation entre luminance et émittance dans le cas
d’une émission diffuse (ou isotrope)
2.2. Le corps noir
2.2.1. Loi de Planck
2.2.2. Approximations de la loi de Planck : lois de Wien
2.2.3. Loi de Stefan-Boltzmann
2.3. Emission des corps réels
3. Réflexion, absorption et transmission du rayonnement
par un corps
3.1. Réalisation d'un corps noir
3.2. Relation entre absorption et émission : loi de Kirchhoff
3.3. Coefficient de transmission
4. Eclairement (irradiance) monochromatique et éclairement (total)
Le soleil qui se situe à une distance considérable
dans le " vide spatial " nous procure une sensation de chaleur. De
même, si nous ouvrons la porte d'un four en fonctionnement, nous percevons
une sensation de chaleur instantanée que nous ne pouvons attribuer
à un transfert convectif du à l'air entre le four et notre peau.
Cet échange de chaleur attribué à l'émission, par
la matière du fait de sa température, d'ondes électromagnétiques
est appelé rayonnement thermique, il ne nécessite pas la
présence d'un milieu intermédiaire matériel.
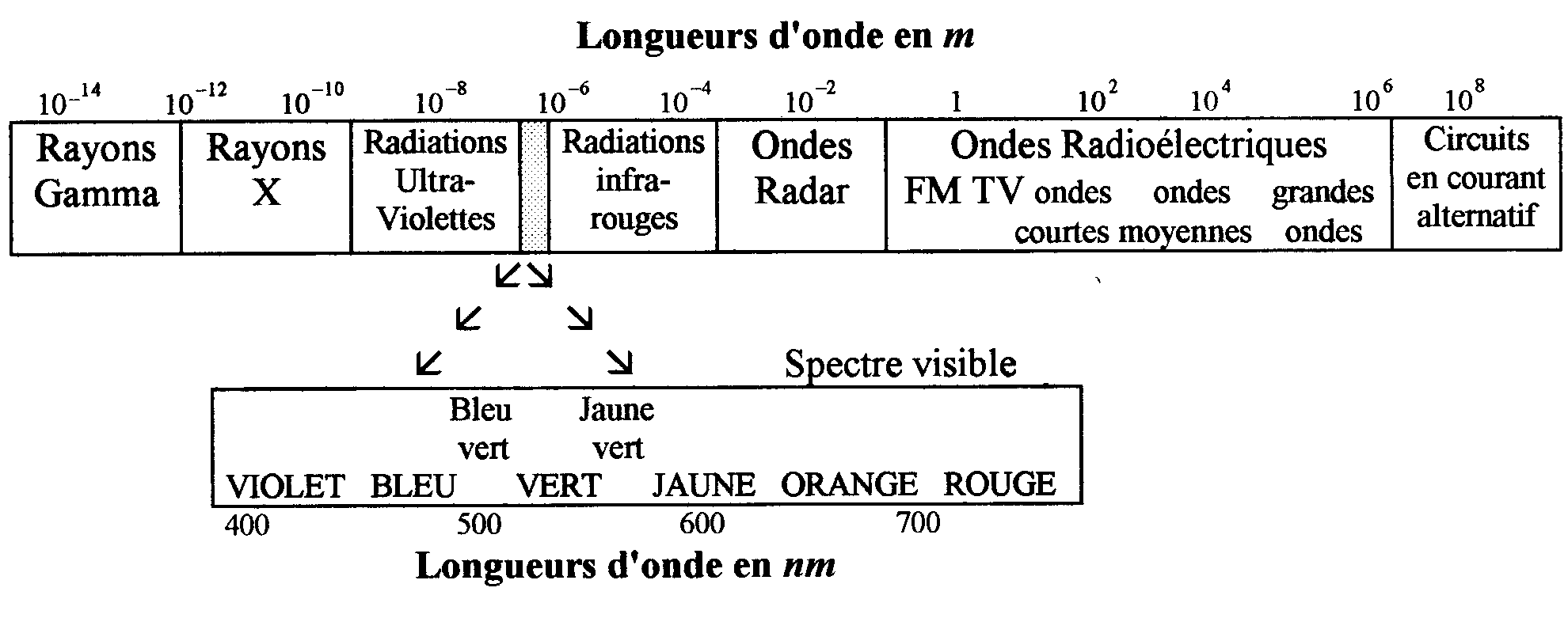
Le rayonnement thermique est caractérisé par des longueurs d'ondes
comprises entre 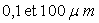 ,
il inclut le domaine du visible (ondes lumineuses ou lumière de
,
il inclut le domaine du visible (ondes lumineuses ou lumière de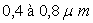 )
et n'occupe qu'une faible portion du spectre d'ondes électromagnétiques.
)
et n'occupe qu'une faible portion du spectre d'ondes électromagnétiques.
Remarque : bien qu'il soit plus avantageux de rapporter les grandeurs
monochromatiques à la fréquence 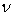 qui est indépendante du milieu matériel transparent où
l'onde se propage, l'habitude est de se référer à la longueur
d'onde
qui est indépendante du milieu matériel transparent où
l'onde se propage, l'habitude est de se référer à la longueur
d'onde 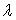 qui dépend
de l'indice
qui dépend
de l'indice 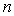 du
milieu (
du
milieu (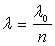 où
où
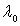 est la longueur
d’onde dans le vide; pour l'air
est la longueur
d’onde dans le vide; pour l'air 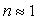 ).
Cette manière de faire ne présente d'inconvénient majeur
que pour les milieux semi-transparents non homogènes.
).
Cette manière de faire ne présente d'inconvénient majeur
que pour les milieux semi-transparents non homogènes.
1. Définitions
1.1. Luminance monochromatique et luminance (totale)
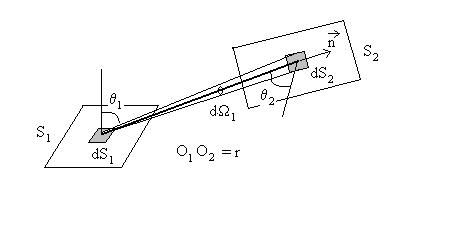
 sont des surfaces élémentaires respectivement des surfaces
sont des surfaces élémentaires respectivement des surfaces  de deux corps radiants.
de deux corps radiants.  représente la distance entre les deux surfaces élémentaires.
représente la distance entre les deux surfaces élémentaires.
Le flux énergétique monochromatique radiant 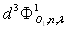 émis par la surface
émis par la surface 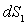 en direction de la surface
en direction de la surface 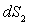 (direction
(direction 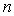 , dans
la bande monochromatique [
, dans
la bande monochromatique [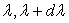 ]
est égale à :
]
est égale à :
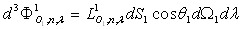 où
où 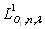 est la luminance monochromatique de la surface
est la luminance monochromatique de la surface 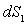 et où
et où 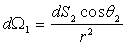 est l’angle solide sous lequel est vu, de
est l’angle solide sous lequel est vu, de 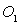 ,
la surface
,
la surface 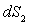 .
.
On obtient la formule fondamentale dite de Bouguer : 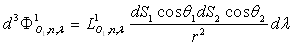
De manière analogue, on définit la luminance
monochromatique émis par la surface 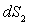 en direction de la surface
en direction de la surface 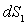 .
.
La quantité 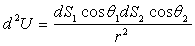 est appelée étendue spatiale élémentaire du faisceau
en Optique, elle est conservée à la traversée des instruments
optiques.
est appelée étendue spatiale élémentaire du faisceau
en Optique, elle est conservée à la traversée des instruments
optiques.
La luminance (totale), dans la direction 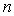 ,
est définie par
,
est définie par 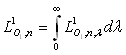 .
.
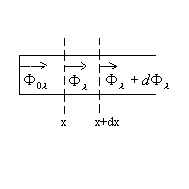
Il est commode d’écrire le flux énergétique
monochromatique, dans la direction 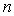 sous la forme :
sous la forme : 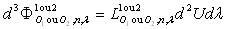 et le flux énergétique (total) sous la forme :
et le flux énergétique (total) sous la forme : 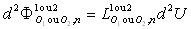
1.2. Intensité monochromatique et intensité
(totale)
L’intensité monochromatique est définie
par la relation 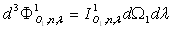 ,
elle est liée à la luminance monochromatique par la relation
,
elle est liée à la luminance monochromatique par la relation 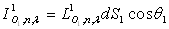 .
.
L’intensité (totale) est égale à 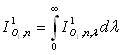
1.3. Emittance monochromatique et émittance (totale)
L’émittance monochromatique est définie
par 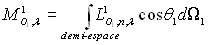 .
.
La quantité 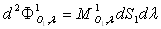 représente le flux énergétique monochromatique radiant
émis par la surface
représente le flux énergétique monochromatique radiant
émis par la surface 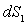 dans toutes les directions c’est à dire dans le demi-espace vu de
dans toutes les directions c’est à dire dans le demi-espace vu de 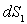 .
.
L’émittance (totale) est égale à 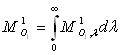
2. Les lois régissant l’émission
du rayonnement thermique
2.1. Relation entre luminance et émittance
dans le cas d’une émission diffuse (ou isotrope)
On dit que l’émission est diffuse (ou isotrope) si la
luminance est indépendante de la direction 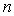 .
On dit que la source émettrice obéit à la loi de Lambert.
.
On dit que la source émettrice obéit à la loi de Lambert.
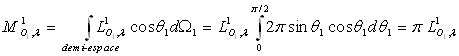
La démonstration étant identique, émittance totale et luminance
totale vérifie une relation de même forme, soit 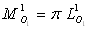 .
.
2.2. Le corps noir
L’émetteur " idéal " qui rayonnerait un maximum d’énergie
à chaque température et pour chaque longueur d’onde est appelé
corps
noir.
Nous verrons qu’on évalue l’énergie émise par
les différents corps par comparaison à celle qu’émettrait
le corps noir dans les mêmes conditions en introduisant un coefficient
appelé émissivité.
2.2.1. Loi de Planck
La loi de Planck donne la luminance monochromatique du corps
noir : 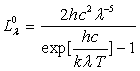
où 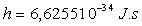 est la constante de Planck,
est la constante de Planck,
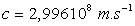 est la vitesse des ondes électromagnétiques dans le vide,
est la vitesse des ondes électromagnétiques dans le vide,
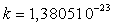 la constante de Boltzmann.
la constante de Boltzmann.
La luminance monochromatique du corps noir obéit à
la loi de Lambert ð 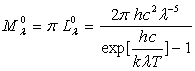
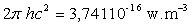 ;
;
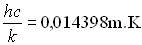
Remarque : dans le cadre de ce cours, il ne saurait
être question de justifier la loi de Planck qui fait appel à des
notions de quantification et de Thermodynamique statistique.
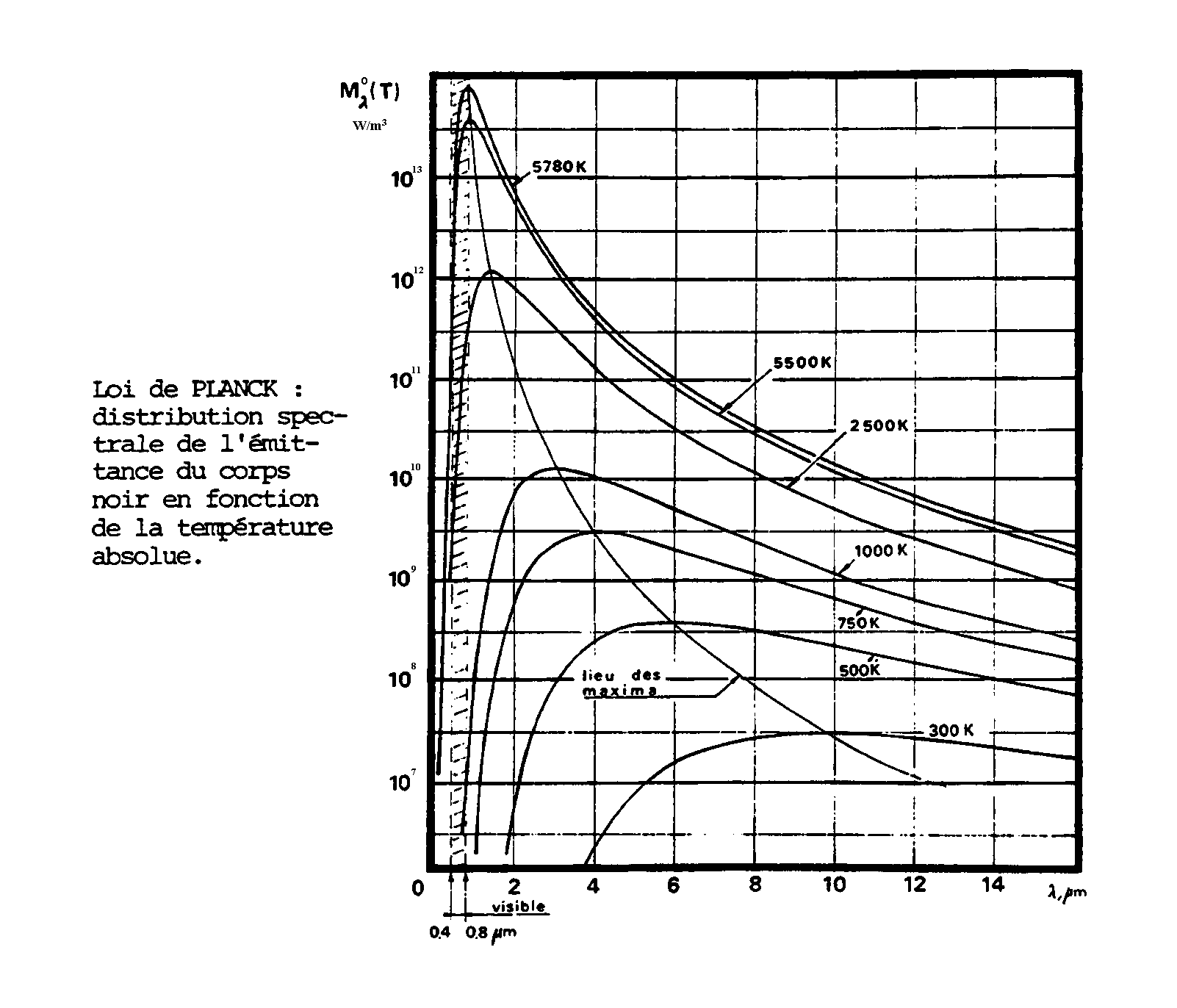
La figure ci-après donne une représentation de la loi de Planck.
A chaque température correspond une courbe ayant un maximum situé
à une valeur 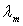 de la longueur d’onde variable avec
de la longueur d’onde variable avec 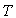 .
La courbe relative à une température
.
La courbe relative à une température 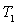 est toujours située au-dessus de celle correspondant à une température
est toujours située au-dessus de celle correspondant à une température
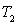 inférieure
à
inférieure
à 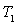 .
.
La croissance avec la longueur d’onde est beaucoup plus rapide que la décroissance.
2.2.2. Approximations de la loi de Planck : lois de Wien
La formule de Planck peut être approchée par 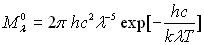 dite formule de Wien si
dite formule de Wien si 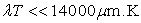 .
.
1ère loi de Wien : 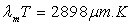
2ème loi de Wien : 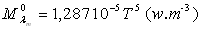
Remarques
- Le déplacement de
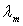 vers les courtes longueurs d’onde, lorsque
vers les courtes longueurs d’onde, lorsque 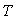 croît, explique le fait que, pendant son échauffement, un corps
n’émet d’abord que dans l’infra-rouge (radiations non-visibles), puis
commence à rougir avant de blanchir (" chauffé au
rouge " ou " chauffé à blanc ")
croît, explique le fait que, pendant son échauffement, un corps
n’émet d’abord que dans l’infra-rouge (radiations non-visibles), puis
commence à rougir avant de blanchir (" chauffé au
rouge " ou " chauffé à blanc ")
- Il n’y a pratiquement pas de recouvrement entre la partie utile du spectre
du rayonnement solaire (
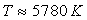 )
et celui d’un corps de température peu supérieure à l’ambiante ;
cette propriété est exploitée dans des applications de
type serres, vérandas, capteurs solaires, …
)
et celui d’un corps de température peu supérieure à l’ambiante ;
cette propriété est exploitée dans des applications de
type serres, vérandas, capteurs solaires, …
2.2.3. Loi de Stefan-Boltzmann
La luminance totale est obtenue par intégration à
toutes les longueurs d’onde de la luminance monochromatique, soit 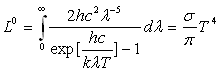 ,
l’émittance totale étant égale à
,
l’émittance totale étant égale à 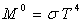 .
.
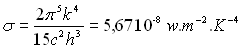 est la constante de Stefan-Boltzmann
est la constante de Stefan-Boltzmann
La loi de Stefan-Boltzmann peut être trouvée par
des considérations de Thermodynamique classique. L’accord entre résultats
théorique et expérimental est excellent puisqu’expérimentalement
on s’accorde sur 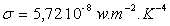
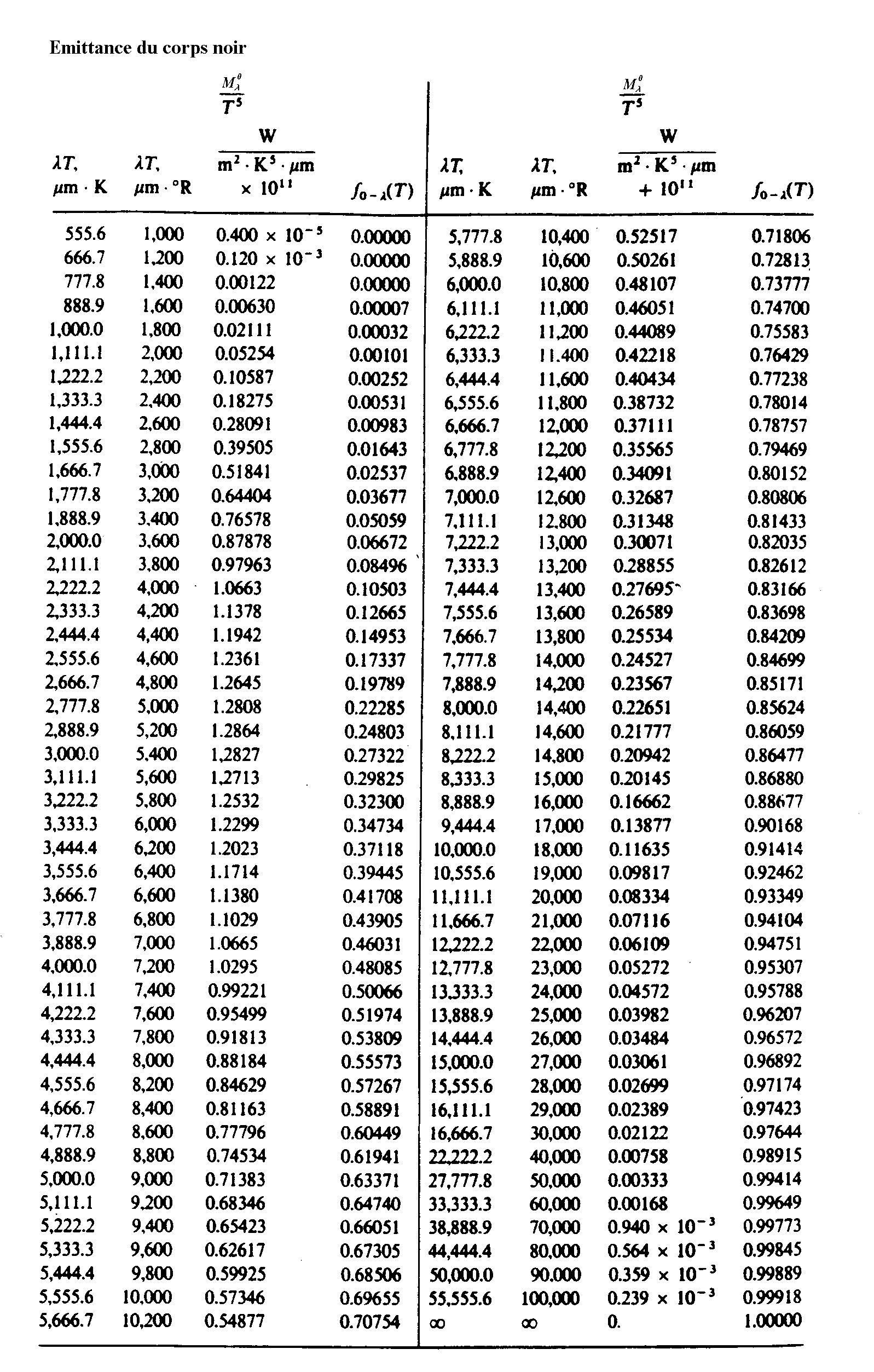
Fraction d’émittance totale dans un intervalle monochromatique
donné
On a souvent besoin d’évaluer, à une température
donnée, la quantité :
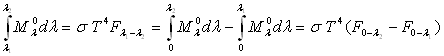
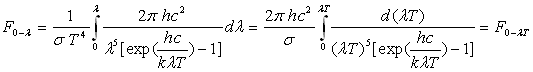
Nous donnons dans le tableau ci-après quelques valeurs
caractéristiques de 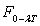 .
Le lecteur trouvera, à la fin du chapitre, un tableau très complet
de l’émittance du corps noir ainsi que de
.
Le lecteur trouvera, à la fin du chapitre, un tableau très complet
de l’émittance du corps noir ainsi que de 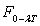 .
.
|
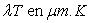
|
1449
|
2898
|
4108
|
6149
|
23220
|
|
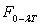
|
1%
|
25%
|
50%
|
75%
|
99%
|
Ainsi, il n’y a pratiquement plus d’énergie rayonnée
(moins de 1%) pour 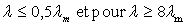
2.3. Emission des corps réels
L’évaluation des propriétés émissives
des substances réelles se fait à partir de celles du corps noir
placé dans les mêmes conditions de température et de longueur
d’onde à l’aide de coefficients appelés émissivités,
monochromatiques ou totales, directionnelles ou hémisphériques.
On définit :
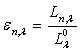 : émissivité
monochromatique directionnelle
: émissivité
monochromatique directionnelle
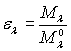 : émissivité
monochromatique hémisphérique
: émissivité
monochromatique hémisphérique
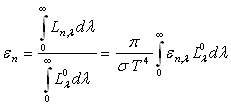 : émissivité
totale directionnelle
: émissivité
totale directionnelle
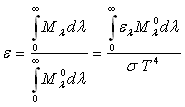 :
émissivité totale hémisphérique
:
émissivité totale hémisphérique
L’émissivité des substances dépend de
leur nature physico-chimique, de leur état de surface ; elle varie
avec la longueur d’onde, la direction d’émission et la température
de surface.
|
|
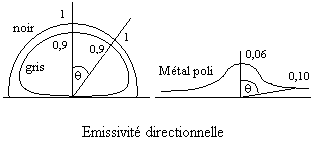
On met en évidence deux grandes classes de comportements
radiatifs : celle des matériaux conducteurs de l’électricité
(métaux) et celle des isolants électriques (diélectriques).
|
Pour la première classe, l’émissivité
est faible sauf dans les directions rasantes à la surface où elle
est plus importante. L’émissivité monochromatique décroît
lorsque 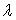 augmente et croît
lentement avec la température.
augmente et croît
lentement avec la température.
Pour la deuxième classe, l’émissivité est forte. Elle augmente
avec 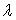 , elle suit
relativement bien la loi de Lambert sauf pour les directions rasantes à
la surface où elle diminue notablement.
, elle suit
relativement bien la loi de Lambert sauf pour les directions rasantes à
la surface où elle diminue notablement.
Définitions :
- corps gris : l’émissivité est indépendante
de la longueur d’onde
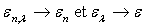
- corps à émission diffuse (ou isotrope) : l’émissivité
est indépendante de la direction
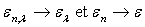
- corps gris et diffusant : l’émissivité est indépendante
de la longueur d’onde et de la direction ð
paramètre unique
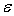
Remarque : sauf précision contraire, nous
ne considérerons que des corps gris diffusants.
3. Réflexion, absorption et transmission
du rayonnement par un corps
3.1. Réalisation d’un corps noir
3.2. Relation entre absorption et émission : loi de Kirchhoff
Le flux radiatif émis par l’élément 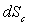 du corps en direction de l’enceinte est égal à :
du corps en direction de l’enceinte est égal à :
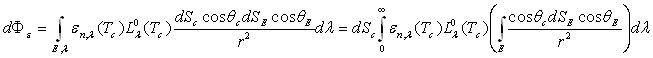
Le corps est en équilibre thermique ð
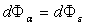 et par suite
et par suite
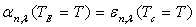 puisque
puisque 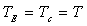 .
.
Par intégration, cette relation est vraie pour les coefficients
d’absorption et les émissivités hémisphériques monochromatiques
ou totaux, soient 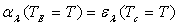 et
et 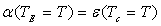
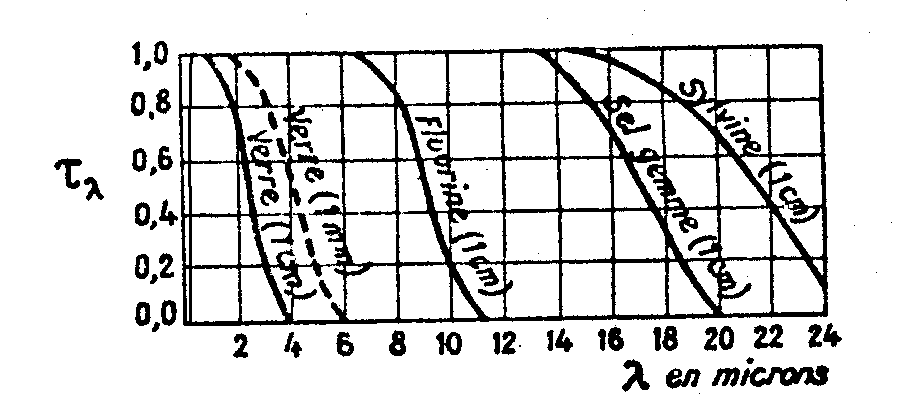
3.3. Coefficients de transmission
Le coefficient de transmission, pour une lame d’épaisseur
l est donc égal à 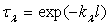 et le coefficient d’absorption si les réflexions sont négligeables
sur les faces d’entrée et de sortie de la lame à
et le coefficient d’absorption si les réflexions sont négligeables
sur les faces d’entrée et de sortie de la lame à 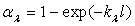 .
.
En fait, dans la littérature, on ne trouve généralement
pas les valeurs de 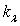 mais celles de
mais celles de 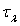 ou de
ou de 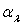 en fonction
de l pour une épaisseur donnée
l de la substance.
en fonction
de l pour une épaisseur donnée
l de la substance.
Le cas de l'air
L'air est principalement constitué :
- de molécules diatomiques de O2 et de N2 transparentes
pour toute longueur d'onde,
- mais aussi de molécules triatomiques (O3 , CO2
, H2O) voir plus complexes comme CH4 .
Ces dernières molécules sont absorbant pour certaines
longueurs d'ondes,
- O3 pour
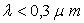 (ultraviolet)
(ultraviolet)
- CO2 pour
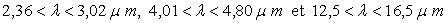
- H2O pour
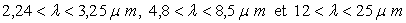
- CH4 pour l'infrarouge
Le coefficient d'absorption pour chacun de ces gaz augmente
avec le produit 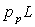 où
où 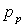 est
la pression partielle du gaz et L la longueur traversée.
est
la pression partielle du gaz et L la longueur traversée.
Remarque :
- Ces propriétés des corps semi-transparents expliquent le fonctionnement
thermique des serres, des vérandas.
- Elles expliquent aussi la pollution thermique atmosphérique (l'augmentation,
dans l'atmosphère, de molécules de CO2 voire de CH4
d'origine industrielle et anthropique provoque une absorption de plus en plus
importante du rayonnement thermique de la Terre dont la conséquente
est l'augmentation de sa température).
4. Eclairement (irradiance) monochromatique et éclairement
(total)
L’éclairement monochromatique appelé aussi
irradiance est défini par la relation :
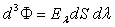 où
où 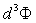 est
le flux énergétique et
est
le flux énergétique et 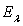 l'éclairement monochromatique (spectral) de l'élément
de surface dS.
l'éclairement monochromatique (spectral) de l'élément
de surface dS.
L’éclairement (total) sera défini par
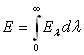 .
.
Ainsi l’éclairement monochromatique d'un récepteur
situé en 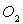 par un émetteur situé en
par un émetteur situé en 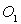 en supposant que le milieu intermédiaire est parfaitement transparent
est égal à :
en supposant que le milieu intermédiaire est parfaitement transparent
est égal à :
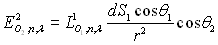 puisque
puisque 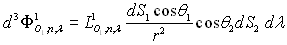
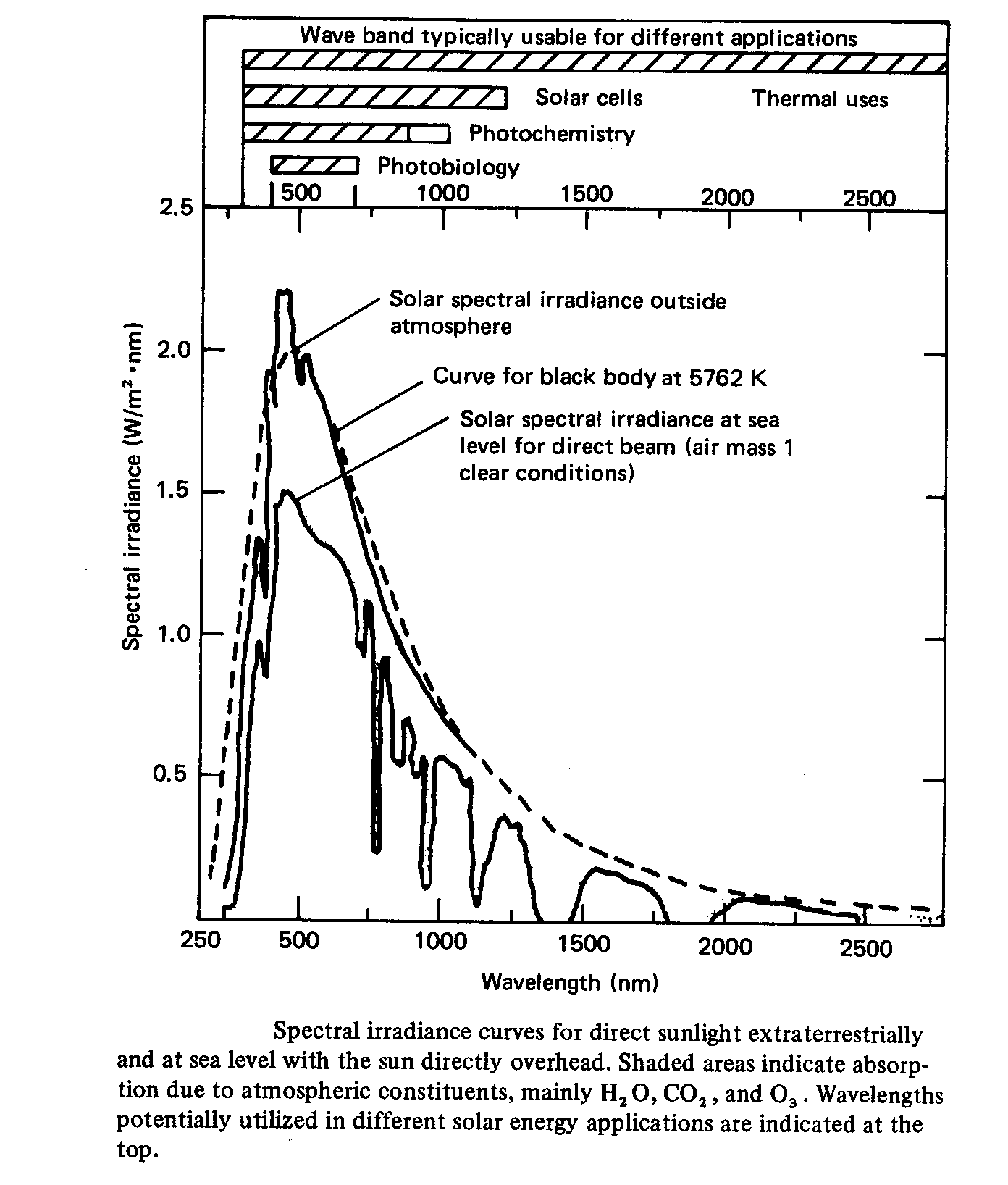
La courbe ci-après donne l'allure de l'éclairement
de la terre par le Soleil en tenant compte de l'absorption par l'air atmosphérique.


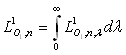 .
.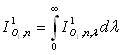
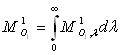
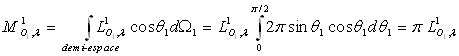
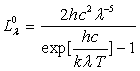
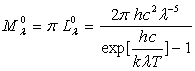

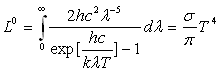 ,
l’émittance totale étant égale à
,
l’émittance totale étant égale à 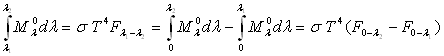
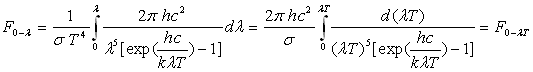
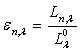 : émissivité
monochromatique directionnelle
: émissivité
monochromatique directionnelle
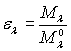 : émissivité
monochromatique hémisphérique
: émissivité
monochromatique hémisphérique
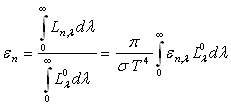 : émissivité
totale directionnelle
: émissivité
totale directionnelle
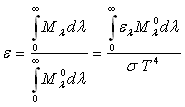 :
émissivité totale hémisphérique
:
émissivité totale hémisphérique

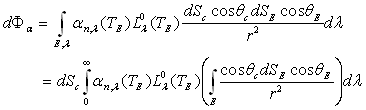
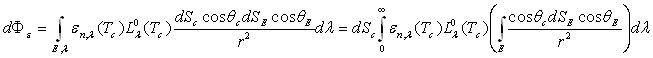

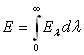 .
.
