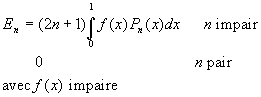Annexe 1 : Fonctions de Bessel - Polynômes de Legendre

En Conduction de la Chaleur, on est souvent amené à résoudre des équations différentielles linéaires du second ordre. Le cas où les coefficients sont constants est classique.
Pour des coefficients variables, nous limitons nos propos à des solutions qui font appel aux fonctions de Bessel ou aux polynômes de Legendre. Ces cas correspondent à des solutions exprimables en séries de puissance.

1. Exemple
Soit l’équation différentielle  pour laquelle on cherche une solution sous la forme .

En reportant dans l’équation, on obtient , soit 
Evidemment les deux séries obtenues ne sont autres que les développements de Mac Laurin de  et .
On notera, aussi, que le développement en série n’a de sens que, pour un intervalle de x, où la série est convergente.

2. Les fonctions de Bessel

2.1. Equation de Bessel

ð avec  entier, nul ou fractionnaire.

La fonction  est nommée fonction de Bessel de 1ère espèce d’ordre, la fonction  est nommée fonction de Bessel de 2ème espèce d’ordre.
On montre que si  est entier 

2.2. Equation de Bessel modifiée

ð

La fonction  est nommée fonction de Bessel modifiée de 1ère espèce d’ordre, la fonction  est nommée fonction de Bessel modifiée de 2ème espèce d’ordre .
Pour passer de l’équation de Bessel à celle modifiée, il suffit de changer m en im ().

ð.
On montre que si  est entier 

2.3. Equation différentielle 

Le changement de fonction  permet d’exprimer la solution à l’aide des fonctions de Bessel.
En effet, en choisissant tel que , on obtient , soit  pour le signe + et  pour le signe - .

2.4. Equation différentielle  où  sont positifs et  réel ou imaginaire

Le changement de variable  conduit à 

2.4.1. Si  on choisit  de telle sorte que 

On obtient  qui est l’équation du paragraphe 2.3.

La solution est donc  pour le signe + et  pour le signe - où  ,  et  .

2.4.2.

Pour ce cas particulier connu sous le nom " d’équation d’Euler ou d’équation de Cauchy ", l’équation différentielle devient .

La solution est  où  sont solutions de l’équation caractéristique .

2.5. Quelques propriétés des fonctions de Bessel

Dans nos propos,  représente une fonction de Bessel quelconque d’ordre  .

2.5.1. Dérivées

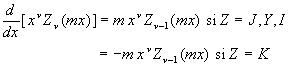
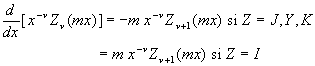
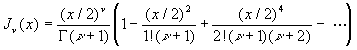
2.5.3. Valeurs asymptotiques des fonctions de Bessel (x ®¥ )

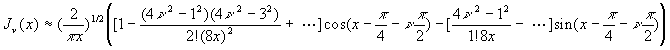
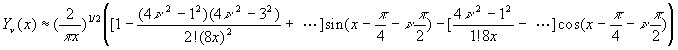
2.5.4. Relations entre quelques fonctions de Bessel et les fonctions trigonométriques ou hyperboliques

2.5.5. Représentation graphique de quelques fonctions de Bessel

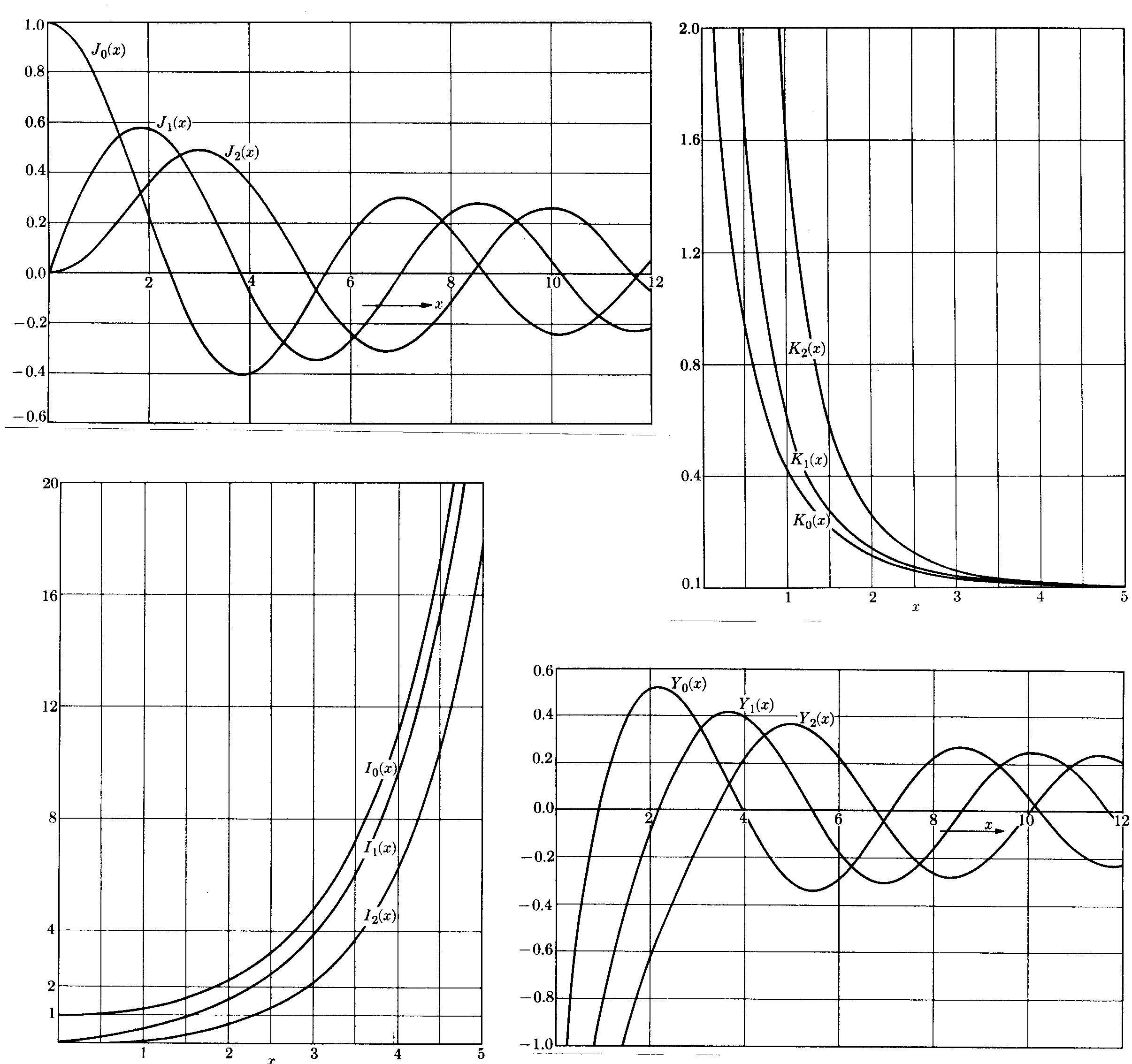
2.6. Quelques calculs classiques avec les fonctions de Bessel en Conduction de la chaleur

On a souvent à calculer l’expression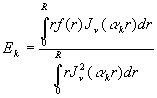 

• Pour le calcul du dénominateur, il convient de se rappeler que  est solution de.

En intégrant, cette équation devient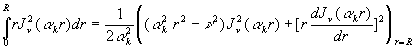 

Le calcul se continue à partir de la formule .

Trois cas se présentent suivant la forme de l’équation transcendante :

1)  est racine de ð

2)  est racine de ð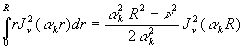

3)  est racine de ð

• Le calcul du numérateur nécessite la connaissance de . Dans un certain nombre de cas pratiques, le numérateur peut être calculé à partir de l’identité (directement déduite des formules de dérivation) .

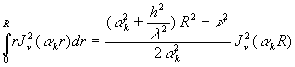
Exemples de tables de Fonctions de Bessel

3. Les polynômes de Legendre

3.1. Définition
L’équation différentielle linéaire du second ordre à coefficients variables  est connue sous le nom " d’équation de Legendre ". Ses solutions sont appelées " fonctions de Legendre ". Si n est nul ou entier positif, ces fonctions sont appelées " polynômes de Legendre ". Nos propos seront limités à ce seul cas.

Remarques :
- en Conduction de la chaleur, on rencontre l’équation de Legendre dans les problèmes sphériques à deux dimensions sous la forme  où .
- nous ne traitons pas ce cas mais, en Conduction de la chaleur dans les problèmes sphériques à trois dimensions, on rencontre les " polynômes associés de Legendre " qui satisfont l’équation différentielle :.

La solution de l’équation de Legendre (obtenable par la méthode des séries de puissance) s’écrit où sont respectivement les polynômes de Legendre de 1ére et de 2ème espèces de degré n.

3.2. Propriétés

3.2.1. Développements en séries de puissance des polynômes de Legendre

• si n est pair et supérieur ou égal à 2

si n est impair et supérieur ou égal à 3.

• Formule de Rodrigues

• si n est pair et supérieur ou égal à 2.

si n est impair et supérieur ou égal à 3.

• si bien que, sur un intervalle de variation pour x compris entre -1 et +1, la fonction ne présente pas de signification physique (le coefficient  est nul).

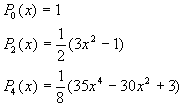
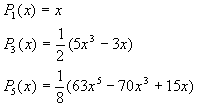
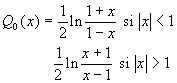
A partir de l’équation de Legendre, on montre sans peine que :

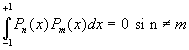
Calcul de 

Si f(x) et ses n premières dérivées sont continues dans l’intervalle [-1,+1]

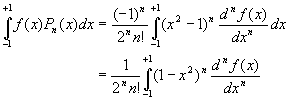
Le cas peut être traité simplement en utilisant la relation 

Le coefficient s’écrit alors 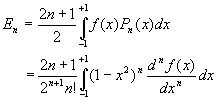 en remarquant que la deuxième forme ne peut être utilisée que si f(x) et ses n premières dérivées sont continues dans l’intervalle [-1,+1].
On remarquera que  est une fonction paire de x si n est pair et impaire de x si n est impair.

Par suite,