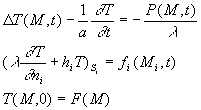
classique en Conduction de la chaleur. Les sources peuvent être constantes ou variables.
CHAPITRE 7 : Les régimes transitoires et variables par la méthode de la fonction de Green
Plan
1. Fonctions de Green associées aux problèmes
de Conduction de la Chaleur
2. Détermination de la fonction de Green
pour un problème donné
3. Exemples
4. Fonctions de Green associées à
l’équation de type " ailette "
1. Fonctions de Green associées aux problèmes de Conduction de la Chaleur
Nous considérons le système d’équations : 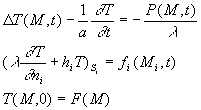
classique en Conduction de la chaleur. Les sources peuvent être constantes
ou variables.
Pour résoudre ce système, on considére les équations
: 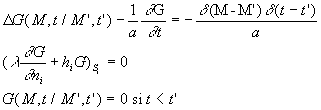
qui correspondent à la dissipation instantanée au temps
t’
d’une quantité de chaleur localisée en un point
M’, les sources externes étant toutes nulles c’est à
dire sans action.
La fonction ![]() traduit la réponse en température à une impulsion de chaleur
localisée, le langage généralement employé consiste
à parler d’effet en (M, t) du à la cause en (M’,
t’).
traduit la réponse en température à une impulsion de chaleur
localisée, le langage généralement employé consiste
à parler d’effet en (M, t) du à la cause en (M’,
t’).
L’effet est nul si ![]() puisque la cause ne s’est pas produite. En fait l’origine
puisque la cause ne s’est pas produite. En fait l’origine ![]() est arbitraire si bien que, dans la fonction G,
est arbitraire si bien que, dans la fonction G, ![]() et
et ![]() apparaissent
par le groupement
apparaissent
par le groupement ![]() qui
est la durée entre le moment où se produit la cause et le moment
où on examine l’effet.
qui
est la durée entre le moment où se produit la cause et le moment
où on examine l’effet.
D’autre part les fonctions de Green obéissent à la relation
de réciprocité de la cause et de l’effet à savoir![]() . Si la cause est produite en M, l’effet sera identique en M’
à condition, évidemment, de respecter la durée [
. Si la cause est produite en M, l’effet sera identique en M’
à condition, évidemment, de respecter la durée [![]() ].
].
************************************
Dans le calcul qui suit, on est amené à dériver par rapport
à M ou à M’. Pour le laplacien, on emploie respectivement
la notation D ou D’.
D’autre part ![]() puisque c’est le groupement
puisque c’est le groupement ![]() qui
apparait.
qui
apparait.
Ainsi ![]() et
et ![]()
On multiplie la première des équations par T, la seconde par G et on retranche membre à membre.
![]()
L’intégration sur la variable ![]() entre 0 et
entre 0 et ![]() (
(![]() infiniment petit
positif), sur la région R siège du phénomène
de Conduction de la Chaleur, conduit à :
infiniment petit
positif), sur la région R siège du phénomène
de Conduction de la Chaleur, conduit à :
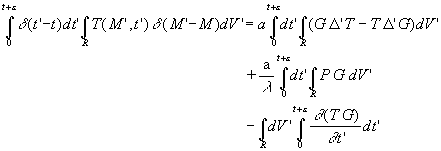
* 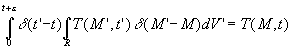
* ![]() (pour
la démonstration, voir ci-après ; la sommation doit être
faite à toutes les surfaces frontières de la région ; les
normales doivent être orientées vers l’extérieur)
(pour
la démonstration, voir ci-après ; la sommation doit être
faite à toutes les surfaces frontières de la région ; les
normales doivent être orientées vers l’extérieur)
On remarque que :
- pour une condition limite de première espèce (température
imposée), le terme entre parenthèse du deuxième membre
s’écrit ![]()
- pour une condition limite de deuxième espèce (flux imposé)
ou de troisième espèce (condition mixte), on peut écrire ![]() et
et ![]() si bien
que le terme entre parenthèse s’écrit :
si bien
que le terme entre parenthèse s’écrit :
![]()
* 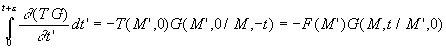 en se
rappelant que
en se
rappelant que![]() car
car ![]()
Ainsi en termes de fonctions de Green, la solution du problème de Conduction
peut être écrite :
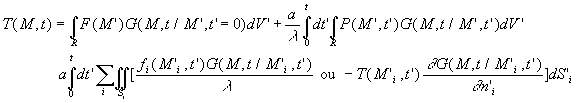
Démonstration
La relation ![]() et le théorème d’Ostrogradsky
et le théorème d’Ostrogradsky ![]() entraine
la formule de Green :
entraine
la formule de Green :
![]()
Remarques
Dans le chapitre 4 consacré au régime transitoire , on résout
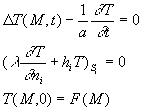 système
3
système
3
et on a vu que la solution s’exprime sous la forme ![]()
On sait donc déterminer la fonction ![]() ,
il suffira de remplacer
,
il suffira de remplacer ![]() par
par ![]() dans cette dernière fonction pour connaitre la fonction de Green
dans cette dernière fonction pour connaitre la fonction de Green ![]() associée
à un problème donné.
associée
à un problème donné.
3.1. Exemple 1
![]() . Ces équations
correspondent à un problème de mur avec distribution initiale
de température, puissance volumique dissipée et températures
imposées sur chacune des faces x = 0 et x = L. En x
= 0, le sens de la normale à cette face est opposé à
celle de la direction x, en x = L normale et direction x
sont de même sens.
. Ces équations
correspondent à un problème de mur avec distribution initiale
de température, puissance volumique dissipée et températures
imposées sur chacune des faces x = 0 et x = L. En x
= 0, le sens de la normale à cette face est opposé à
celle de la direction x, en x = L normale et direction x
sont de même sens.
Pour résoudre ce problème en terme de fonctions de Green,
on considére le système auxiliaire d’équations,
![]()
de solution 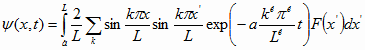
Par identification, on obtient ![]() et
en substituant
et
en substituant ![]() à
à ![]() la
fonction de Green associée au problème à savoir,
la
fonction de Green associée au problème à savoir,
![]()
La solution ![]() du
problème posé sera donc :
du
problème posé sera donc :
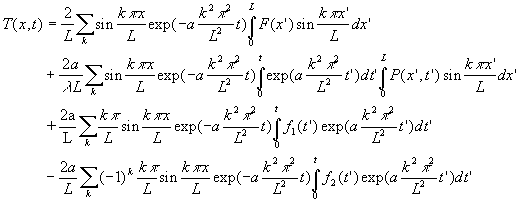
On envisage, en application, pour ![]() ,
,

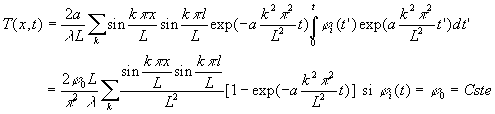
3.2. Exemple 2
Dans le paragraphe 2.1. du chapitre 4, il est noté que, pour
plusieurs directions d’espace, la fonction propre apparait comme un produit
des fonctions propres de chacune des directions.
Ce résultat reste vrai pour les fonctions de Green et le lecteur
pourra le vérifier sur l’exemple
![]()
qui conduit à ![]()
avec,
![]()
![]()
![]()
3.3. Exemple 3
![]()
On considère le système auxiliaire ![]() déjà étudié au paragraphe 6 chapitre 4.
déjà étudié au paragraphe 6 chapitre 4.
![]() ð
ð![]()
A titre d’exemple, on étudie, pour ![]() ,
la dissipation instantanée d’une quantité de chaleur au temps
t = 0 localisée sur la face x = L.
,
la dissipation instantanée d’une quantité de chaleur au temps
t = 0 localisée sur la face x = L.
![]() où Q
a la dimension d’une énergie par unité de surface.
où Q
a la dimension d’une énergie par unité de surface.
![]()
3.4. Exemple 4
Le milieu étant infini à symétrie sphérique,
on s’intéresse à la réponse à un point source
situé en r = 0.
Le problème auxiliaire s’écrit ![]() et on fait le changement
et on fait le changement ![]() qui transforme le problème à symétrie sphèrique
en un problème de mur.
qui transforme le problème à symétrie sphèrique
en un problème de mur.
![]()
Ce système a été étudié au paragraphe
5.3. chapitre 4, on a obtenu
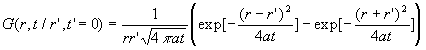
si bien que 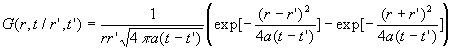
On envisage, en application, pour ![]() ,
le cas du point source qui dissipe instantanément une quantité
de chaleur Q ou qui dissipe continûment un flux de chaleur
,
le cas du point source qui dissipe instantanément une quantité
de chaleur Q ou qui dissipe continûment un flux de chaleur ![]() .
Dans les deux cas, les dissipations seront localisées sur la sphère
de rayon r = R et on fera tendre R vers 0 pour obtenir le point
source.
.
Dans les deux cas, les dissipations seront localisées sur la sphère
de rayon r = R et on fera tendre R vers 0 pour obtenir le point
source.
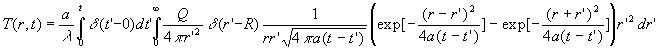
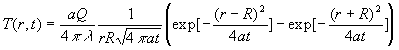
Pour résoudre le problème du point source à dissipation
instantanée, on fait tendre R vers 0 dans l’expression précédente
et on obtient 
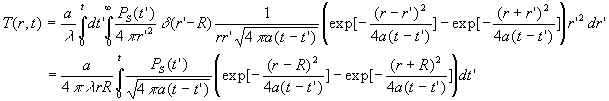
Dans cette dernière expression, on fait tendre R vers
0 et on obtient
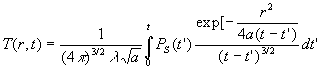
![]()
3.5. Exemple 5
![]() . Ce système
étudie le champ de température dans un cylindre cylindre plein.
. Ce système
étudie le champ de température dans un cylindre cylindre plein.
Le problème auxiliaire s’écrit :
![]()
L’équation transcendante est ![]() ,
la solution
,
la solution 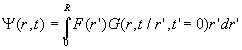 avec
avec ![]()
![]() est donc la
fonction de Green associée à ce problème et la solution
générale s’écrira :
est donc la
fonction de Green associée à ce problème et la solution
générale s’écrira :
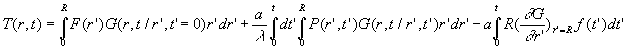
On n’envisage pas de valeurs particulières
4. Fonctions de Green associées à l’équation de type " ailette "
Pour résoudre le système 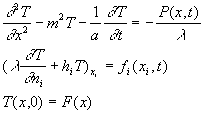
on étudie 
La théorie, qui n’est pas reproduite ici, est à " calquer
" sur celle présentée au paragraphe1. et la solution générale
s’écrit :
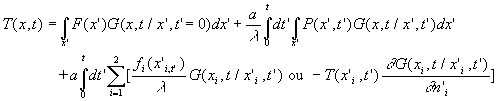
Cas de l’ailette semi-infinie soumise à une densité de flux de chaleur
On ne reproduit pas les calculs, la fonction de Green associée
est :
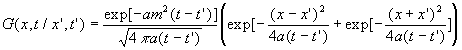
Pour une densité de flux de chaleur constante ![]() ,
on obtient :
,
on obtient :
![]()