1 PROLOGUE HISTORIQUE      Sommaire 

On attribue généralement au danois Erasmus Bartholinus la découverte de la biréfringence du Spath d'Islande. Ses expériences sont décrites dans un ouvrage intitulé: "EXPERIMENTA CRYSTALLI ISLANDICI" publié en 1670.

" Hujus cristalli examini cum ulterius incumberem, mirum & insolitum apparuit Phaenomenon, qvo objecta per id conspecta, non sicuti in aliis corporibus pellucidis, simplici imagine refracta exibirentur, sed Dupla."

Lorsque j'examinais plus longuement ce cristal, un phénomène merveilleux et insolite apparut, l'image des objets vus à travers celui-ci n'était pas unique comme avec les corps transparents ordinaires, mais double.

EXPÉRIENCES & DÉCOUVERTES

Un cristal rhomboédrique de spath d'Islande est à votre disposition dans un coffret placé dans le bac contenant la collection de cristaux biréfringents.

Manipulez délicatement, avec des mains propres, ce cristal fragile et précieux (prix d'achat 1993 = 800F) à l'intérieur du bac.

Une page d'extraits de ce texte est collée au fond du bac. Posez le cristal sur le texte pour découvrir la double réfraction.

Pivotez le cristal autour de l'axe vertical pour observer le déplacement de l'image "extraordinaire" autour de l'image "ordinaire" qui reste fixe. Posez le cristal sur la croix. En observant sous incidence normale, tournez le rhomboèdre pour vous placer dans l'une ou l'autre des situations ci-dessous.

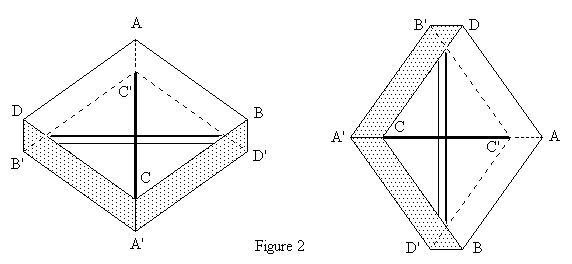
        Remarquez que le dédoublement semble disparaître lorsque l'un des traits de la croix est orienté suivant ou parallèlement à la bissectrice des angles obtus des bases du rhomboèdre.

Le plan ACA'C' normal aux faces ABCD et A'B'C'D' dans lequel les images ordinaires et extraordinaires du trait semblent se superposer sera le plan de section principale. Le cristal que nous utilisons est un rhomboèdre régulier que l'on peut considérer comme un cube qui été aplati suivant la diagonale AA'. En A comme en A' les angles des trois faces correspondantes sont égaux et ont pour valeur 101°53'. La diagonale AA' est un axe de symétrie d'ordre 3.

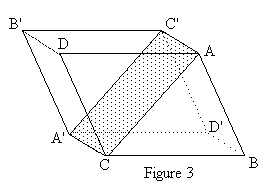
Les six faces parallèles deux à deux sont des losanges égaux. Sur la figure 3 le plan de section principale ACA'C' est représenté en grisé.

Dans ce plan, représenté sur la figure ci-contre, comme dans tout plan parallèle à celui-ci, un rayon incident normal à la face d'entrée se divise en deux rayons dont l'un suit un trajet ordinaire IJo et l'autre un trajet extraordinaire IJe.


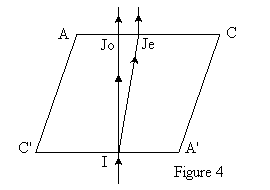
En posant le cristal sur la face ADB'C', c'est le plan ABA'B' qui serait plan de section principale.

Les deux plans ACA'C' et ABA'B' de même que le plan ADA'D' ont pour intersection la diagonale AA', qui sera par la suite la direction de l'axe optique

En 1690 le physicien hollandais Christiaan Huygens remanie et complète son "Treatise on Light" avec une étude des phénomènes de double réfraction.

" I attributed to this emanation of waves the regular refraction wich is observed in this stone, by supposing these waves to be ordinarily of spherical form, and having a slower progression within the Crystal than they have outside it."

"As to the other emanation whitch should produce the irregular refraction, I wished to try what Elliptical waves, or rather spheroidal waves would do..."

Il suppose que pour l'une des images observées à travers le cristal, les rayons suivent un trajet ordinaire (regular), obéissant aux lois normales de la réfraction avec des surfaces d'onde sphériques. Pour la seconde image, le trajet extraordinaire des rayons (irregular) n'obéit pas aux lois normales de la réfraction. Pour tracer ces rayons extraordinaires, il propose d'utiliser comme surfaces d'ondes des ellipsoïdes. Il découvre également que la double réfraction disparaît, lorsque les rayons réfractés dans le plan de section principale sont parallèles à la diagonale AA', qui sera la direction de l'axe optique du cristal. La méthode de construction des rayons réfractés qu'il propose est encore en usage actuellement. Ces déductions sont remarquables quand on sait, qu'à cette époque, en dehors de la lumière solaire, la seule source lumineuse était la bougie...
Construction d'Huygens des rayons réfractés                     

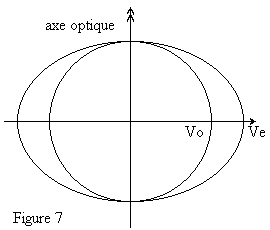A l'intérieur du cristal les surfaces d'onde ordinaire et extraordinaire sont construites en portant à partir d'une origine O, dans la direction de propagation du rayon, des longueurs respectivement proportionnelles a la célérité de l'onde ordinaire vo, et à la célérité de l'onde extraordinaire ve. Ces célérités sont égales lorsque la direction choisie est celle de l'axe optique. Dans le cas du spath qui est un cristal uniaxe négatif, la célérité v de l'onde extraordinaire atteint sa valeur maximale ve > vo lorsque la direction de propagation est normale à l'axe optique.

La surface d'onde extraordinaire est un ellipsoïde de révolution autour de l'axe optique qui enveloppe la nappe sphérique ordinaire.Nous avons représenté sur la figure ci-dessus la trace de cette surface d'onde dans un plan de section principale qui contient donc l'axe optique. L'équation de l'ellipse génératrice de la surface d'onde extraordinaire peut s'écrire:

Soit S la surface plane de séparation des deux milieux 1 et 2 (air - spath) et I un point de cette surface. Le plan de figure est un plan de section principale contenant l'axe optique et la normale à la face d'entrée.

  • Traçons dans le milieu 2 un cercle en pointillés de rayon ct, centré au point I qui représente la surface d'onde relative au milieu 1 à l'instant t. Le prolongement du rayon incident coupe ce cercle au point Q.
  • Menons par ce point la tangente au cercle qui coupe S au point I'. QI' représente la trace du plan d'onde du milieu 1 correspondant à l'incidence i l'instant t
  • Traçons également à l'instant t les surfaces d'onde d'origine I dans le milieu 2. Soit dans le plan de figure un cercle de rayon v t et une ellipse dont les demi axes ont pour longueurs vet et vot.
  • Menons à partir de I' la tangente en Qo au cercle de rayon vo t et la tangente en Qe à l'ellipse. I'Qo et I'Qe représentent respectivement à l'instant t , pour une incidence i, la trace des plans d'ondes ordinaire et extraordinaire dans le milieu 2.
  • Pour finir on construit les rayons ordinaire IRo et extraordinaire IRe . On remarquera que le rayon extraordinaire n'est pas normal au plan d'onde extraordinaire.
    Dans les triangles rectangles II'Q et II'Q nous avons:
    Le rayon ordinaire obéit aux lois de Descartes.

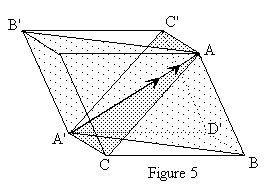
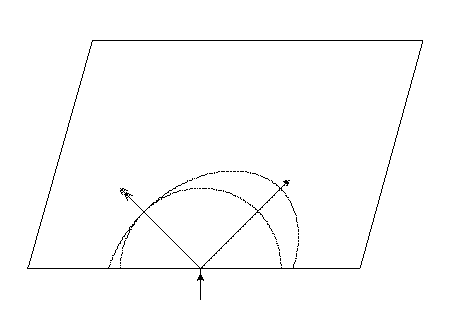A titre d'exercice, construisez sur votre feuille de résultats, les rayons réfractés dans le plan de section principale ACA'C' du cristal de spath.
En utilisant deux cristaux de spath d'Islande identiques successifs Huygens constate que si les faces en regard des deux cristaux sont orientées de la même façon on observe toujours deux images. Le trajet ordinaire des rayons dans le premier cristal reste ordinaire dans le second et de même pour le rayon extraordinaire. Par contre si le second cristal est orienté à 90° du premier, on observe toujours deux images mais par contre le rayon ordinaire du premier cristal devient extraordinaire dans le second et vice-versa pour l'autre rayon. Pour d'autres orientations on observe quatre images...

"But to tell how this occurs, I have hitherto found nothing whitch satifies me."

Isaac Newton dans son ouvrage "OPTICS" (1710) cite les travaux de Huygens qu'il nomme curieusement Hugenius, effectue semble-t'il les mêmes expérimentations sans donner d'explication satisfaisante. Au contraire il propose une théorie corpusculaire de la lumière manifestement fausse . Il démontre par exemple que la vitesse de la lumière est plus grande dans le verre que dans l'air. Cette théorie paralysera l'évolution des connaissances en optique pendant près d'un siècle.

EXPERIENCE & DÉCOUVERTE

Posez le deuxième cristal de spath d'Islande sur le premier et effectuez les mêmes observations que Huygens et Newton

 C'est en 1802 seulement, que le physicien et chimiste anglais William Hyde Wollaston vérifie expérimentalement la théorie d'Huygens . Avec des prismes de spath de même angle dans lesquels l'orientation de l'axe optique est connue comme ci-dessous et un goniomètre de son invention, il mesure l'indice extraordinaire n dans toutes les directions et retrouve la forme ellipsoïdale de la surface d'onde extraordinaire prévue par Huygens.

Le physicien français Louis Malus [Mem. Phys. Chim. Soc. D'Arceuil, 2, 143-158 (1809)]reprend également l'étude de la double réfraction.

" Si on reçoit un rayon de lumière perpendiculairement à la face d'un rhomboèdre de spath calcaire, ce rayon se divise en deux faisceaux, l'un qui se prolonge dans la direction du faisceau incident et l'autre qui fait avec celui-ci un angle de quelques degrés. Le plan qui passe par ces deux rayons jouit de propriétés particulières et on le nomme plan de section principale. "
Il découvre un phénomène nouveau.

" La lumière réfléchie par la surface de l'eau sous un angle de 52°.45' avec la verticale, a tous les caractères d'un des faisceaux produits par la double réfraction d'un cristal de spath calcaire dont la section principale seroit parallèle ou perpendiculaire au plan qui passe par le rayon incident et le rayon réfléchi que nous nommerons plan de réflexion. Si on reçoit ce rayon réfléchi sur un cristal quelconque, ayant la propriété de doubler les images, et dont la section principale soit parallèle au plan de réflexion, il ne sera pas divisé en deux faisceaux comme l'eût été un rayon de lumière directe, mais il sera réfracté tout entier suivant la loi ordinaire, comme si ce cristal avoit perdu la faculté de doubler les images. Si, au contraire, la section principale du cristal est perpendiculaire au plan de réflexion, le rayon réfléchi sera réfracté tout entier suivant la loi extraordinaire."

Pour des positions intermédiaires du cristal, il observe deux images (la flamme d'une bougie).

"En tournant le cristal autour du rayon visuel comme axe, on s'aperçoit qu'une des images s'affoiblit à mesure que l'autre augmente d'intensité... "

Si l'incidence de la lumière réfléchie sur la surface de l'eau est de 52° 45' l'extinction est totale. Il propose pour représenter la variation de l'intensité pour l'image ordinaire la loi :

où est l'angle entre le plan d'incidence et le plan de section principale

En 1811 le physicien écossais David Brewster reprend les expériences de polarisation par réflexion de Malus et remarque que la tangente de l'angle obtenu par Malus est égale à l'indice de réfraction de l'eau.

tan 52°45' = 1, 315 ( n =1,33 à 20°C )

Il montre que la loi reste valable pour la réflexion sur la surface de nombreux autres milieux transparents pour lesquels on pourra donc prévoir l'incidence i pour laquelle B la polarisation est totale en calculant: iB = atan n incidence de Brewster.Signalons également que Brewster a découvert la biréfringence mécanique en 1815 et aussi l'inventeur du kaleidoscope

En 1811 François Arago découvre la polarisation rotatoire du quartz. Membre de l'académie des Sciences, il parraine les travaux de Fresnel, qui publie en 1815 un premier mémoire sur les phénomènes d'interférences et 1819 sur la diffraction . La théorie ondulatoire donne des résultats satisfaisants, mais la nature de la vibration lumineuse reste inconnue.

Huygens supposait la vibration lumineuse longitudinale, mais les expériences effectuées avec les cristaux biréfringents suggèrent plutôt une vibration transversale.

Pour vérifier cette hypothèse Fresnel et Arago effectuent une expérience d'interférences à deux sources en lumière polarisée comparable à celle proposée ci-dessous . Les polariseurs sont des lames de tourmaline taillées parallèlement à l'axe optique.

Ces cristaux biréfringents dichroïques présentent la propriété d'absorber très fortement la vibration ordinaire ne laissant passer que la vibration extraordinaire

Dispositif des bilentilles de Billet
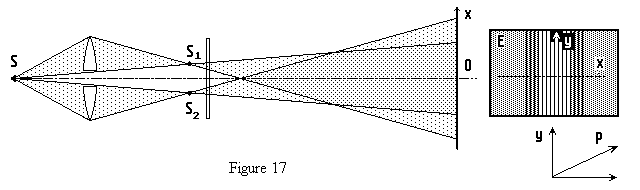Une lame polarisante P est placée derrière les sources images S1 et S2 . Les interférences subsistent, la frange centrale est brillante . Une rotation de la lame P dans son plan ne change rien.
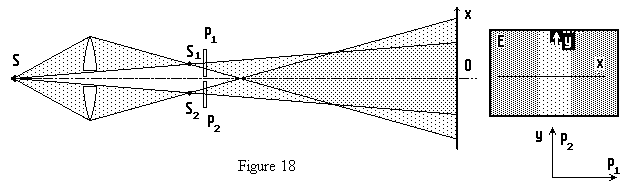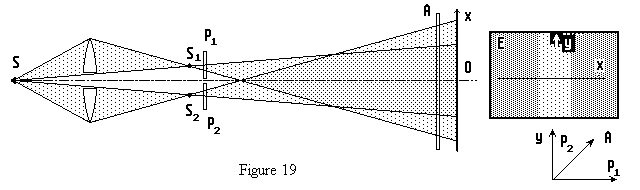
La lame P est coupée en deux morceaux P1 et P2 . P1 est placée devant S1 et P2 devant S2, mais P a été tournée de 90° dans son plan (cf. schéma). Les franges d'interférences disparaissent, l'éclairement de l'écran est uniforme.

Ce résultat est facile à démontrer si la vibration lumineuse peut être représentée par un vecteur transversal. Additionnons au point M de l'écran deux vibrations vectorielles monochromatiques et isochrones.

La vibration résultante au point M sera :

L'énergie de la vibration résultante est proportionnelle au carré de l'amplitude :

L'intensité est fonction de la phase. On observe des interférences

L'éclairement est uniforme.

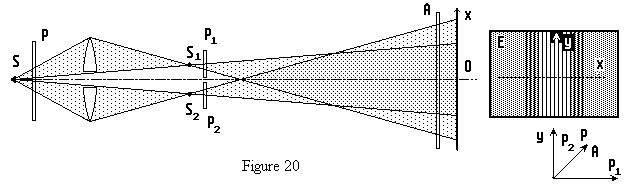
Après avoir repéré les directions donnant une extinction soit avec P1 soit avec P2 , on oriente à 45° de ces directions une lame analyseur A placée juste devant l'écran. Les vibrations issues de P1 et P2 après projection sur la direction A comme l'indique la loi de Malus sont parallèles. Mais l'éclairement de l'écran reste uniforme dans la zone de recouvrement des faisceaux. ? ? ?
Une lame polariseur P orientée comme A est placée juste devant la source ponctuelle. La figure d'interférence est de nouveau visible et la frange centrale repérée en lumière blanche est brillante.
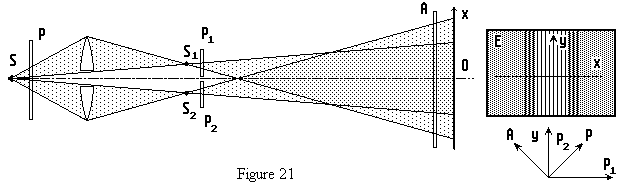Si A est perpendiculaire à P, on observe encore, des franges mais le contraste est inversé, la frange centrale est sombre.

Ainsi s'explique le résultat négatif de la troisième manipulation. En lumière naturelle, en l'absence de P, l'orientation de la vibration incidente émise par trains d'ondes très brefs est aléatoire. Même si des vibrations parallèles s'additionnent au point M de l'écran, statistiquement l'éclairement est uniforme pour l'observateur.

Cette expérience démontrait définitivement le caractère transversal de la vibration lumineuse que Fresnel représentera ensuite par un vecteur.


En 1815 le physicien français Jean-Baptiste Biot montre que certains liquides traversés par un faisceau de lumière polarisée produisent comme le quartz lorsqu'il est traversé parallèlement à l'axe optique une rotation de la vibration lumineuse. C'est la polarisation rotatoire.

Biot montre qu'il existe des substances levogyres qui font tourner le vecteur de Fresnel vers la gauche de l'observateur recevant la lumière et dextrogyres en sens inverse.

L'angle de rotation a est proportionnel à l'épaisseur de substance traversée, sensiblement inversement proportionnel au carré de la longueur d'onde et lorsqu'il s'agit solutions, proportionnel à la concentration.

Fresnel interprète la polarisation rotatoire par la biréfringence circulaire. A l'intérieur de la substance active la vibration incidente est décomposée en deux vibrations circulaires droite et gauche qui se propagent à des vitesses différentes et donnent en sortie une nouvelle vibration rectiligne dont le plan de polarisation a tourné d'un angle a proportionnel à la biréfringence circulaire nd- ng .

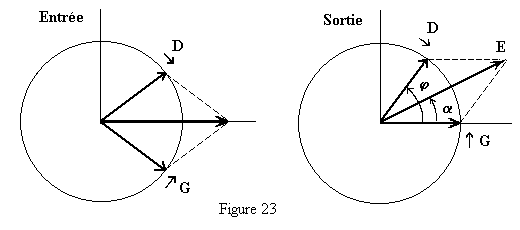A la sortie, la vibration circulaire droite D est en retard de :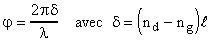

La vibration résultante à tourné d'un angle :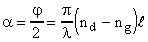
En 1828 William Nicol fabrique ses premiers polariseurs. Il scie un rhomboèdre de spath perpendiculairement à un plan de section principale et après polissage et ajustement des faces recolle les deux morceaux avec du baume du Canada (une résine de sapin) dont l'indice est voisin de 1,55, intermédiaire entre les indices ordinaire (no = 1,66 ) et extraordinaire (ne =1,49) du spath.

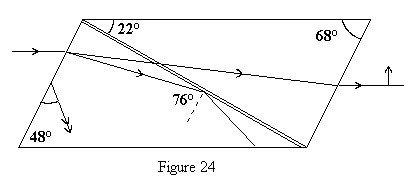
La figure 24 montre le trajet d'un rayon dans un plan de section principale. Le rayon ordinaire subit une réflexion totale en I. Seul le rayon extraordinaire traverse le Nicol dont un exemplaire sera disponible en salle de travaux pratiques.
En 1846 Michaël Faraday découvre le phénomène de polarisation rotatoire magnétique. Un liquide ou un solide traversé par un faisceau de lumière polarisée produit une rotation du plan de polarisation s'il est soumis à un champ magnétique parallèle à la direction de propagation. L'angle de rotation est proportionnel au champ magnétique appliqué.

En 1875 Le physicien écossais John Kerr découvre que certains liquides transparents comme le nitrobenzène deviennent biréfringents si un champ électrique est appliqué perpendiculairement à la direction de propagation de la lumière. L'axe optique est parallèle au champ électrique et la biréfringence provoquée est proportionnelle au carré du champ électrique.
En 1870 James Clerk Maxwell observe que certains liquides en écoulement à vitesse constante deviennent biréfringents.

En 1876  il publie sa théorie des ondes électromagnétiques et considère la lumière comme une onde électromagnétique de très haute fréquence (qcq 1014 Hz).

Sa théorie permet de retrouver les lois de la réfraction de la réflexion, la propagation dans les milieux isotropes et anisotropes et la forme des surfaces d'ondes dans ces milieux.

En 1890 Wiener parvient à enregistrer photographiquement des ondes stationnaires obtenues en éclairant sous incidence normale un miroir métallique avec un faisceau de lumière monochromatique parallèle. Son dispositif est en quelque sorte un coin d'air dont la glace inférieure a été argentée tandis que la face en regard de la glace supérieure est recouverte d'une très fine couche de collodion au bromure d'argent. L'amplitude de l'onde réfléchie étant pratiquement égale à celle de l'onde incidente, ce sont effectivement des ondes stationnaires qui ont enregistrées. Les résultats montrent qu'il existe une zone nodale au niveau de la surface du miroir. C'est donc le champ électrique qui représentera, dans le vide ou dans l'air, le vecteur de Fresnel.

Par ailleurs les expériences de polarisation par réflexion sur une substance transparente sous incidence de Brewster montrent que la vibration réfléchie est perpendiculaire au plan d'incidence. Il sera facile d'en déduire que dans les cristaux biréfringents la vibration ordinaire est perpendiculaire au plan de section principale et que la vibration extraordinaire est située dans le plan de section principale. Nous avons d'ailleurs représenté ces vecteurs dans les constructions d'Huygens des rayons réfractés.

Dans les milieux anisotropes la théorie de Maxwell montre que c'est le vecteur excitation électrique D qui représente le vecteur de Fresnel (cours).

En 1896 A. Cotton et H. Mouton découvrent la biréfringence du nitrobenzène soumis à un champ magnétique transversal intense. L'effet est proportionnel au carré du champ magnétique appliqué.

Les cours d'optique ondulatoire modernes débutent généralement par un rappel des équations de Maxwell et présentent l'optique ondulatoire comme un résultat des théories de Maxwell. C'est oublier un peu le long et passionnant cheminement expérimental de ses prédécesseurs qui lui ont permis de présenter une théorie si bien construite.

Ici se termine ce long prologue historique. Aujourd'hui la plupart des phénomènes de biréfringence ont reçu une explication théorique. Les applications sont multiples et très courantes comme par exemple l'affichage à cristaux liquides de vos calculatrices. Le cinéma en relief du futuroscope de Poitier est un autre exemple.

Polariseurs actuels et Films plastiques biréfringents

Les feuilles plastiques polarisantes actuellement utilisées pour remplacer les nicols ou les lames de tourmaline font l'objet de secrets de fabrication. Le nom polaroïds habituellement utilisé pour les désigner est une marque déposée. On ne peut donner que quelques indications sur les procédés de fabrication.

Elles peuvent être constituées d'une suspension de très petits cristaux dichroïques dans une matière plastique transparente. Le laminage en feuilles oriente ces cristaux dans la même direction. La lumière transmise par celles-ci est fortement polarisée dans une seule direction.

Les polaroïds H sont constitués d'une feuille transparente d'alcool polyvinylique dont les molécules en longues chaînes sont alignées dans la même direction. La feuille a été imbibée d'une solution d'iode et séchée ensuite. La feuille polaroïd ainsi obtenue se comporte comme une grille constituée de fils microscopiques parallèles, analogue à celle utilisée pour les ondes électromagnétiques centimétriques et ne laisse passer que les ondes lumineuses orientées dans une direction privilégiée.

Les feuilles plastiques transparentes comme la cellophane obtenues par laminage sont fortement biréfringentes. Les orientations des vibrations transmises sont respectivement parallèles et perpendiculaires à la direction de laminage.

 Sommaire