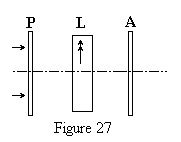
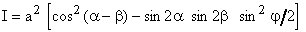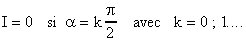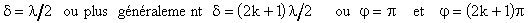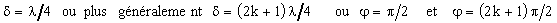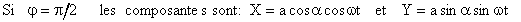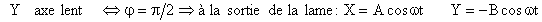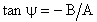Expérimentalement nous utiliserons essentiellement des lames découpées dans des feuilles plastiques transparentes qui tout en étant moins fragiles et moins coûteuses se comportent comme des lames cristallines à faces parallèles taillées parallèlement à l'axe optique d'un cristal uniaxe. 2.1 Vibration polarisée elliptique La lame cristalline L d'épaisseur e étudiée est intercalée entre la lame polariseur P et la lame analyseur A. Un faisceau de lumière monochromatique traverse le système sous incidence normale. Les axes représentant les directions privilégiées des vibrations sont Ox (horizontal) et Oy (vertical). A l'entrée de la lame la vibration incidente rectiligne P est décomposée en deux vibrations perpendiculaires Dx et Dy qui se propagent avec des célérités différentes vx et vy correspondant aux indices nx et ny . Sous incidence normale les vibrations suivent le même trajet. La différence de marche introduite est:
|
||
 |
Si comme dans le cas de figure ci-contre, l'axe optique est vertical et le cristal uniaxe positif (ne > no ; ve < vo) , Dx est la vibration extraordinaire et Dy la vibration ordinaire. Ox est l'axe rapide et Oy l'axe lent. A la sortie de L, les vibrations émergentes peuvent s'écrire |
|
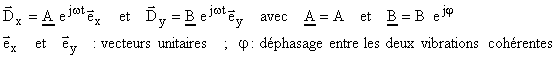
A la sortie de la lame la vibration résultante
sera : L'énergie de la vibration résultante est proportionnelle au carré de l'amplitude :
En l'absence d'analyseur l'éclairement sur un écran est uniforme. |
||
 |
En situant la vibration rectiligne incidente dans le premier quadrant,
la vibration émergente est elliptique et s'écrit en simplifiant:
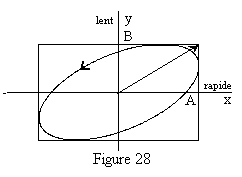
Le sens de parcours sur l'ellipse s'obtient en considérant que pour
t = 0 on a :
|
|
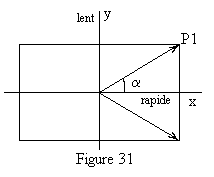
On en déduit que l'ellipse est décrite dans le
sens trigonométrique (vibration gauche ) pour
 et en sens
inverse pour 
( vibration droite ). |
||
 |
||
| 2.2 Intensité reçue à la sortie de
l'analyseur Soient  les
orientations respectives du polariseur et de l'analyseur par rapport aux
axes de la lame L. |
||
 |
A l'entrée de la lame appliquons la loi de Malus. La vibration
issue du polariseur P est projetée sur les axes de la lame et à
la sortie la vibration suivant l'axe Oy est retardée de
La vibration résultante transmise par l'analyseur est la somme de projections de Dx et Dy sur la direction privilégiée de l'analyseur A. |
|
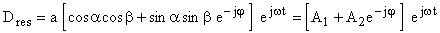
L'énergie de la vibration résultante est proportionnelle au carré de l'amplitude :
2.2.1 Détermination des axes de la lame Si le polariseur et l'analyseur sont croisés, la deuxième expression devient :
La méthode n'est pas utilisable si : 2.2.2 Lame demi-onde Le cas des lames demi-onde est plus important. La différence de marche introduite est :
entrée |
||
 |
Les vibrations Dx et Dy qui étaient en phase
à l'entrée sont en opposition à la sortie. Leur composition
donne encore une vibration rectiligne symétrique de la vibration incidente
par rapport aux lignes neutres. La "rotation" est de 2
On notera que les lames onde et demi-onde sont les seules qui attaquées par une lumière incidente rectiligne donnent une lumière émergente rectiligne, que l'on peut donc éteindre avec l'analyseur. |
|
| 2.1.3 Lame quart-onde _ Polariseur et analyseur circulaire
Ce type de lame introduit entre Dx et Dy une différence de marche :
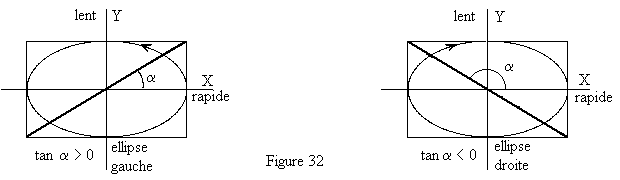
La vibration elliptique émergente a pour axes les lignes neutres de la lame.
Analysons quatre cas possibles suivant la disposition des axes de la lame
la vibration.
|
||
 |
||
 |
||
 |
||
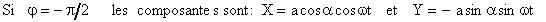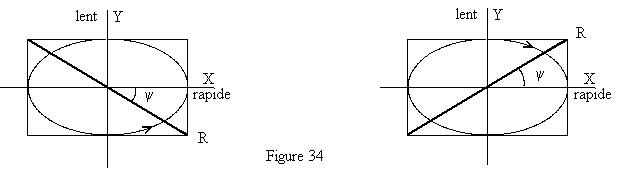
| On remarquera le sens de rotation sur l'ellipse est toujours
celui qui amène la vibration incidente P sur l'axe lent par une rotation
inférieure à 90°. Si  la vibration
émergente est circulaire. Un polariseur P suivi d'une lame
 dont les lignes
neutres sont orientées à 45° de P constitue un polariseur
circulaire. On utilisera la règle ci-dessus pour déterminer
si ce polariseur est circulaire droit ou gauche.
Un analyseur est sans action sur une lumière polarisée
circulairement non caractérisée par une direction
privilégiée mais seulement par un sens de rotation.
Interposons la lame
Le résultat est présenté sur la figure ci-dessous. La
direction de la vibration réctiligne rétablie est telle que :
|
||
 |
||
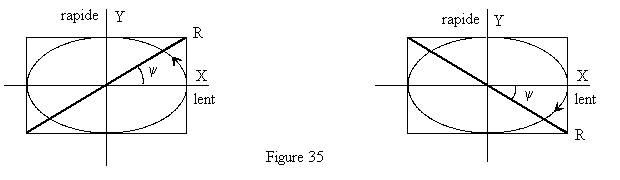
 Ici la direction de la vibration rectiligne rétablie est telle que :  |
||
 |
||
| La vibration rectiligne rétablie R est
située dans les quadrants tels qu'une rotation de 90° dans le
sens de la vibration elliptique incidente amènerait l'axe lent sur
l'axe rapide . Si la vibration incidente est circulaire, la lame  la transforme
en vibration rectiligne à 45° de ses lignes neutres quelle que
soit l'orientation de celles-ci. |
||
 |
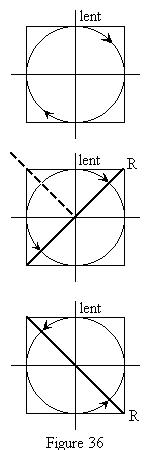Utilisons la règle que nous venons d'établir. Soit une vibration incidente circulaire droite reçue sur une lame  dont
l'axe lent est vertical et plaçons les flèches indiquant le
sens de rotation de la vibration dans les quadrants axe lent vers axe rapide.
La vibration rectiligne rétablie R est située dans ces quadrants et orientée à 45° des lignes neutres. La vibration rétablie R est éteinte par un analyseur dont la direction principale est située à 45° degrés des lignes neutres dans les quadrants opposés. Nous avons ainsi réalisé un analyseur circulaire droit. De tels analyseurs (ou polariseurs) circulaires sont réalisés simplement en collant une lame quart d'onde sur une feuille polaroïd. Un analyseur circulaire droit laisse passer totalement une vibration circulaire gauche quel que soit son azimut.
A titre d'exercice, vous indiquerez sur votre feuille de résultats
comment serait constitué un analyseur circulaire gauche. |
|
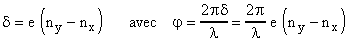
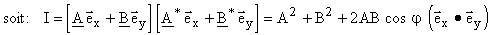
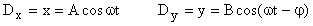
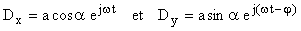
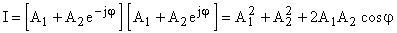
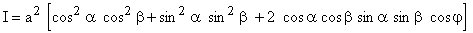
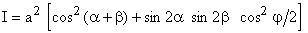où
La lame
est onde
sortie 
et de
transforme
une vibration elliptique en une vibration rectiligne si ses lignes neutres
sont parallèles aux axes de l'ellipse. En effet, les équations
paramétriques de l'ellipse rapportées à ses axes
sont:
avec ses axes
X et Y convenablement orientés :
