|
FACULTÉ DES SCIENCES ET DES TECHNIQUES DE NANTES |
|
Module de Physique Fondamentale Contrôle du 25/04/2001 Durée 2H |
Calculatrices autorisées cf. circulaire N°99-186 du 16-11-1999 MEN
Le matériel autorisé comprend toutes les calculatrices de
poche y compris les calculatrices programmables, alphanumériques ou à écran
graphique à condition que leur fonctionnement soit autonome et qu'il ne soit
pas fait usage d'imprimante. ….Le candidat n'utilise qu'une seule machine sur
la table….
Coin d'air et localisation des franges
Les figures inclues dans le texte ont été réalisées avec le logiciel cabri géomètre. Pour répondre à certaines questions vous devrez utiliser des intercalaires avec des figures à compléter.
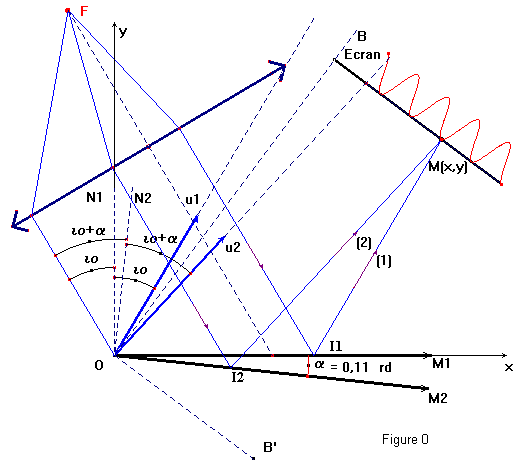
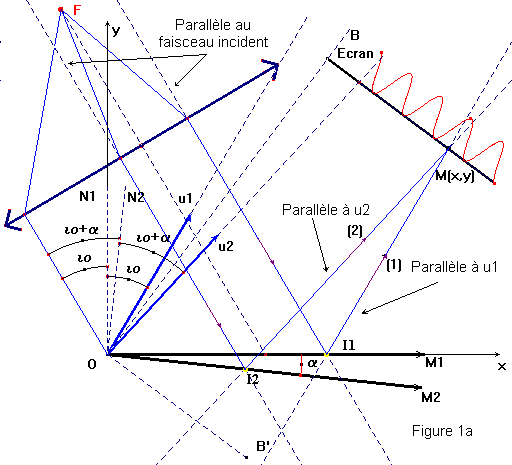
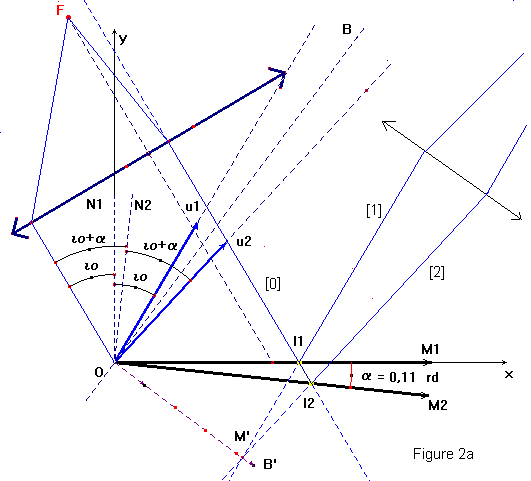
Soit un coin d'air d'angle α.. situé entre deux surfaces réfléchissantes M1 et M2. Le dispositif est éclairé latéralement sous l'incidence io. La droite d'intersection de ces deux surfaces est normale au plan de figure au point O origine du système d'axes xOy.
La source monochromatique de longueur d'onde λ est ponctuelle et située au foyer objet F d'une lentille convergente de distance focale f'.
Les vecteurs unitaires ![]() d'origine O
représentent les directions de propagation des ondes planes réfléchies par M1
et M2. Soient OB et OB'
respectivement les bissectrices intérieure et extérieure de l'angle des
vecteurs
d'origine O
représentent les directions de propagation des ondes planes réfléchies par M1
et M2. Soient OB et OB'
respectivement les bissectrices intérieure et extérieure de l'angle des
vecteurs ![]()
On a placé
perpendiculairement à la direction moyenne des faisceaux réfléchis, un écran
qui est donc parallèle à la seconde
bissectrice OB'. On supposera que les réflexions sont de même nature et
que les amplitudes des vibrations réfléchies sont égales. (A1=A2=A0).
1 Soit M (x,y) un point du plan de figure situé sur cet écran. On utilise pour cette question l'intercalaire 1 avec la figure 1
1.1 On observe sur cet écran des franges d'interférences, pourquoi? Expliquez vous simplement en quelques mots clés. Les franges sont elles localisées?
1.2 Exprimez
dans le repère xOy les composantes des vecteurs ![]()
1.3 Décrivez et montrez sur le schéma, les étapes de la construction des rayons [1] et [2] qui vont de la source au point M de l'écran.
1.4 Au
point O, construisez les traces des plans d'onde P01 et P02 normaux aux
directions ![]() . Que dire de la différence de phase φ =φ2 –
φ1 et de la différence de marche δ au point
O?
. Que dire de la différence de phase φ =φ2 –
φ1 et de la différence de marche δ au point
O?
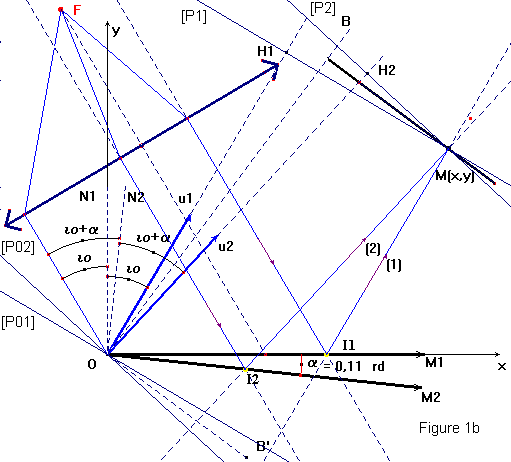
1.5 Au
point M construisez les traces des plans d'onde [P1] et [P2] normaux aux
directions ![]() et les projetés orthogonaux
H1 et H2 de M sur ces directions
et les projetés orthogonaux
H1 et H2 de M sur ces directions
Que dire de la différence de marche δ0 et de la différence de
phase φ0=φ2 – φ1 au
point M?
1.6 Exprimez δ0(M) et φ0(M) en fonction de x,y, io+α, α et si nécessaire de λ.
1.7 Déterminez l'intensité I(M) au point M en fonction de A0 et de φ0.
1.8 Déterminer en fonction de x,y, io+α, α, λ et de k, l'équation y=f(x) des courbes qui représentent dans le plan de figure la trace des surfaces où l'intensité est maximale. Tracez ces courbes sur votre figure 1. (intersections avec l'écran et OB')
1.9 Décrire l'aspect des franges sur l'écran et déterminez l'interfrange itf en fonction de α et de λ
2 On considère maintenant un écran "virtuel" dont la trace dans le plan de figure serait celle de la seconde bissectrice OB'. Soit M'(x,y) ou M'(ρ,θ) un point de cet écran virtuel.
2.1 Construisez le rayon [2] réfléchi sur M2 qui semble provenir du point M' puis le rayon [0] en provenance de la source. Montrez que la construction du rayon [1] semblant provenir du point M' est ensuite très simple.
2.2 Quelle particularité importante présentent les rayons réfléchis [1] et [2] qui semblent provenir de M'?
2.3 Décrire brièvement ce que devrait voir l'observateur qui accommode sur le plan OB'. Quelle est la valeur de l'interfrange (sur OB'). Représenter les maxima d'intensité par des points sur OB'. On notera ρk la position de ces maxima
2.4 Un écran (réel) est placé perpendiculairement au faisceau réfléchi à une distance OE=1m. On dispose d'une lentille convergente de 8 dioptries. A quelle distance de l'écran doit on placer la lentille pour former une image nette de l'état interférentiel dans le plan OB'?
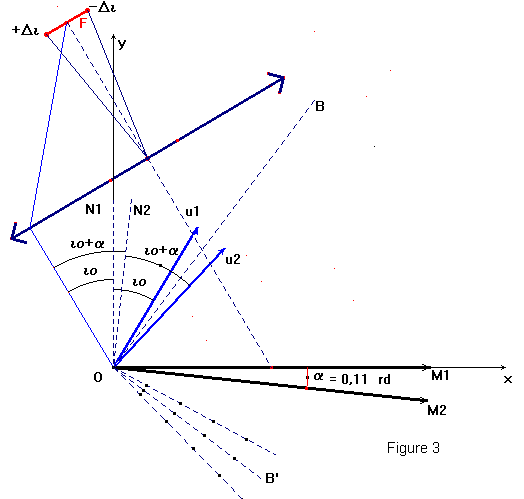
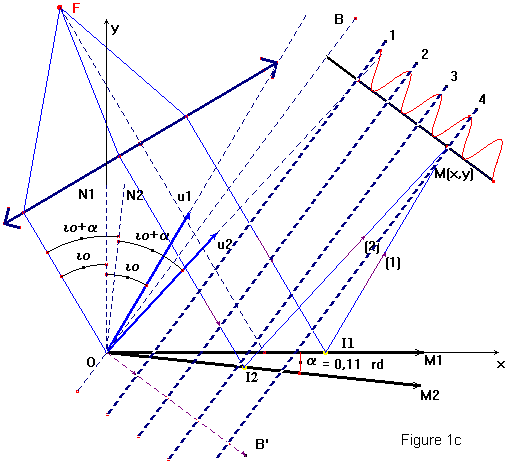
3 La source placée au foyer de la lentille de distance focale f'est une source large de largeur a. L'incidence du faisceau sur M1 variera donc de io-Δi à io+Δi. (intercalaire figure 3)
3.1 On
a représenté sur la figure 3 jointe en intercalaire, les positions extrêmes de
la seconde bissectrice des directions ![]() . Indiquez les valeurs correspondantes des angles
. Indiquez les valeurs correspondantes des angles
3.2 Les points représentés sur OB' correspondent à des maxima d'intensité. Pour les ordres 1, 2 ,3 et 4, représentez pour chaque position extrême (incidences io-Δi et io+Δi) la trace dans le plan de figure des surfaces d'intensité maximale (cf 1.8). Pour représenter la totalité de la source coloriez pour chaque ordre la zone intermédiaire entre deux positions extrêmes.
3.3 Pourriez vous observer des franges d'interférences sur l'écran de la première question? Quelle est selon vous la position la plus favorable pour l'observation de franges très contrastées? Quel adjectif qualifie les franges qui ne sont observables que dans une zone très limitée? Quel dispositif utiliseriez vous pour les montrer sur un écran?
3.4 Pour les ordres élevés, un brouillage des franges intervient même dans la zone très favorable définie ci dessus. En représentant plus précisément (Zoom sur la construction d'une une zone de contraste maximum) montrez que l'on peut évaluer simplement l'élargissement de la zone d'intensité maximale. Déterminer la valeur maximale de k, si on estime que le brouillage intervient quand l'élargissement atteint 1/4 d'interfrange.
4
Pour compléter la
démonstration géométrique
précédente on peut également chercher la zone de contraste maximum en
calculant l'intensité I(M) sous la
forme I(M) = Io [1+ V cos φ0].
On découpera la source large en sources élémentaires correspondant à
l'incidence io+i (i ![]() [- Δi , + Δi ]) et de largeur
angulaire di. On supposera que la contribution dI de la source à l'intensité
totale au point M est proportionnelle à di. On pourra donc procéder à calcul
d'intégration très approché qui a déjà fait ses preuves pour d'autres sources
larges.
[- Δi , + Δi ]) et de largeur
angulaire di. On supposera que la contribution dI de la source à l'intensité
totale au point M est proportionnelle à di. On pourra donc procéder à calcul
d'intégration très approché qui a déjà fait ses preuves pour d'autres sources
larges.
4.1 Pour la source correspondant à l'incidence io+i et de largeur angulaire di, déterminer la nouvelle expression de φ(M)
4.2 L'angle
i est assez petit pour que l'on puisse poser cos i ≈ 1 et sin i ≈
i. Exprimer φ(M) sous la forme
φ(M)= φ0+ φ(x,y,
i, i0+α, α, λ)
4.3 Exprimer
dI et intégrer l'expression de – Δi à + Δi. Présenter le
résultat sous la forme:
I(M) = Io [1+ V cos φ0].
4.4 Exprimer le contraste et montrer qu'il est maximum si le point M est sur OB'
4.5 De part et d'autre de OB', déterminez la position des surfaces sur lesquelles L contraste devient nul pour la première fois.
5 Le coin d'air traité dans ce problème peut être réalisé avec un interféromètre bien connu. Montrez schémas à l'appui comment vous pourriez reproduire les conditions expérimentales des questions 1, 2, 3
Rappels utiles
![]()
![]()
Bissectrice
extérieure (dans un triangle): Droite
passant par un sommet et perpendiculaire à la bissectrice intérieure
correspondante. 2 bissectrices extérieures et la 3e bissectrice
intérieure concourent en un point, centre d'un cercle exinscrit au triangle
(tangent à un côté et aux prolongements des deux autres).
Nom : prénom: Intercalaire N°

Nom : prénom: Intercalaire N°

2.1
Nom : prénom: Intercalaire N°
SOLUTION
Coin d'air et localisation des franges
1.1 La source est ponctuelle et monochromatique. Elle est placée au foyer F de la lentille convergente de distance focale f'. Une onde sphérique émise par la source devient une onde plane au delà de la lentille. Soit un plan d'onde P0,. tous les chemins optiques qui vont de la source à P0 sont égaux. Il en est de même pour les ondes réfléchies par les miroirs M1 et M2 qui sont cohérentes. On pourra donc toujours trouver au point M deux rayons cohérents issus de la source ponctuelle F.
1.2 Dans
le repère xOy les composantes des vecteurs ![]() sont:
sont:
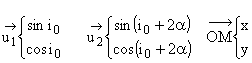
![]()
1.3 Pour
construire les rayons [1] et [2] on
trace par M deux parallèles aux directions
![]() . Les intersections avec M1 et M2 sont respectivement I1 et
I2 par lequels on mène deux parallèles à la direction i0. Soient J1
et J2 les points d'intersection avec la lentille. On trace ensuite en traits
pleins les segments FJ1 FJ2; J1 I1
J2I2 et I1M, I2M. On cache
ensuite les droites de construction.
. Les intersections avec M1 et M2 sont respectivement I1 et
I2 par lequels on mène deux parallèles à la direction i0. Soient J1
et J2 les points d'intersection avec la lentille. On trace ensuite en traits
pleins les segments FJ1 FJ2; J1 I1
J2I2 et I1M, I2M. On cache
ensuite les droites de construction.
1.4 Au point O on peut tracer les plans d'onde P00 (incident) P01 et P02.(réfléchis) Au point O φ = 0 et δ = 0
1.5 On
construit sur la figure les plans d'onde P1 et P2 passant
par M et les projetés orthogonaux H1 et H2 sur les
directions ![]() . En M et H1 la phase est φ1 pour l'onde plane
N°1 et φ2 en
M et H2 pour l'onde plane N°2. La différence de marche sera: δ0= OH2 –OH1
. En M et H1 la phase est φ1 pour l'onde plane
N°1 et φ2 en
M et H2 pour l'onde plane N°2. La différence de marche sera: δ0= OH2 –OH1
1.6 Dans
ces conditions:
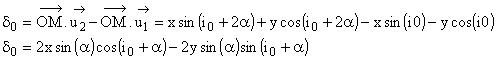
![]()
1.7 On
peut représenter les vibrations transversales qui parviennent au point M par:
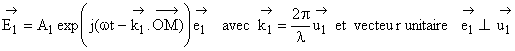
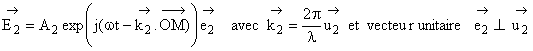
![]()
![]()
Au point M les vibrations sont cohérentes. Additionnons les vibrations:
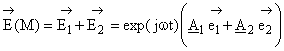
L'intensité détectée par le récepteur placé au point M sera proportionnelle au
carré de l'amplitude de la vibration résultante.

En tenant compte des données du texte: ![]()
1.8 L'intensité
est maximale si cos
φ0 = +1 ou si φ0
= 2 kπ
![]()
![]()
Ce sont des droites parallèles à la bissectrice OB de l'angle des
vecteurs ![]()
Elles coupent l'axe Ox en
![]() ou sur l'écran cf OB'
ou sur l'écran cf OB'
![]()
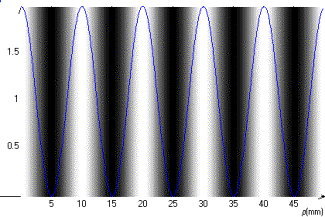
1.9 Les
franges brillantes sur l'écran sont rectilignes et parallèles à l'arête du coin
d'air. Elles apparaissent dans la zone de recouvrement des faisceaux issu de M1
et M2
Si O' est le point d'intersection de l'écran avec OB et ρ'=O'M on
aura :
![]()
2 On considère ,maintenant un écran virtuel placé selon OB'
2.1 On
trace par M' deux droites parallèles respectivement à ![]() qui coupent M1 en I1 et M2
en I2. En I1,construisons le rayon incident
correspondant. Dans le triangle MI1I2 0M' et OM1 sont bissectrices extérieures.
OM2 est donc bissectrice intérieure. Il en résulte que I1I2 est le prolongement
du rayon initial [0]
qui coupent M1 en I1 et M2
en I2. En I1,construisons le rayon incident
correspondant. Dans le triangle MI1I2 0M' et OM1 sont bissectrices extérieures.
OM2 est donc bissectrice intérieure. Il en résulte que I1I2 est le prolongement
du rayon initial [0]
2.2 Les rayons [1] et [2] peuvent ^être considérés comme résultants d'un même rayon initial. On parle dans ce cas de division d'amplitude.
2.3 Un
observateur qui accommode sur le plan OB' devrait voir des franges parallèles à
l'arète du coin d'air. Le calcul de la différence de marche est encore valable
![]()
2.4 Un
écran réel est placé à 1 m. la lentille est convergente et f'= 1/8= 0,125 m
Soit C le centre optique et A un point
du plan observé sur l'axe de la lentille et A' son image sur l'écran mous
aurons:
![]()
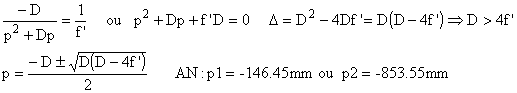
On choisira la première solution. Comme tout les chemins optiques qui vont d'un
point à son image sont égaux on obtiendra
sur l'écran une image nette et agrandie de l'état interférentiel dans le
plan de OB'.
3 On élargit la source. L'incidence variera donc de io-Δi à io+Δi
3.1 Les positions extrêmes de OB' seront donc io+α-Δi à io+α +Δi
3.2 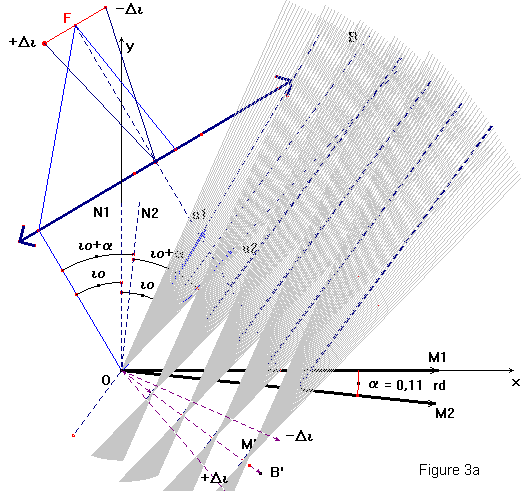 Télécharger
la figure Cabri
Télécharger
la figure Cabri
3.3 Sur l'écran de la première question on obtiendrait un éclairement uniforme. La zone la plus favorable pour l'observation des franges avec une source large est justement celle de l'écran virtuel de la deuxième question. On dit que les franges sont localisées. On les visualise en projetant l'image du plan de localisation OB' sur l'écran avec la lentille. Généralement on pose immédiatement que la seule solution pour obtenir des interférences localisées est la division d'amplitude et on détermine le la, différence de marche et le plan de localisation sans démontrer que c'est effectivement le plan d'observation le plus favorable.
3.4 Sur
la figure 4 on fait apparaître
l'élargissement PQ de la frange brillante d'ordre k.
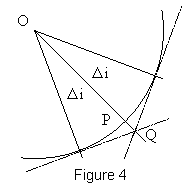
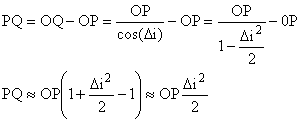
Pour évaluer le nombre des franges visibles nous estimerons que le brouillage
intervient si PQ > itf/4
![]()
![]()
![]()
4 Pour un calcul grossier on décompose la source en sources élémentaires de largeur angulaire di
4.1 La source élémentaire correspondant à
l'incidence i0+i
![]()
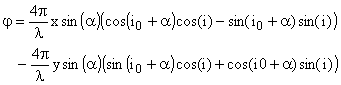
Utilisons les approximations proposées
![]()
![]()
4.2 L'intensité
correspondant à la source élémentaire sera donc:
![]()
![]()
![]()
![]()
![]()
![]()
4.3 Le
contraste est défini par:
![]()
donc C=V. Le contraste est maximum pour
![]()
Cette condition est remplie sur la droite :
![]()
C’est à dire sur la droite OB’ seconde bissectrice qui sera la trace du plan de localisation des franges sur le plan
de figure
4.4 Cherchons
la première annulation du contraste.
![]()
![]()
Ce sont donc deux droites parallèles à OB’ à une distance :
![]()
Si Di=5° on obtient
5,7 interfranges. On ne trouve pas de brouillage en s’éloignant sur OB’.
Avec des approximations plus fines en ce qui concerne le cos i. nous aurions
sans fait apparaître les termes correspondants au prix de calcul nettement plus
complexes. Cependant l’objectif de ce problème est atteint. Il nous sera
désormais plus facile d’admettre la localisation des franges avec une source
étendue. On retiendra que l’interfrange ne varie pas avec l’incidence et que la
surface de localisation est exactement celle que l’on retrouve en faisant
intervenir la division d’amplitude. "L'épaisseur" de la zone de
localisation est de deux ou trois interfranges. Dans le cas des anneaux de
Newton il sera inutile de se lancer dans des tracés complexes qui ne démontrent
rien, le plus simple suffira. On choisira une incidence normale entre lame et
lentille.
5 Pour cette question on se référera au texte du TP sur le Michelson
6 Texte et solution proposée par Jacques Charrier
 Télécharger
la figure Cabri
Télécharger
la figure Cabri