FACULTÉ DES SCIENCES ET DES TECHNIQUES DE NANTES

MAITRISE SCIENCES PHYSIQUES Module M1 de Physique

CIRCUIT RLC (Inspiré du Pb de CAPES 1988

En 1988 un élève nantais s'était classé Premier au CAPES et quatrième à l'agrégation de Physique

A-- Régime transitoire d'un circuit R,L,C.

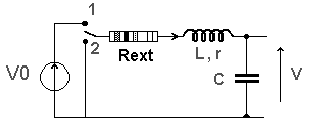Dans le circuit de la figure 1 Rext est la résistance d'un conducteur ohmique, L est l'inductance d'une bobine dont la résistance est r, C est la capacité d'un condensateur. On désigne par q(t) la charge instantanée du condensateur à la date t, i(t) l'intensité instantanée dans le circuit à la date t. On notera R la résistance totale du circuit.

A.1 -.En tenant compte des orientations indiquées sur le schéma, établir les relations entre q(t) et v(t) et entre q(t) et i(t) d'autre part.

A.2 On suppose d'abord que la résistance R est nulle. A l'instant t=0 on bascule l'interrupteur de la position 1 à la position 2. La tension initiale aux bornes du condensateur est v(0)=V0

Etablir l'équation différentielle à laquelle satisfait v(t); on posera : A.N:L=67mH ; C= 1 µF Calculer F0

A.3 On étudie le cas où la résistance R n'est pas nulle v(0)=V0

a) Etablir l'équation différentielle à laquelle satisfait V(t). On posera l=R/2L. A.N: Rext = 50 W, r = 27 W

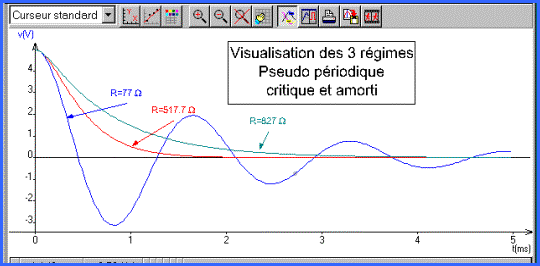
Déterminer les régimes d'évolution possibles pour la tension v(t)

b) Définir et exprimer la résistance critique Rc

A.4 On se place dans le cas où la résistance n'est pas nulle avec v(0)=V0

Calculer l'énergie dissipée par effet Joule au cours du régime transitoire. On représentera également l'énergie du condensateur et de la bobine

B-- Oscillations forcées d'un circuit R,L,C

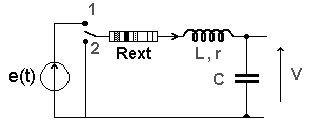On insére dans le circuit de la partie A un générateur de tension parfait cf figure 2 dont la tension instantanée aux bornes est: e(t)= em cos( wt + j) où em est la tension maximale; w la pulsation et j la phase de la tension par rapport à l'intensité.

B.1 Etablir l'équation différentielle à laquelle satisfait q(t)

B.2 Définir le régime transitoire et le régime forcé

B.3 En régime forcé on note l'intensité instantanée: i(t)=im cos wt

B.3.1 On introduit les grandeurs complexes associées à e(t) et i(t) soit respectivement:

Déterminer l'impédance complexe :

B.3.2 Exprimer im et j en fonction des caractéristiques du circuit (R, L,C) et de e(t)

B.3.3 On étudie la résonance

a) Q'appelle-t-on résonance en intensité?

b) quelle est alors la relation entre L,C et w?

c) Que peut on dire du circuit à la résonance

d) Donner l'allure de la courbe indiquant comment varie im en fonction de la pulsation w

e) Définir puis établir l'expression donnant la bande passante

f) Définir puis établir l'expression donnant le facteur de qualité

B.4 – En Régime Forcé , on note la tension aux bornes de l'inductance pure L :

B.4.1- Montrer que a peut se mettre sous la forme :

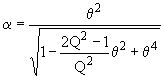
B.4.2 On étudie la variation de a

a) A quelle condition sur Q a admet-il un maximum

b) Calculez la valeur de qm correspondante en fonction de Q

c) Calculez la valeur a_m du maximum de a en fonction de qm

B.4.3 Etablir une expression équivalente simple de a quand q<<1. En déduire l’allure de la courbe a(q) au voisinage de l’origine.

B.4.4 Etablir une expression équivalente simple de a quand q>>1.Que peut on en déduire quant à la courbe représentative de a(q) ?

B4.5. A l’aide de développements limités d’ordre supérieurs au précédents, étudier comment suivant les valeurs de Q se situe la courbe a(q) par rapport aux courbes trouvées précédemment. (B.4.3 et B.4.4)

B.4.6 Sur le même système d’axes, donner les allures de courbes a(q) pour Q=0.5 et Q= 5

B.5 Calculer en régime forcé pour w=w_0 :

a) l’énergie dissipée en une période

b) l’énergie maximale W_L de la bobine.

c) L’énergie maximale W_C du condensateur

d) l’expression b= 2 p W_L/DW : que constate t’on ?

***

SOLUTION

A.1 On a bien entendu q(t)=C . v(t) et i= dq/dt = C dv/dt Il s'agit de définitions, établir n'est donc pas le mot juste.

A.2 R=0. L'application de la loi d'Ohm conduit à

L’équation différentielle sera résolue numériquement par Régressi sous la forme :

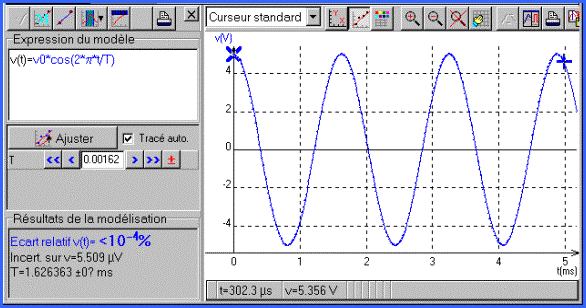
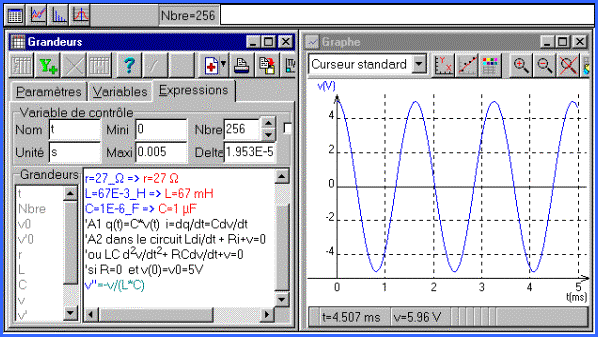Régressi trouve bien entendu une solution sinusoïdale avec les conditions initiales v(0)=v₀

En partant du modèle prédéfini on retrouve facilement a=0 ; b=v₀ j=0 soit v=v0 cos (2*p/T).

A.3 On étudie le cas où la résistance R n'est pas nulle v(0)=v0

a) Etablissons l'équation différentielle

Soit R=Rext +r . On crée la variable expérimentale Rext dans Régressi Rext= 50W

On pose et on calcule

L’équation différentielle sera résolue numériquement par Régressi sous la forme :

Régressi demandera les conditions initiales: v(0)= v₀ et v'₀=0 (courant nul)

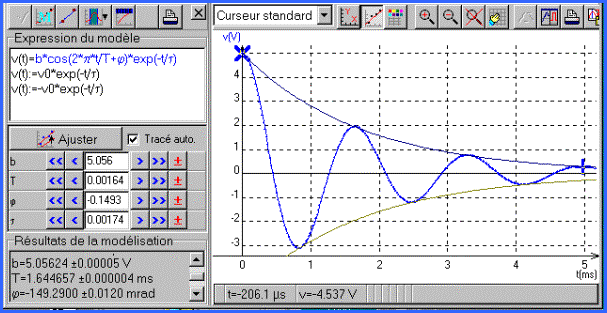
Lancez un calcul puis montrez puis modelisez les courbes obtenues pour v(t)

Solution analytique de l'équation différentielle

Résolvons l'équation différentielle:

L'équation caractéristique obtenue est:

Calculons la valeur numérique de D directement dans le page expressions de Régressi.

Le discriminant est négatif , les solutions s'écrivent donc:

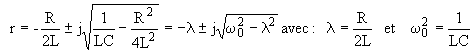
Une solution générale de l'équation différentielle est une combinaison de deux solutions particulières linéairement indépendantes:

Intercalez les lignes supplémentaires dans la page expressions de Régressi Windows

w=SQRT(wo^2-l^2)_rd.s-1 => w =3820 rd.s-1

vth=v0*EXP(-l*t)*(cos(w*t)+l/w*sin(w*t))

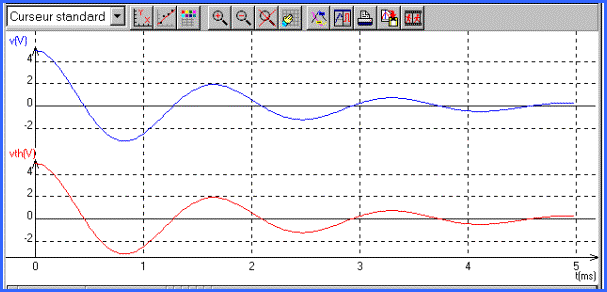
Les courbes v(t) en V et vth(t) en V se supperposent en mode normal ou sont identiques en présentation cf analyseur logique.

Si le discriminant D est nul l'équation caractéristique a une racine double: r = - l

est une solution particulière et on montre aisement que est une autre solution linéairement indépendante. La solution sera donc de la forme:

Si le discriminant est positif, l'équation caractéristique a deux racines réelles

A.4 Dans le cas où la résistance n'est pas nulle avec v(0)=v0

Calculons l'énergie dissipée par effet Joule au cours du régime transitoire.

Reprenons l'équation différentielle du circuit et multiplions les tensions par i pouir faire apparaître les puissances instanées. Multiplions ensuite par dt pour obtenir la variation élementaire d'énergie:

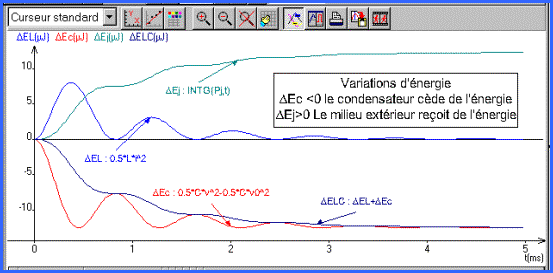
Il ne nous reste plus qu'a intégrer pour obtenir les variations d'énergie à l'instant t.

i varie de 0 à i et v de v₀ à v quand t varie de 0 à t.

Comme en fin de décharge i=0 et v=0 l'énergie dissipée est ½ Cv₀²

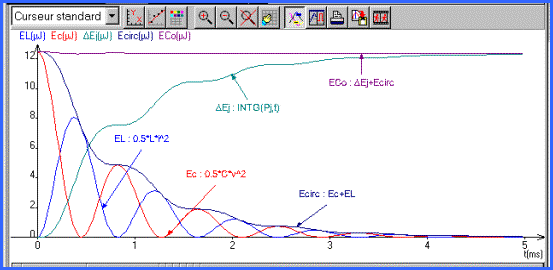
On a également coutume de représenter l'énergie contenue dans le condensateur

dans ce cas la démonstration est présentée ainsi:

On intègre en introduisant une constante E_C0

avec les conditions initiales choisies

B.1 Régime forcé. Etablissons l'équation différentielle

B2 Le régime transitoire intervient à la mise sous tension du circuit et il est représenté par la solution de l'équation différentielle avec second membre nul. C'est justement cette solution qui a été étudiée en A. la tension correspondante de vient rapidement nulle.

Si e(t) =em cos(wt+j) une fonction sinusoïdale de même pulsation est une solution particulière de l'équation avec second membre. Très rapidement cette solution est la seule à intervenir. Le générateur impose sa pulsation. Les oscillations sont forcées.

Pour visualiser proposons à Régressi de trouver la solution de l'équation différentielle

em= 5_V

E=em*cos(w*t)

On introduit le paramétre expérimental w et on lui donne une valeur proche de w₀ (3800°

v''=- 2lv' - w₀² v +  w₀² e

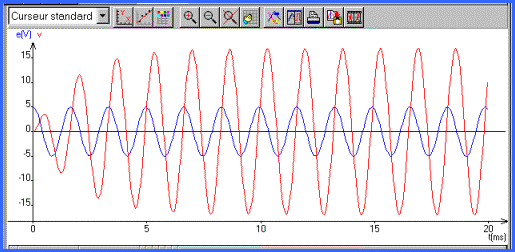
On observera la rapide installation du régime permanent. On utilisera l'animation pour faire varier w.

B.3 On préfère faire intervenir le courant dans l'équation différentielle.

B.3.1 Pour des calculs plus faciles on utilise de grandeurs complexes.

L'impédance complexe sera

B.3.2 i_m se déduit facilement de l'expression ci dessus:

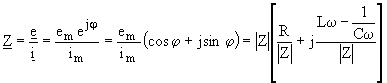
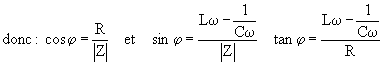
B.3.3a) La résonance en intensité correspond à une valeur maximale pour i_m

b)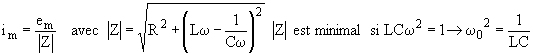

b) Ala résonance Z=R equiv une resistance pure et j=0

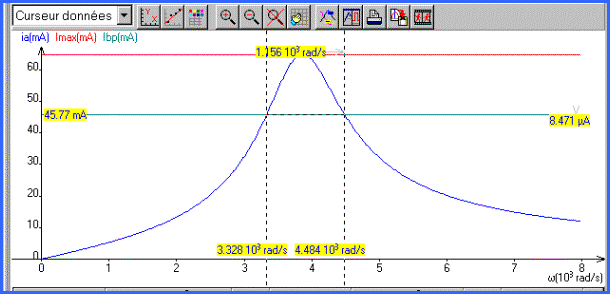
B.3.4 a) allure de la courbe im=f(w)

c) de part et d'autre du maximum, les extrémitès de bande passante sont atteintes lorsque la condition d'affaiblissement à 3 dB est remplie.

Soit

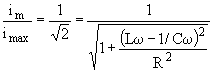
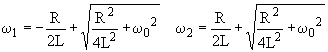
d) Le coefficient de qualité caractérise l'acuité de la résonance. L'une de ses définitions est :

B.4 Reprenons les données du texte :

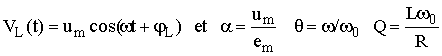
B4.1 en notation complexe :

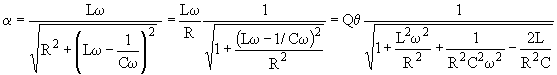
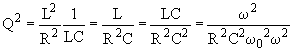
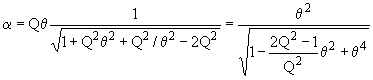
B.4.2 a) si le début de la courbe est parbolique

pour calculer la dérivée on peut mettre a sous la forme:

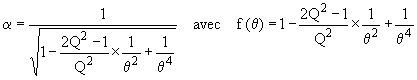
f'=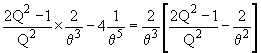

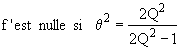on trouvera un maximum si 2Q²>1 ou

b la valeur de q_m correspondant au maximum s'il existe est:

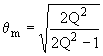
_c) Exprimons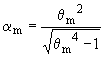

B.4.3 si q<<1 nous avons

B.4.4 si q>>1 on peut reprendre l'expression

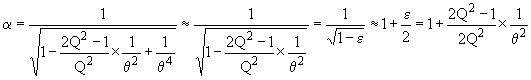
dans cette expression on retrouve la condition d'obtention d'un maximum

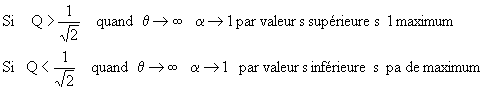
si q<<1 on peut reprendre l'expression

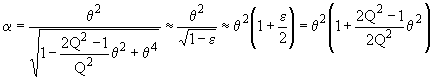
On retrouve si on se trouve au dessus de la parabole et au dessous si

B.4.6

B5 a)En régime forcé pour w = w₀ 0n a Z=R L'énergie consommée en une période sera

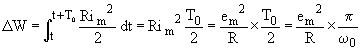
b) L'Energie maximale emmagasinée dans la bobine est:

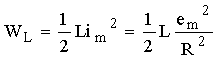
d) L'énergie maximale emmagasinée dans le condensateur est:

donc la même valeur que pour W_L

d) calculons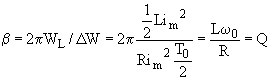

**********