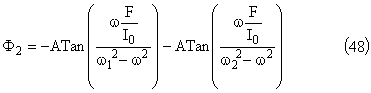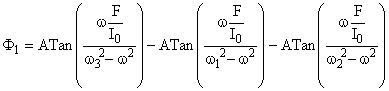FACULTÉ DES SCIENCES ET DES TECHNIQUES DE NANTES

LICENCE SCIENCES PHYSIQUES Module de Physique Fondamentale

OSCILLATEURS MECANIQUES à 1 ou 2

DEGRES DE LIBERTE

1 Introduction

Ce problème sera l'occasion de préparer la partie théorique d'un TP qui sera effectué au second semestre. Le texte de ce TP a été rénové. Vous utiliserez une notice hypertexte, une interface et un logiciel d'acquisition de données. Les résultats expérimentaux seront traités avec le logiciel Régressi. Dans ce problème nous utiliserons Régressi en mode simulation. Un ordinateur associé à un vidéo projecteur sera disponible en séance de Travaux dirigés.

2 Le pendule simple

Le dispositif expérimental du problème est une version simplifiée de celui que vous utiliserez en TP.

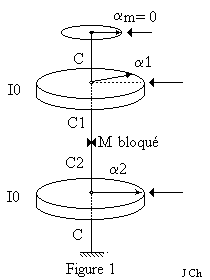Le dispositif comporte deux disques d'aluminium identiques D1 et D2 dont le moment d'inertie sera noté I0. Le disque supérieur D1 est suspendu par un fil de torsion vertical à un disque D0 auquel on peut imposer un mouvement de rotation sinusoïdal par l'intermédiaire d'un moteur, d'une came et d'une bielle non représentés sur la figure. La constante de torsion du fil  sera notée C.

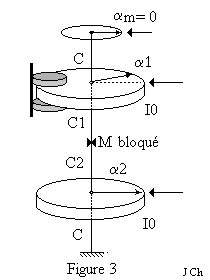
Le disque D2 est suspendu à D1 par deux fils de torsion placés bout à bout et de constantes de torsion C1 et C2. Un dernier fil de torsion vertical et de constante de torsion C relie le disque D2 au point de fixation inférieur.

On peut isoler les deux pendules en bloquant le point M, à la jonction des fils de constantes de torsion. C1 et C2 . Dans ce problème, nous poserons C=C1=C2, mais nous conserverons des notations différenciées compatibles avec celles utilisées dans le texte de TP.

Dans cette première partie le point M est bloqué. Le disque D0 est immobilisé (αm = 0 ). On étudie le mouvement du disque D1.

2.1 Déterminer le moment d'inerte I0 du disque D1 de rayon R, d'épaisseur e_D  et calculez sa valeur numérique.

A.N.:R =75E-3_m; r=2700_kg/m3 (Aluminium); eD =10E-3_m

2.2 Etablir l'équation différentielle du mouvement du disque D1.Dans la question 2 on notera α l'angle α1 pour alléger l'écriture et on posera Cp=C+C1

 Proposer une solution pour cette équation. On prendra pour conditions initales:

_rad/s

Le signe '(prime) signifie pour Régressi dérivée par rapport au temps (la variable de contrôle).

La dérivée seconde par rapport au temps sera notée  α'' (alpha prime prime).

On notera ω0 la pulsation propre du mouvement et T0 la période correspondante.

Pour les applications numériques on prendra C=C1= 20E-3_N.m/rad

Donner la solution analytique et proposez également à Régressi de trouver la solution numérique de l'équation différentielle.

Exprimer et calculer numériquement ω0 et T0

Avec Régressi on pourra obtenir la valeur de T0 en modélisant la solution numérique de l'équation différentielle

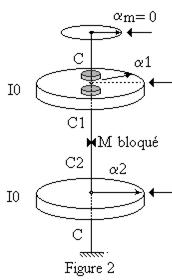2.3 On place symétriquement par rapport à l'axe de rotation deux surcharges sur le disque D1. Ce sont des petits cylindres d'aluminium de diamètre Φ et d'épaisseur h. la distance des axes de ces cylindres à l'axe de rotation sera noté r

Déterminer le moment d'inertie Is des surcharges par rapport à l'axe de rotation du pendule. Pour l'application numérique on prendra :

r = 0.055_m ; Φ = 0.0395_m; h = 0.017_m
2.4 Ecrire la nouvelle équation différentielle du mouvement. Avec les mêmes conditions initiales qu'en 2.2 déterminer la solution analytique et la solution numérique. Exprimer et calculer numériquement  la puslation propre ωs et la période Ts correspondante.

2.5 En TP, le moment d'inertie I0 et la constante Cp ne sont pas connues. Montrez que connaissant Is, il suffit de mesurer T0 et Ts pour déterminer I0 et Cp.

2.6 Quelles seraient respectivement les erreurs absolues ΔI0 et ΔCp de détermination de I0 et de Cp. Pour les applications numériques on prendra Δr= ΔΦ=Δh=0.0001_m.; Δρ=0 et ΔT0=ΔTs=0.001_s

2.7 Les surcharges sont retirées. Deux aimants permanents circulaires sont placés de part et d'autre du disque D1. Dès que le disque est en mouvement, des courants de Foucaults prennent naissance au sein du métal. Le moment  de freinage résultant ainsi obtenu est proportionnel à la vitesse de rotation du disque. On dit que le frottement est "visqueux" et le coefficient correspondant sera noté F.

Pour les applications numériques on prendra:
F=0.7 E^-3 m².kg.rad/s. (F=0.7 E-3_m2.kg.rad/s ds régressi)

Etablir la nouvelle équation différentielle  du mouvement  Avec les mêmes conditions initiales qu'en 2.2 et  sachant que le mouvement est oscillatoire amorti (F faible), déterminer la solution analytique et la solution numérique.

Déterminer et calculer numériquement la pulsation des oscillations amorties ωa, la période Ta correspondante et la constante de temps Tau  qui caractérise l'amortissement. On déterminera également ces mêmes valeurs en modélisant la solution numérique obtenue avec Régressi.

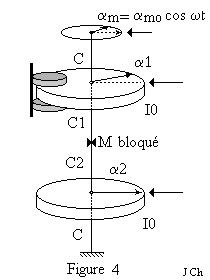
2.8 Le dispositif de freinage reste en place mais le moteur est mis en route à t = 0 et le mouvement du disque  D0 est de la forme αm = αm0 cos ωt.

Etablir la nouvelle équation différentielle du mouvement.

Déterminer la solution analytique et la solution numérique. Evaluer le temps nécessaire pour que le régime transitoire disparaisse.

Tracer avec Régressi Windows, les courbes α(t) sur un intervalle de temps de 20 s (1024 points) dans 16 pages successives pour les valeurs de ω données ci-dessous:

2.5; 3; 3.4; 3.8; 4.2; 4.6; 5; 5.2; 5.3; 5.4; 5.5; 5.6; 5.8; 6; 6.5; 7   rad/s

On prendra comme conditions initiales α_m0 = 0.1 rad et bien entendu α₀ = 0.05 rad et α'₀ =0

Observer sur les courbes successives l'établissement du régime permanent. Avec Régressi Windows il est possible de modéliser la portion régime permanent des courbes et d'obtenir dans chaque page l'amplitude et la période du régime permanent . (12<t<20 s)

2.9 En régime permanent les mouvements du disque et du moteurs seront de la forme:

ou encore en utilisant la notation complexe.

Déterminer le module α_P(ω) et l'argument ψ(ω ) de l'amplitude complexe α_P(ω ).

Montrez que vous pouvez retrouver la courbe correspondante en traçant le graphe paramètres des 16 pages calculées puis modélisées en 2.8

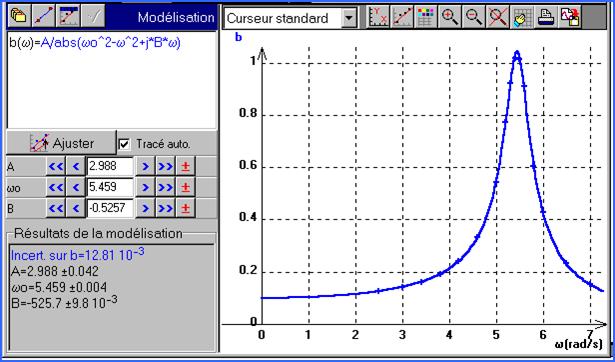
On modélisera la courbe avec :
b(ω)= A/abs(ωo^2-ω^2+j*B*ω)

Attention ωo et pas ω0  (oméga zéro déjà calculé) . La modélisation devrait réussir avec un peu d'aide (proposez ωo=5.5 et B=0.5)

3 Les pendules couplés

3.1 Pour l'étude des oscillations libres, le disque D0 est immobilisé sur la position α_m = 0. Déterminer la constante  de torsion Cs qui résulte de la mise "bout à bout" des fils de torsion C1 et C2.

Etablir les équations différentielles des mouvements α1(t) et α2(t).

Déterminer la pulsation ω3 du mouvement du pendule 1 lorsque D2 reste bloqué à sa position d'équilibre

Déterminer les pulsations propres ω1 et ω2 des mouvements sinusoïdaux qui constituent les solutions particulières du système d'équations différentielles.

Ecrire l'équation bicarrée et déterminer le coefficient de couplage K.

Résoudre numériquement les équations différentielles avec les conditions initiales suivantes:

 α10 = α20 = α0= 0,1 rad  et  α1'0 = α2'0 = 0 

α10 = -α20 = α0= 0,1 rad  et  α1'0 = α2'0 = 0
Proposer ensuite la solution la plus générale pour le mouvement des deux disques et déterminer analytiquement et numériquement la solution avec les conditions initiales suivantes :

α10 = α0= 0,1 rad         α20 = 0 et  α2'0 = α2'0  (vitesses initiales nulles)

Vérifier que vous pouvez par exemple modéliser la solution numérique avec la solution analytique. (c'est ce que vous ferez avec un enregistrement en TP)

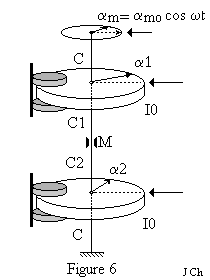
3.2 Pour les oscillations forcées on place les aimants sur chaque disque et le moteur démarre à l'instant initial :
 αm = αm0 cos ωt.

Etablir les nouvelles équations différentielles du mouvement.

Déterminer les solutions particulières puis la solution générale du système d'équations avec second membre nul. 0n posera :
θ = α1 + α2 et ψ = α1 - α2
et on supposera que le coefficient de frottement F est le même pour les deux disques: F=0.7 E-3_m2.kg.rad/s.

Proposer une solution particulière du mouvement avec second membre non nul. (pour l'équation 1) et donner enfin la solution générale.

Proposer à Régressi de résoudre numériquement ce système avec comme conditions initiales:

αm = αm0 = 0.1 rad ; α10 = 0.075 rad         α20 = 0.025 rad et  α2'0 = α2'0.

Le régime transitoire disparaît rapidement, seuls subsistent des mouvements sinusoïdaux de pulsation ω:

On utilisera la notation complexe; a₁(t)  a₂(t) et  a_m(t)  sont les parties réelles de :

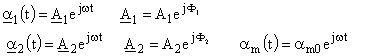
Déterminer les amplitudes complexes A₁ et A₂ dont on exprimera ensuite le module et l'argument. Tracer avec Régressi Windows les courbes correspondantes. Toutes les valeurs numériques nécessaires ont éte données ou calculées dans les questions précédentes.

SOLUTION

2.1 Calcul du moment d'inerte I0 du disque D1 de rayon R, d'épaisseur e_D .

Moment d'un disque ou cylindre par rapport à l'axe de révolution: I0=MR²/2

Démonstration rapide.

On découpe dans le disque un cylindre compris entre r et r.+ dr

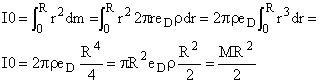
AN. dans Régressi Windows

I0=1.3419 10^-3 m².kg

2.2 Etablissons l'équation différentielle du mouvement du disque D1.Dans la question 2 on notera α l'angle α1 pour alléger l'écriture et on posera Cp=C+C1.

L’équation différentielle du mouvement est obtenue en appliquant le théorème du moment cinétique à l’instant t :

La solution générale est :

Proposer une solution pour cette équation. On prendra pour conditions initiales:

_rad/s

Dans la solution ci dessus nous aurons donc φ = 0

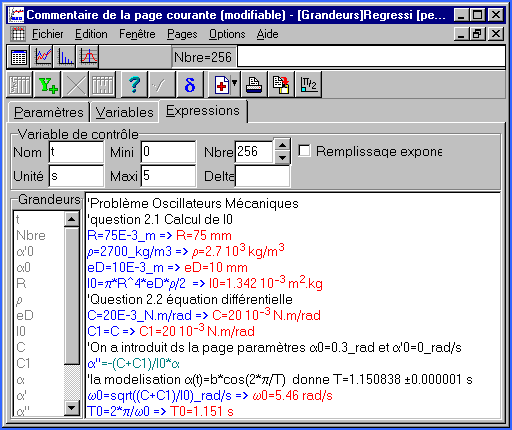
On écrira l'équation différentielle dans régressi à la suite du calcul de I0 sous la forme:

C=20E-3_N.m/rad

C1=C

α''=-(C+C1)/I0*α

Indiquer les conditions initiales et préciser les unités

Proposer un intervalle de temps de 5 s et 256 points pour le calcul

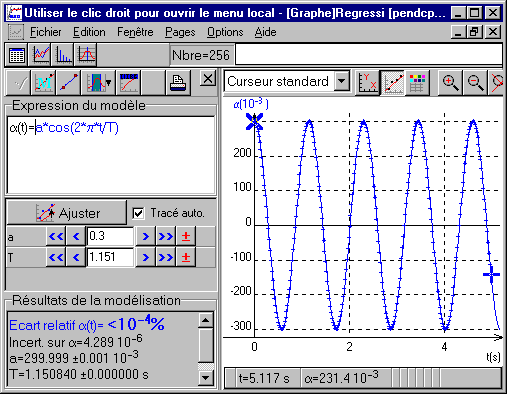
Afficher la page graphique et vérifier que vous pouvez modéliser la solution numérique avec avec la modélisation prédéfinie

α(t)=a+b*sin(2*π*t/T+φ) puis avec    α(t)=  b*cos(2*π*t/T)

On obtient: T=1.150839 ±0.000001 s

w0=sqrt((C+C1)/I0)_rad/s => w0=5.4597 rad/s

T0=2*p/w0 => T0=1.1508 s

2.3 On place symétriquement par rapport à l'axe de 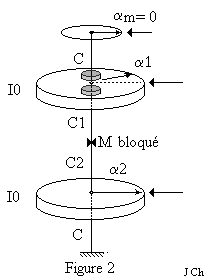rotation deux surcharges sur le disque D1. Ce sont des petits cylindres d'aluminium de diamètre Φ et d'épaisseur h. la distance des axes de ces cylindres à l'axe de rotation sera noté r

Déterminons le moment d'inertie Is des surcharges par rapport à l'axe de rotation du pendule.

Le moment d'inertie d'un petit cylindre par rapport à son axe sera:

On applique ensuite le théorème d'Huygens:

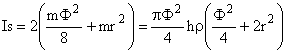
On effectue l'application numérique dans Régressi

r=0.055_m => r=55 mm

F=0.0395_m => F=39.5 mm

h=0.017_m  => h=17 mm

Is=p*F^2*h*r/4*(F^2/4+2*r^2) => Is=362.23 10^-6 m².kg

2.4 Ecrivons la nouvelle équation différentielle du mouvement.

Avec les mêmes conditions initiales la solution sera:

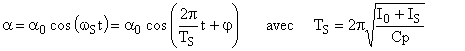
Dans Régressi, après avoir mis la première équation différentielle en commentaire.

  Question 2.4
a''=-(C+C1)/(I0+Is)*a

'la modélisation  a(t)=b*cos(2*p/T)  donne T=1.29690 ±0.00002 s

ws=sqrt((C+C1)/(I0+Is)_rad/s => ws=4.8448 rad/s

Ts=2*p/ws => Ts=1.2969 s

2.5 En TP, le moment d'inertie I0 et la constante Cp ne sont pas connues. Montrez que connaissant Is, il suffit de mesurer T0 et Ts pour déterminer I0 et Cp.

Avec les valeurs mesurées de T_S et de T₀ nous pourrons calculer I0 et Cp

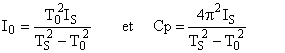
Dans Régressi Question 2.5
’I0 devient Io calculé avec Is T0 et Ts cf TP)

Io=T0^2*Is/(Ts^2-T0^2) => Io=1.3419 10^-3 m² .kg

Cp=4*p^2*Is/(Ts^2-T0^2)_N.m/rad => Cp=40 10^-3 N.m/rad

2.6 Quelles seraient respectivement les erreurs absolues ΔI0 et ΔCp de détermination de I0 et de Cp. Pour les applications numériques on prendra Δr= ΔΦ=Δh=0.0001_m.; Δρ=0 et ΔT0=ΔTs=0.001_s

Effectuons le calcul d'erreur sur Is

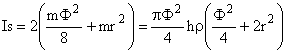
On rassemble les termes en dΦ (ici cela serait inutile car ils sont de même signe, mais …).

On remplace partout les "d" par des "Δ" en prenant la valeur absolue des termes correspondants.

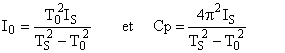
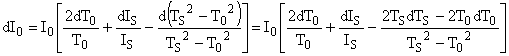
On rassemble les termes en dT₀ même s'ils sont de même signe

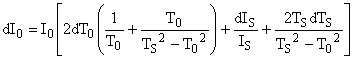
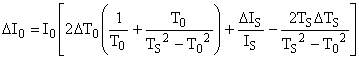
De même pour Cp:

Dans Régressi Windows

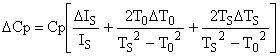
'Question 2.6 calculs d'erreur

Dr=0.0001_m => Dr=100 µm

DF=0.0001_m => DF=100 µm

Dh=0.0001_m => Dh=100 µm

DT0=0.001_s => DT0=1 ms

DTs=0.001_s => DTs=1 ms

DIs=Is*(2*DF/F+Dh/h+(F*DF/2+4*r*Dr)/(F^2/4+2*r^2)) => DIs=5.3 10^-6 m².kg

DI0=I0*(2*DT0/T0+DIs/Is+(2*Ts*DTs+2*T0*DT0)/(Ts^2-T0^2)) => DI0=40.10^-6 m².kg

DCp=Cp*(DIs/Is+(2*Ts*DTs+2*T0*DT0)/(Ts^2-T0^2))_N.m/rad => DCp=1.2 10^-3 N.m/rad

Le nombre de décimales dans les résultats de calculs d'erreur a été limité à 2. Vous ferez de même  en TP.

2.7 Les surcharges sont retirées. Deux aimants permanents circulaires sont placés de part et d'autre du disque D1.

On cherche des solutions de la forme:

La solution sera donc de la forme:

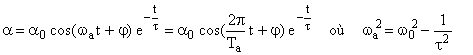
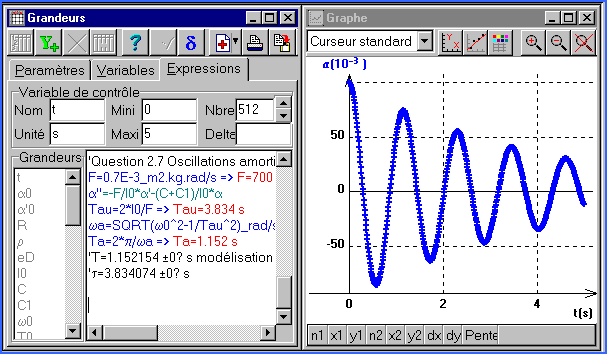
Question 2.7 Oscillations amorties

F=0.7E-3_m2.kg.rad/s => F=700 1e5  m .kg.rad/s

a''=-F/I0*a'-(C+C1)/I0*a

Tau=2*I0/F => Tau=3.8341 s

wa=SQRT(w0^2-1/Tau^2)_rad/s => wa=5.4534 rad/s

Ta=2*p/wa => Ta=1.1522 s

T=1.152154 ±0? s modélisation

t=3.834074 ±0? S

2.8 Le dispositif de freinage reste en place mais le moteur est mis en route à t = 0 et le mouvement du disque  D0 est de la forme αm = αm0 cos ωt.

 La nouvelle équation différentielle du mouvement.

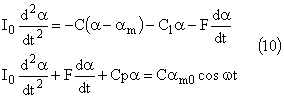
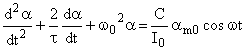
à la solution générale de l’équation avec second membre nul  s’ajoute une solution particulière de l’équation complète :

où w est imposée par le moteur. Le premier terme s’estompe progressivement.

Régressi

Question 2.8 oscillations forcées.

am0=0.1_rad => am0=100 mrad

ici déclarer un nouveau paramètre w

am=am0*cos(w*t)

a''=-F/I0*a'-(C+C1)/I0*a+C/I0*am

On trace les courbes demandées

Utilisons la notation complexe  puisque a(t)  et  a_m(t)  sont les parties réelles de :

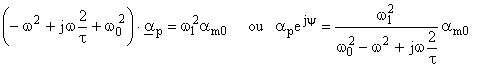
On en déduit l’amplitude a_p  et la phase y :

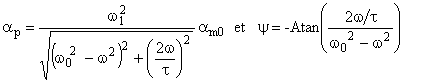
Avec la syntaxe de Régressi, nous écrirons (§ 2.2.5) la première expression sous la forme ::

ap=A/abs(w0^2-w^2+j*w*B)       abs(a+jb) signifie module du nombre complexe a+jb

Remarque: le maximum d'amplitude n'est pas obtenu exactement pour  ω = ω₀ mais pour une valeur un peu inférieure:

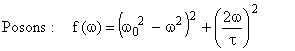
Amplitude et phase du mouvement forcé en fonction de la pulsation.

3 Les pendules couplés

3.1 Pour l'étude des oscillations libres, le disque D0 est immobilisé sur la position α_m = 0. Déterminer la constante  de torsion Cs qui résulte de la mise "bout à bout" des fils de torsion C1 et C2.

Etablir les équations différentielles des mouvements α1(t) et α2(t).

·

Les équations différentielles du mouvement sont obtenues en appliquant le théorème du moment cinétique à l’instant t :

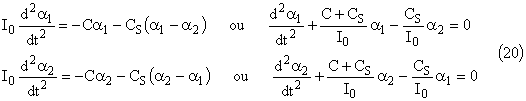
Si le pendule 2 est immobilisé, la première équation différentielle redevient celle d’un pendule simple:

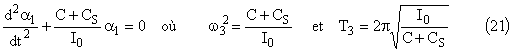
et de même pour le pendule 2 si on immobilise le pendule 1

Dans le cas général, les équations différentielles s’écrivent donc:

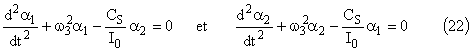
Une solution particulière convenant pour ce couple d'équations est une fonction sinusoïdale de même pulsation pour les deux mouvements. Soit en utilisant la notation complexe:

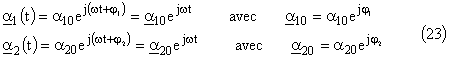
Notons aussi que α₁₀ et α₂₀ sont les amplitudes initiales demandées par Régressi pour la résolution numérique des équations différentielles.

Dans les équations différentielles nous obtenons:

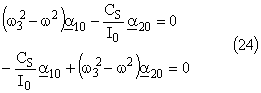
Le déterminant du système doit être nul:

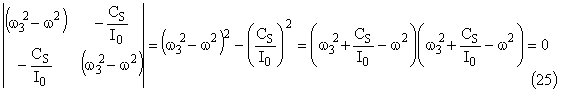
Les pulsations correspondant aux modes propres sont donc:

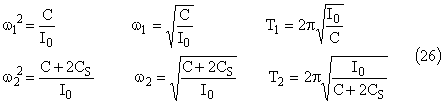
Nous pouvions également développer le déterminant sous la forme classique de l'équation bicarrée qui fait apparaître le coefficient de couplage K:

Les pulsations exprimées comme solutions de l'équation bicarrée s'écrivent aussi:

Reportons la valeur de ω₁ dans l'une ou l'autre des équations (24).

Nous obtenons: α₁₀ = α₂₀= A    les deux pendules oscillent en phase.

Pour obtenir ce type de mouvement il suffit donc d'écarter dans le même sens les deux pendules d'un même angle et de les lâcher simultanément sans vitesse initiale.

Reportons la valeur de ω₂ dans l'une ou l'autre des équations (24).

Nous obtenons: α₁₀ = - α₂₀     les deux pendules oscillent en opposition phase.

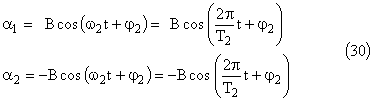
Pour obtenir ce type de mouvement il suffit donc d'écarter les deux pendules d'un même angle, mais en sens opposés et de les lâcher simultanément sans vitesse initiale.

Pour un mouvement plus général nous proposerons une combinaison linéaire des solutions particulières:

Prenons un exemple de mouvement avec battements qui sera testé en TP.

Le pendule 2 est maintenu à sa position de repos tandis que le pendule 1 est écarté d'un angle α₀. Les deux pendules sont ensuite libérés sans vitesse initiale à l'instant t=0

qui conduisent à:

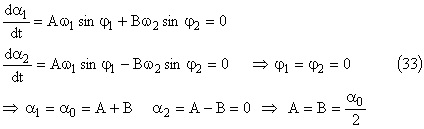
Le mouvement des pendules sera donc représenté par les équations suivantes:

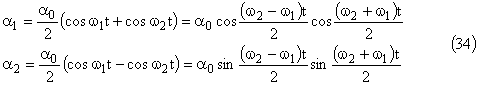
Nous obtenons des battements dont la pulsation de modulation sera notée ω_M

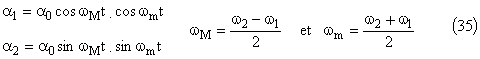
3.2 Le mouvement imposé par le moteur à l’extrémité du ressort de constante de torsion C sera de la forme :

L'équation différentielle pour le pendule 1 devient donc:

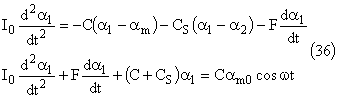
Ecrivons les deux équations différentielles:

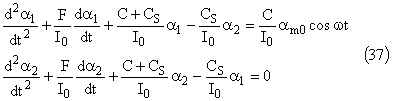
Lorsque le second membre de la première équation est nul on obtient le régime transitoire:

Posons θ = α_{1 +} α₂  et  ψ = α_{1 -} α₂

En additionnant puis en retranchant les équations différentielles:

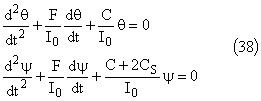
Comme en 2.1.3 , les équations différentielles peuvent s'écrire:

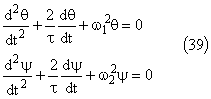
Comme l'amortissement est faible, les solutions sont:

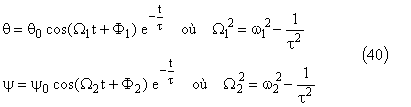
 En revenant aux variables initiales la solution générale de l'équation différentielle avec second membre nul sera::

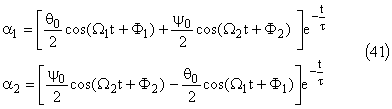
Après démarrage du moteur, le régime transitoire disparaît rapidement (t> 5τ), seuls subsistent des mouvements sinusoïdaux de pulsation ω:

Utilisons la notation complexe, a₁(t)  a₂(t) et  a_m(t)  sont les parties réelles de :

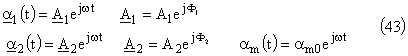
Dans les équations différentielles (37) nous obtenons :

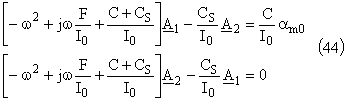
On obtient aisément l'amplitude complexe du mouvement du disque 2

Puis celles des deux  disques  

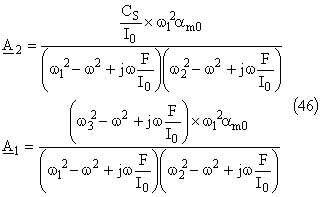
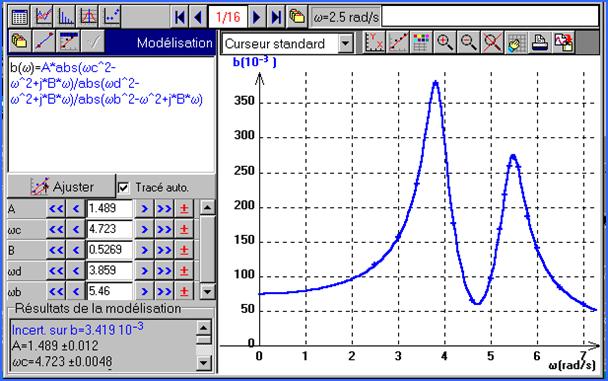
Exprimons les modules des amplitudes:

Comme dans le cas du pendule simple, les maxima et le minimum ne sont pas obtenus exactement pour  ω = ω₁ ; ω₂ ou  ω₃, mais pour des valeurs proches si l'amortissement est faible. Nous tracerons en TP la courbe expérimentale de l'amplitude A1 en fonction de la pulsation imposée. Les positions des maxima et du minimum ne seront que des indications pour aider Régressi Windows au cours de la modélisation.

Exprimons aussi la phase des mouvements: