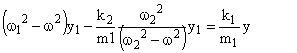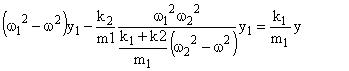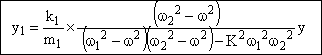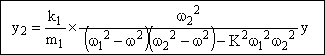|
|
LICENCE SCIENCES PHYSIQUES Module L1 de Physique
|
Pendules élastiques couplés et nombre d’or
On utilisera Régressi avec m=_0.1 kg et on choisira par exemple k pour obtenir T2=1_s
1 Une masse m1 est suspendue par un ressort
k1 à un point fixe O. Une deuxième masse m2 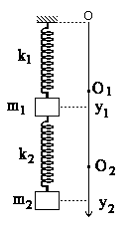 est
suspendue à m1 par un ressort k2. On ne considérera que
les mouvements de translation verticale des masses m1 et m2.
On appellera y1 et y2 les élongations des masses m1
et m2 par rapport à leur position quand le système est au repos.
est
suspendue à m1 par un ressort k2. On ne considérera que
les mouvements de translation verticale des masses m1 et m2.
On appellera y1 et y2 les élongations des masses m1
et m2 par rapport à leur position quand le système est au repos.
1.1 Déterminer les pulsations w1 des oscillations libres verticales de la masse m1 quand la masse m2 est immobilisée et w2 de la masse m2 quand la masse m1 est immobilisée.
1.2 Etablir les équations différentielles des mouvements des deux masses m1 et m2 quand le système est abandonné à lui même en dehors de son état d’équilibre.
1.3 En proposant des solutions sinusoïdales du temps de même fréquence pour y1(t) et y2(t), établir l’équation aux pulsations propres dans laquelle on fera apparaître le coefficient de couplage K2.
1.4 Montrez que l’équation aux pulsations propres a toujours des racines qui seront notées Wp et Wa ( Wp < Wa) dont on comparera les valeurs aux pulsations w1 et w2 en supposant par exemple w1 > w2.
1.5 Dans le cas particulier où k1=k2=k et m1= m2=m, exprimer les pulsations propres W et W’ et déterminer pour chaque mode le rapport des amplitudes des oscillations des deux masses m1 et m2. Proposer pour y1(t) la solution la plus générale du système d’équation différentielles (12) et en déduire l’expression de y2(t)
2 On impose à présent à l’extrémité supérieure du ressort de dureté k1 un mouvement sinusoïdal vertical y(t) = A cos wt autour de la position d’équilibre initiale O. Bien que l’amortissement puisse être considéré comme négligeable, on supposera qu’un régime permanent finit par s’établir.
2.1 Etablir pour ce régime les expressions de y1(t) et de y2(t) au cours du temps.
2.2 Etudier la variation de ces expressions en fonction de w. En particulier, pour quelles valeurs de w, les amplitudes des mouvements de m1 et m2 sont elles
a) maximales, b) minimales. A quelles conditions doivent satisfaire m1 m2 k1 et k2 pour que les minima d’amplitude de y1(t) et y2(t) se produisent pour la même valeur de ω
2.3 Etudier en fonction de ω, les relations de phase entre les mouvements de m1 de m2 et de l’extrémité supérieure O du ressort de raideur k1
Solution Pendules élastiques couplés
 1.1
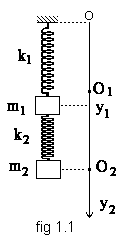
La masse m2 est immobilisée
1.1
La masse m2 est immobilisée
Soient l01 et l02 les longueurs des ressorts à vide.et l1 et l2 les longueurs à l’équilibre :
A l’équilibre :
![]()
![]()
Si m2 est immobilisée en 02 et m1 déplacée vers le bas (sens +) et en mouvement l’application de la relation fondamentale de la dynamique dans le repère du laboratoire supposé galiléen conduit à :
![]()
Compte tenu des relations à l’équilibre :
![]()
équation différentielle d’un
oscillateur harmonique dont la pulsation serait :
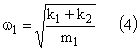
 M1
est immobilisée en O1 et M2 est en mouvement et située à la cote y2
L’application de la relation fondamentale de la dynamique conduit à :
M1
est immobilisée en O1 et M2 est en mouvement et située à la cote y2
L’application de la relation fondamentale de la dynamique conduit à :
![]()
Compte tenu de la relation (2)
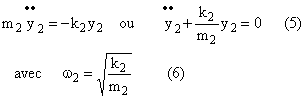
1.2 Les deux masses sont écartées verticalement hors de de leur position d’équilibre et sont en mouvement à l’instant t
Compte tenu des relations 1 et 2 nous ne considérons plus dans le bilan de force que les forces de rappel des ressorts correspondant aux allongements à par rapport aux positions à l’équilibre.
![]()
![]()
![]()
![]()
1.3 Ces équations différentielles couplées ont des solutions
particulières sinusoïdales de même pulsation ω cf :
![]()
en reportant dans (7) : ![]()
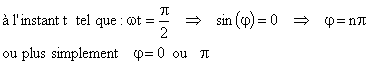
Les solutions particulières correspondent à des mouvements en phase ou en opposition de phase.
Dans (7) et (8) nous obtenons :
![]()
![]()
Ce système d’équations linéaires admet des solutions autres que le solution banale y1=y2=0 si le déterminant du système est nul, soit :
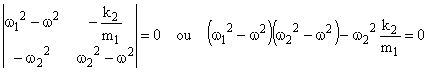
![]()
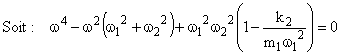
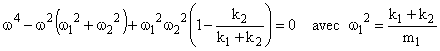
![]()
Cette expression est l’équation aux pulsations propres dans la quelle apparaît le coefficient de couplage K2 dont l’expression montre qu’elle que sa valeur est comprise entre 0 et 1
1.4 Pour résoudre l’équation bicarrée :
![]()
Calculons le discriminant : ![]()
Qui s’écrit encore : ![]()
L’équation 12 a donc toujours des racines réelles
Le produit des racines ( c/a)
=![]() > 0
=> racines de même signe
> 0
=> racines de même signe
La somme des racines (-b/a) = ![]() >
0 => Les racines sont positives
>
0 => Les racines sont positives
Dans ces conditions les pulsations propres sont :
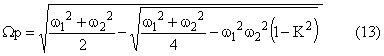
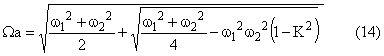
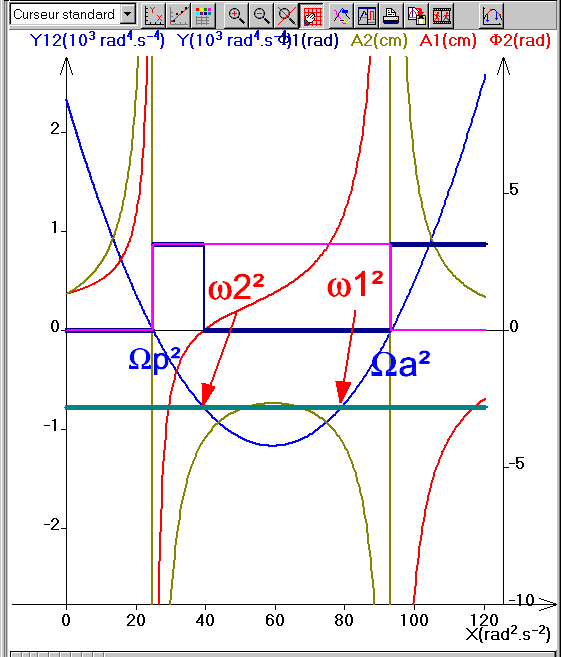
Pour comparer les valeurs de ces pulsations propres traçons la courbe Y(X) que nous pouvons écrire sous deux formes :
![]()
![]()
Traçons cette parabole avec Régressi avec m=0.1 kg T2= 1s et k1=k2=k
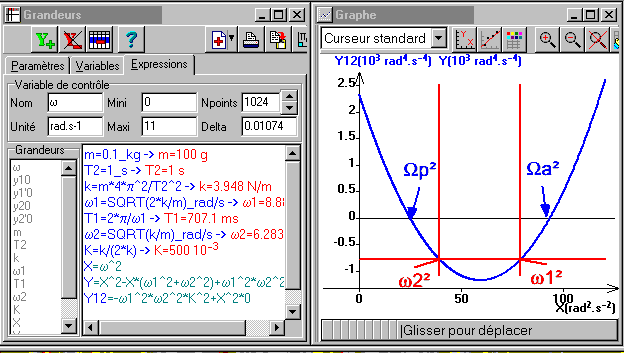
L’intersection de la parabole avec la droite horizontale Y12 permet de situer les pulsations ω1 et ω2 par rapport aux pulsations Ωp et Ωa
Reprenons les équations 9 et 10
![]()
si ω = Ωp y1 et y2 sont en phase et si ω = Ωa ils sont en opposition de phase
Si k1=k2=k et si m1=m2=m nous obtenons :
![]()
![]()
![]()
Où C est le nombre d’or
http://trucsmaths.free.fr/nombre_d_or.htm
Les pendules oscillent en phase et le rapport des amplitudes est le nombre d’or.
Construction du rectangle d’or avec Cabri Géomètre
![]()
![]()
Une combinaison linéaire des deux modes propres est une solution générale :
![]()
et compte tenu des relations ci dessus :
![]()
ou encore compte tenu des propriétés du nombre d’or
![]()
Dans ces conditions
particulières le système d’équations différentielles peut être résolu par Régressi.
Solution du système d’équations
différentielles
On testera le conditions initiale suivantes
y10= 0.1_mm et y20= 0.1618_m et y’10=y’20 = 0
y10= 0.1_mm et y20=- 0.0618_m et y’10=y’20 = 0
y10= 0.1_mm et y20= 0_m et y’10=y’20 = 0
y10= 0_mm et y20= 0.1_m et y’10=y’20 = 0
2 Ocillations forcées
Le support supérieur vibre de sorte que y = a cos ωt
Il faut donc maintenant tenir compte du mouvement du support dans la première équation différentielle.
![]()
![]()
Eliminons les termes inutiles
![]()
![]()
Bien que le terme d’amortissement ne figure pas dans nos équations on supposera qu’un régime permanent de pulsation ω finit par s’établir.
Dans ces conditions :
![]()