FACULTÉ DES SCIENCESET DES TECHNIQUES DE NANTES |
|
LICENCE SCIENCES PHYSIQUES Module L1 de Physique
|
Pendule élastique vertical (Inspiré du Pb de CAPES 1988)
En 1988 un élève nantais s'était classé Premier au CAPES et quatrième à l'agrégation de Physique
C Régime transitoire d’un oscillateur mécanique
On considère le dispositif de la figure ci-dessous.
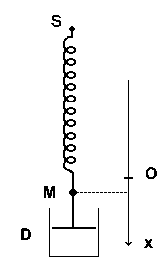
Un ressort élastique de masse
négligeable de raideur k, de longueur à vide l0 a son extrémité
supérieure S fixe. A l’extrémité inférieure est fixé un corps M assimilable à
un point matériel de masse m. Le rôle unique de l’amortisseur D, de masse
négligeable, lié à M est d’exercer sur le corps la force : ![]() désigne
la vitesse de M et h un coefficient de frottement fluide positif.
désigne
la vitesse de M et h un coefficient de frottement fluide positif.
Les mouvements de M sont verticaux ; ils sont étudiés dans le référentiel considéré comme galiléen pour lequel S est fixe. La position de M est repérée, au cours du temps, par son abscisse x(t) sur l’axe vertical descendant Ox. A l’équilibre l’abscisse de M est nulle.
C.1 A l’équilibre, l’allongement du ressort est désigné par a. Exprimer a en fonction de m de k et de la valeur absolue g de intensité de la pesanteur.
AN Régressi : m= 200 g ; a= 25 cm g=9.81 m/s² déterminer k (Unité ?)
C.2 Etablir l’équation différentielle du mouvement de M
C.3 On supprime l’amortisseur D, puis on abandonne M sans
vitesse initiale à l’abscisse x(0)=X0. Etablir l’expression de x(t) ;
on posera : ![]() AN Régressi : X0=10
cm
AN Régressi : X0=10
cm
C.4 Après avoir replacé
l’amortisseur D, on reprend la même opération que celle décrite précédemment en
C.3. On posera ![]() . (unité ?)
. (unité ?)
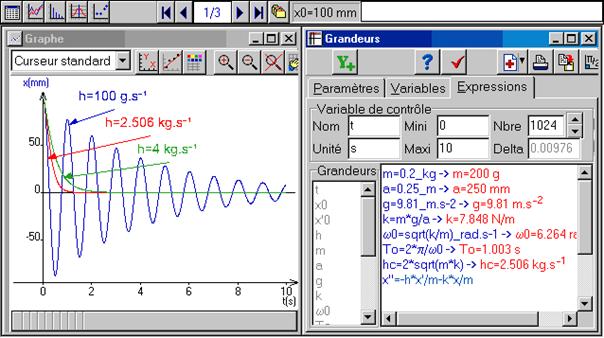
a) Déterminer explicitement les trois régimes possibles pour l’évolution de x(t). La résolution de l’équation différentielle est demandée.
b) Définir et exprimer le coefficient de frottement critique hc AN
c) Tracez avec Régressi trois courbes x(t) caractérisant les trois régimes
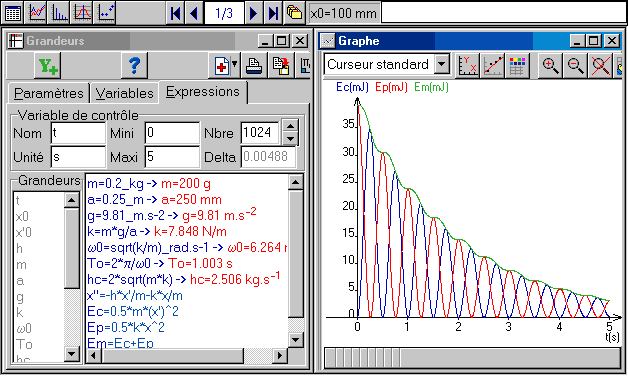
C.5 Tracez avec Régressi les 3 courbes représentant l’évolution de l’énergie cinétique potentielle et mécanique. Calculer l’énergie dissipée dans l’amortisseur pendant le régime transitoire.
D Oscillations forcées d’un oscillateur mécanique.
Au dispositif de la partie C, décrit à la figure 3, on ajoute, un dispositif supplémentaire grâce auquel le corps M est soumis à la force verticale f= fm cos wt qui vient s’ajouter aux forces étudiées dans la partie C.
D.1 Etablir l’équation différentielle du mouvement de M
D.2 Analogie électrique
D.2.1 Ecrire l’équation différentielle des oscillations forcées d’un circuit R L C série.
D.2.2 Définir et exprimer l’impédance complexe mécanique Z’. Que se passe-t-il si w=w0 ?
D.2.3 Calculer l’amplitude vm de la vitesse en fonction de fm, h, q = w/w0 et Q’ (Q’ est défini par analogie avec le coefficient de qualité Q en électricité)
D.2.4 Calculer le déphasage j’ entre la vitesse et la force ![]() .
.
D.3 Calculer en régime forcé, pour w=w0 :
a) L’énergie DW’ dissipée en une période
b) L’énergie cinétique maximale W’c.
c) La différence W’p des énergies potentielles entre x= xm (valeur maximale de x) et x = 0 (équilibre).
d) L’expression b’= 2 p W’c/DW’ : conclure
E Principe d’un sismographe
L’oscillateur mécanique est placé dans un boîtier qui peut effectuer des mouvements de translation verticale. Cet ensemble schématise un sismographe.
La position du boîtier est repérée par la cote A S’= y(t) sur un axe Ay fixe,
Les mouvements imposés au boîtier entraînent des mouvements de M qui sont
repérés par leur abscisse x sur l’axe Ox lié au boîtier.

E.1 Le boîtier effectue des oscillations sinusoïdales forcées y= ym cos wt. En faisant intervenir les grandeurs w0 et Q’=mw0/h, établir l’équation différentielle du mouvement de M par rapport au boîtier en prenant pour variable l’abscisse x(t).
E.2 En régime forcé, x(t) =xm cos(wt + Y) . On pose q = w/w0 et a’= xm/ym
E.2.1 Exprimer a’ en fonction de q et Q’ sous la forme ;
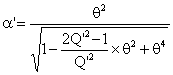
E.2.2 Exprimer tany en fonction de q et Q’
E.3 Les conditions d’utilisation du sismographe sont telles que xm doit être à ym à 2% près, avec Q’ = 1. Déterminer dans quel domaine d’utilisation ces conditions sont satisfaites.
*****
SOLUTION
C.1 On désigne par a l’allongement du ressort à l’équilibre. Dans ce cas, le bilan des forces appliquées sur l’axe vertical Ox descendant s’écrit simplement :
![]()
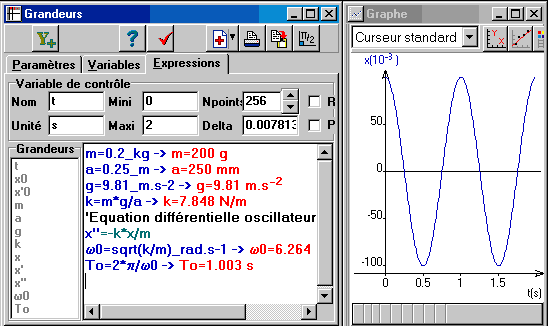
AN Régressi : par exemple si :
m=0.2_kg -> m=200 g
lo=0.1_m -> lo=100 mm
a=0.25_m -> a=250 mm
g=9.81_m.s-2 -> g=9.81 m.sª²
k=m*g/a -> k=7.848 N/m
C.2 Le corps M est assimilable à un point matériel de masse m. La masse du ressort est négligeable. Le référentiel du laboratoire est considéré comme galiléen. Le force exercées sont verticales. L’application de la relation fondamentale de la dynamique conduit à :
![]() ou
ou ![]()
C3 Si l’amortisseur est supprimé, l’équation différentielle est celle d’un oscillateur harmonique :
![]()
![]()
![]()
Résolution avec Régressi
C.4 Reprenons l’équation
différentielle : ![]() et cherchons des
solutions de la forme :
et cherchons des
solutions de la forme : ![]() et écrivons l’équation caractérisquique :
et écrivons l’équation caractérisquique :
![]()
a)
Suivant le signe de D
nous aurons trois régimes possibles :
-- Régime pseudo périodique si D<0

![]()
![]()
La solution générale de l’équation différentielle sera :
![]()
Cette solution est aussi présentée sous la forme :
![]()
![]()
![]()
![]()
![]()
--
Si D=0 le régime est critique :
L’équation caractéristique a une racine double ![]()
![]() est
une première intégrale particulière et on montre aisément que
est
une première intégrale particulière et on montre aisément que ![]() est
une deuxième intégrale particulière linéairement indépendante de la première.
est
une deuxième intégrale particulière linéairement indépendante de la première.
La
solution est donc de la forme :![]()
![]()
![]()
![]()
![]() régime
critique
régime
critique
Si D
> 0 le régime est amorti
Les racines sont réelles 
![]() et
proposons une solution de la forme :
et
proposons une solution de la forme :
![]()
![]()
![]()
![]()
![]()
![]() régime amorti
régime amorti
b) Le régime critique a été obtenu
pour : ![]()
L’application
numérique avec Régressi conduit à
hc=2*sqrt(m*k) -> hc=2.506 kg.s-1
C.5 Exprimons l’énergie cinétique Ec, l’énergie potentielle élastique Ep emmagasinée dans le ressort et l’énergie mécanique Em.
On remarquera l’absence de
l’énergie potentielle de pesanteur. La force ![]() toujours compensée par
la force de rappel du ressort à l’équilibre
toujours compensée par
la force de rappel du ressort à l’équilibre ![]()
Le travail résultant est donc nul :
![]()
Avec Régressi on trace aisément les courbes correspondantes et on montre facilement que l’énergie dissipée dans l’amortisseur durant le régime transitoire est :
![]() énergie initiale
fournie par l’opérateur et emmagasinée dans le ressort sous forme d’énergie
potentielle élastique jusqu’à t=0.
énergie initiale
fournie par l’opérateur et emmagasinée dans le ressort sous forme d’énergie
potentielle élastique jusqu’à t=0.
D Oscillations forcées de l’oscillateur mécanique.
D.1 La force qui s’exerce sur la masse m est : ![]()
Soit sur l’axe
vertical : ![]()
D.2 Définition de l’impédance mécanique
D.2.1 L’équation différentielle d’un circuit RLC s’écrit :
![]()
![]()
Dans le cas de l’oscillateur mécanique comme pour le circuit RLC le régime forcé, solution particulière de l’équation différentielle du second ordre seule quand le régime transitoire solution générale de l’équation différentielle avec second membre nul est amortie
Dans les équations différentielles ci dessus les coefficients ci dessous jouent des rôles analogues.
R Résistance ç=========è h coefficient de frottement
L auto-inductance ç=========è m masse
C capacité ç=========è 1/k inverse de la raideur du ressort
D.2.2 En
électricité l’impédance complexe est ![]()
Pour le
circuit RLC : ![]()
En
mécanique :![]()
![]() Zméca=
h réelle comme Z = R à la résonance dans le circuit RLC.
Zméca=
h réelle comme Z = R à la résonance dans le circuit RLC.
D.2.3 Pour exprimer l’amplitude de la vitesse utilisons la définition de l’impédance mécanique :
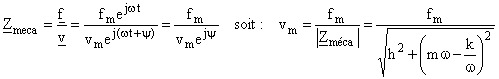
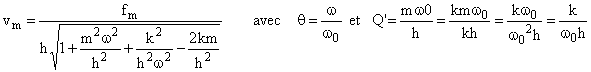

D2.4 Calculons maintenant la phase y
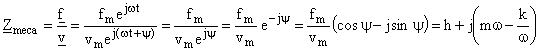
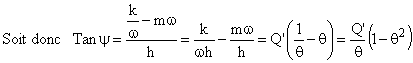
D.3 En régime forcé, pour w = w0 soit pour Zméca= h, calculons :
a) L’énergie dissipée en une période ou encore le travail de la force de frottement :

b)
L’énergie cinétique maximale est ![]()
c) La différence des énergies potentielles entre xm et x = 0
![]()
d) 
On retrouve sous forme énergétique, l’expression de Q’qui caractérise l’acuité de la résonance en mécanique.
E Principe d’un sismographe
E.1 Le référentiel Ox lié à la boite contenant l’oscillateur n’est plus galiléen. Par contre le référentiel Ay peut être considéré comme tel. On peu donc y écrire :
![]() où
où ![]() est
l’accélération absolue,
est
l’accélération absolue, ![]() l’accélération relative,
l’accélération relative,
![]() l’accélération
d’entraînement et
l’accélération
d’entraînement et ![]() l’accélération de
Coriolis. Le mouvement est vertical
l’accélération de
Coriolis. Le mouvement est vertical ![]() .
.
![]()
Le mouvement du boîtier est tel que : ![]()
![]()
E.2 Ici encore après amortissement du régime transitoire, seul subsiste le régime forcé.
Posons : ![]()
E.2.1 Exprimons ![]() en fonction de
en fonction de ![]() et
de Q’
et
de Q’
Reportons la solution proposée dans l’équation différentielle
![]()
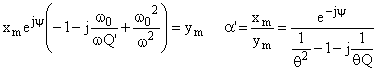

E.2.2 On obtient aussi tan y
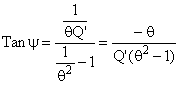
E.3 Si Q’=1 on obtient
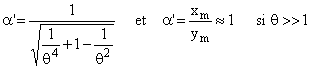

La condition posée correspond donc à ![]()
xm sera egal ym à 2% prés si w = 5 w0