Les modes de fonctionnement possible pour un laser sont au nombre de trois :
Dans ce mémoire nous n'étudions que les deux premiers modes de fonctionnement. Les équations mises en jeu dans ces deux modes de fonctionnement ne sont pas les mêmes et les temps de calcul sont très différents.
En effet la résolution numérique des équations en régime continu avec des faisceaux dont la répartition spatiale est gaussienne est de quelques minutes par point. Alors que la résolution numérique des équations en régime dynamique peut prendre plusieurs dizaines d'heures par point de fonctionnement.
Nous avons donc développé deux modèles numériques :
Ce sont ces deux modèles distincts que nous présentons dans ce
chapitre. Les résultats de ce chapitre n'ont pour but que de donner des ordres de
grandeur des rendements possibles en régime dynamique et d'évaluer les constantes de
temps de " migration " de l'énergie de pompe vers l'énergie laser.
A partir des données obtenues expérimentalement et présentées au chapitre 1, nous avons considéré les paramètres liés au matériau utilisé :
=8,8 ms Ner=1025 m-3
indice du matériau n=1,5 k=10-21 m3s-1
c0=3.108 ms-1 =7.10-25
m2
=1ms
=1,2.10-24 m2
Nyb=1,6 1027 m-3.
Les paramètres de la cavité sont :
longueur de matériau la=2 mm
wp=wl=100 µm ce qui correspond à une surface de 1,57.10-9m2
R=99 %
P=0 % (pas d'autres pertes dans la cavité que celles liées au miroir
de sortie).
En régime stationnaire, nous pouvons écrire : .
A partir de l'équation 3-22 et de l'expression
, on obtient :
|
équation 4-1 |
En prenant un cas simplifié on peut faire tendre vers l'infini la
durée de vie des niveaux 2F5/2 de l'ytterbium et 4I13/2
de l'erbium : et
. Dans ce cas les
équations se simplifient et deviennent :
.
On a donc une puissance de seuil qui tend vers 0 et un rendement qui doit tendre vers le rendement quantique
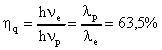
On trouve . Si les seules pertes de la cavité
sont dues à la transmission du miroir de sortie
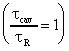
, on a
.
Pour une solution plus complète, on utilise les équations 3-9, 3-10 et
3-16 pour résoudre l'équation 4-1 (voir figure 4-1).
A partir de l'équation 3-9, l'équation 3-11, l'équation 3-12,
l'équation 3-17, l'équation 3-19 et l'équation 3-21, on peut résoudre l'équation 4-1.
Les résultats sont portés sur la figure 4-1.
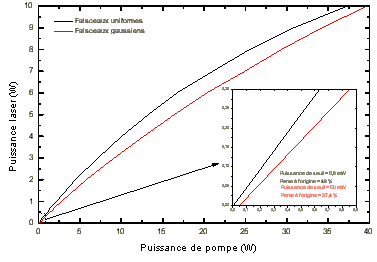
On peut voir sur cette figure que pour une puissance de pompe inférieure à environ 2 W, le phénomène reste linéaire. Au delà de cette puissance de pompe le rendement diminue au fur et à mesure de l'augmentation de la puissance de pompe car progressivement le gain du laser se sature. On peut aussi remarquer que les pentes sont assez élevées (>30 %) aussi bien avec des faisceaux à répartition spatiale uniforme que gaussienne.
On pose N2=n2.Ner, N'3=n'3.Nyb et t=t'.Tar.
L'équation -13-1 devient :
| équation 4-2 |
et l'équation 3-3 s'écrit :
|
équation 4-3 |
Avec des faisceaux uniformes, l'équation 3-22 prend la forme :
| équation 4-4 |
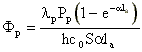
et
.
On résout l'équation 4-2, l'équation 4-3 et l'équation 4-4 par la méthode de
Runge-Kutta :
.
Il est important de connaître l'évolution temporelle du niveau haut (n'3) de l'ytterbium. Pour avoir une solution analytique de l'équation 4-2, on considère que la matrice ne contient pas d'ions erbium, c'est à dire Ner=0. Cette équation devient donc :
dont la solution analytique est :
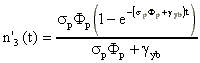
La valeur asymptotique de cette équation est : et
la constante du temps de montée est :
avec =1ms, p=1,375.10-24 m2
et
=7.1025 m2.s-1 ce qui
correspond à une puissance de 1 Watt sur une surface équivalente à celle d'une
gaussienne ayant un rayon au point de focalisation de 100 µm on obtient une valeur
asymptotique de 0,088 et un temps de montée à 90% de la valeur asymptotique de 2 ms
(voir figure 4-2).
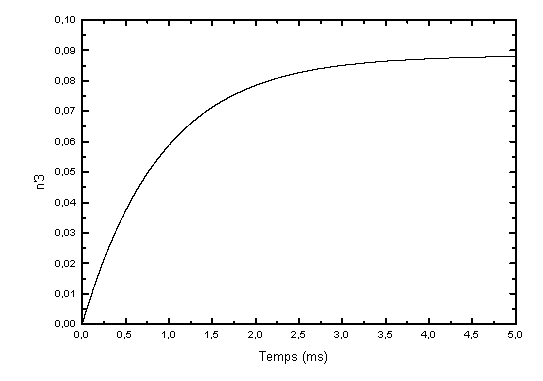
figure 4-2 : Evolution
temporelle de la population du niveau supérieur (2F5/2) de
l'ytterbium.
Il est aussi important d'avoir une idée de la vitesse de
" remplissage " du niveau métastable de l'ion erbium. Pour ce faire
on considère que l'ion ytterbium est un " réservoir " à énergie
constante et que le phénomène laser n'existe pas (pas d'émission induite), de cette
façon l'équation 4-3 devient :
qui a pour solution analytique :
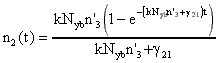
dont la valeur asymptotique est :
et la constante de temps de montée est : .
Avec =8 ms, Nyb=1,6.1027 m-3
et k=10-21 m3s-1 on obtient les résultats reportés sur
la figure 4-3 :
figure 4-3 : Evolution temporelle de la population du niveau métastable (4I13/2) de l'erbium pour différentes populations du niveau supérieur (2F5/2) de l'ytterbium.
Le temps de " remplissage " du niveau métastable
(voir tableau 4-1) de l'ion erbium peut être très différent ( de 4 à 147 µs) selon le
taux de remplissage du niveau haut de l'ytterbium. Il en résulte une dynamique très
différente selon le taux de pompage.
n'3 |
0,3 |
0,1 |
0,05 |
0,01 |
Valeur asymptotique |
1 |
1 |
1 |
1 |
Temps de montée à 90 % (µs) |
4 |
13,6 |
29 |
147 |
Les résultats correspondant à la résolution numérique des équations couplées sont présentés sur la figure 4-4. Dans cet exemple on considère que le matériau est excité pendant 8 ms (environ la durée de vie de l'état métastable de l'ion erbium) la cavité étant bloquée puis on ouvre la cavité ( en un temps infiniment court) qui reste ensuite dans cet état et on arrête l'excitation du matériau.
La figure 4-4 présente une analyse du fonctionnement sur des échelles de temps différentes.
figure 4-4 : Mise en évidence des différents régimes dynamiques du laser.
On observe quatre régimes distincts :
Pendant la dernière phase (figure 4-4d), la population n2 reste constante, on a donc :
dont la solution analytique est :
|
équation 4-5 |
Il est alors possible d'évaluer le coefficient de transfert d'énergie k par l'étude
du comportement dynamique du laser.
Dans cette partie nous nous plaçons dans un fonctionnement où le temps de commutation des pertes n'est plus infiniment court. De plus nous allons simuler le fonctionnement du laser en cadence :
La fréquence de répétition en commutation des pertes est limitée en haute fréquence car le temps d'excitation du matériau est inversement proportionnel à la fréquence de répétition. Il est difficile d'établir une fréquence limite de manière analytique. Car si à l'instant de la première ouverture de cavité la population du niveau métastable n'est pas supérieure à la population seuil, cette condition pourra être vérifiée à la énième ouverture de cavité. Les calculs présentés dans ce paragraphe sont effectués avec une puissance de pompe de 1 W.
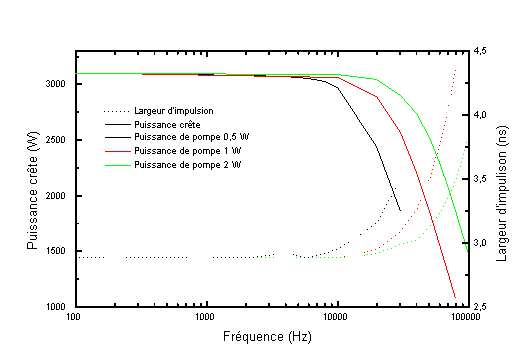
La puissance crête et la largeur d'impulsion ont donc été calculées pour plusieurs fréquences de répétition et pour plusieurs puissances de pompe. Les résultats sont reportés sur la figure 4-5. On peut donc voir qu'avec ces conditions de calcul, on obtient une chute d'un facteur deux sur la puissance crête pour une fréquence de répétition qui varie avec la puissance de pompe. En effet, l'ion ytterbium se comporte, vis à vis de l'ion erbium, comme un " réservoir " à énergie. Le dépeuplement du niveau haut de la transistion laser due à l'impulsion de commutation des pertes est compensé très rapidement par le transfert énergétique de l'ion ytterbium vers l'ion erbium. Il suffit simplement qu'entre deux impulsions le niveau haut de l'ytterbium ait eu le temps de se repeupler de la quantité transférée à l'ion erbium. Ce temps est d'autant plus court que la puissance de pompe est élevée.
Pour des systèmes de commutation des pertes relativement lents (supérieurs à 60 ns), la puissance crête restituée sera inférieure à celle calculée. Il faut donc prendre en compte le temps de commutation du système. Le temps de commutation est défini figure 4-6.
Avant t=0, les pertes sont de 100 %.
A t=0, les pertes diminuent linéairement.
Après le temps de commutation, les pertes sont égales aux pertes
intrinsèques de la cavité.

figure 4-6 : Définition du
temps de commutation des pertes.
Si le temps de commutation est trop important, l'énergie restituée dans l'impulsion n'est pas maximale. On a donc une diminution de la puissance crête et une augmentation de la largeur d'impulsion (voir figure 4-7). Pour un temps de commutation supérieur à 65 ns, on a une diminution d'un facteur deux de la puissance crête.
Nous avons donc obtenu un ordre de grandeur des puissances de pompe au seuil et des rendements possibles en régime continu. En régime dynamique, les ordres de grandeur des temps de " migration " de l'énergie de l'ion ytterbium vers l'ion erbium ont été calculés. Nous avons trouvé une méthode pour estimer le coefficient de transfert d'énergie. Les ordres de grandeur des temps de commutation et fréquence de répétition maxima pour avoir une énergie restituée maximale ont été estimés.
Dans le chapitre suivant, nous présentons tous nos résultats
expérimentaux effectués sur ce laser.
Chapitre suivant