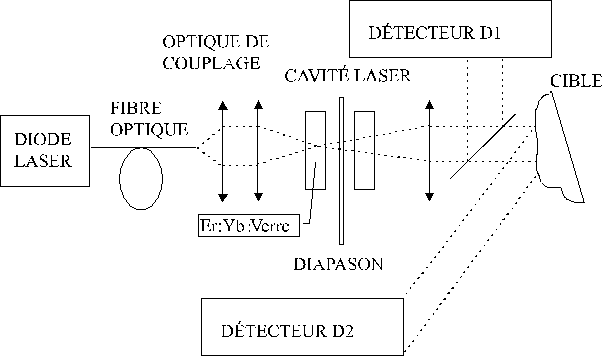
Un laser impulsionnel à sécurité oculaire (émettant dans la fenêtre spectrale proche de 1,5 µm) compact et peu onéreux peut être utilisé en télémétrie. Il existe de nombreuses solutions envisageables pour produire une émission laser à cette longueur d'onde qui sont représentées par :
L'emploi d'un laser verre codopé erbium et ytterbium pompé par une diode laser de puissance semble être une solution adaptée pour certaines applications relevant de la télémétrie courte portée. Il faut néanmoins que le système de commutation des pertes soit rustique afin de satisfaire le critère de bas coût.
Les systèmes mécaniques simples ne présentent pas les mêmes
rendements potentiels que les systèmes habituellement utilisés (acousto-optique,
électro-optique, ...).Mais ces derniers sont inadaptés à la configuration que nous
avons adoptée. En effet la géométrie utilisée est une cavité à miroirs plans
parallèles de quelques millimètres de long. Cette cavité est stabilisée par le guidage
par le gain et les éventuelles lentilles thermiques se créant dans le matériau. Avec
une longueur de cavité supérieure à 2 ou 3 cm (encombrement d'un système de
déclenchement standard), le laser ne fonctionne plus ou devient très multimode
transverse. De plus le gain maximal possible dans le matériau étant d'environ 3% pour un
aller et retour dans la cavité, il faudrait que les pertes dues à l'insertion d'un
déclencheur dans la cavité soient inférieures à 1% sur un aller et retour dans la
cavité laser.
La sortie de la fibre optique est imagée avec un grandissement d'environ 2 dans le matériau actif. Le verre : Er : Yb a une épaisseur de 2 mm dont une face est traitée Rmax à 1,54µm et Tmax à 980nm et l'autre face antireflet à 1,54µm. Le miroir de sortie a une réflexion de 99% à 1,54µm. La distance entre la pastille de verre et le miroir de sortie permettant l'insertion du diapason dans la cavité est de 2 ou 3 mm (voir figure 9-1).
En sortie de cavité laser, le faisceau est collimaté par une lentille
de 50 mm de focale.
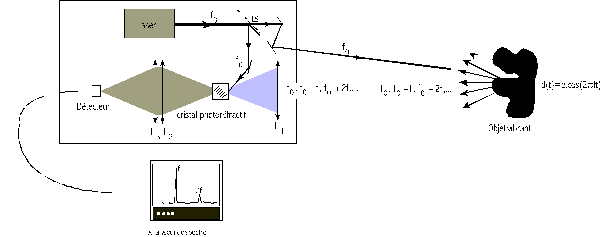
figure 9-1 : Schéma de
principe du télémètre.
figure 9-2 : Photo de la maquette de télémétrie
figure 9-3 : Photo de la cavité laser.
Le système du télémètre est fondé sur la mesure du temps de vol
d'une impulsion. Le détecteur D1 recueille l'impulsion initiale qui, dès qu'elle
dépasse une certaine tension, déclenche un compteur. Le flux rétrodiffusé par la cible
est collecté par une lentille de Fresnel de diamètre 6cm qui le focalise sur le
détecteur D2. L'apparition de l'impulsion de retour arrête le compteur. Connaissant le
temps d'aller et retour de l'impulsion entre l'appareil et la cible et la vitesse de la
lumière dans l'air, on peut ainsi connaître la distance les séparant.
Pour une puissance de pompe continue d'environ 700 mW, on obtient une
émission laser à 1,535 µm monomode transverse à une cadence de 800 Hz. Au lieu
d'engendrer une impulsion unique en exploitant le mécanisme de déclenchement par
commutation des pertes, le laser génère en fait un train de quatre impulsions (voir
figure 5-33). La première impulsion présente une largeur à mi-hauteur de 60 ns et une
puissance crête de 50 W.
Le fonctionnement du télémètre n'est pas perturbé lorsqu'il y a un
train de plusieurs impulsions.
Pour une puissance de pompe continue d'environ 700 mW, on obtient une émission laser à 1,535 µm monomode transverse à une cadence d'environ 400 Hz. Au lieu d'engendrer une impulsion unique en exploitant le mécanisme de déclenchement par commutation des pertes, le laser génère en fait un train de deux impulsions (voir figure 5-32). La première impulsion présente une largeur à mi-hauteur de 35 ns et une puissance crête de 120 W.
Un oscillogramme des impulsions d'émission et de réception est
présentée sur la figure 9-4. La distance séparant le télémètre de la cible est de 32
m. On mesure un temps de vol aller et retour de l'impulsion laser de 200 ns. La distance
mesurée est donc de : où c0 est la vitesse de la
lumière et t est le temps séparant l'impulsion émise de l'impulsion reçue. La distance
affichée par le télémètre est de 33 m. La valeur affichée est bien dans l'intervalle
valeur réelle plus ou moins la résolution (3 m).
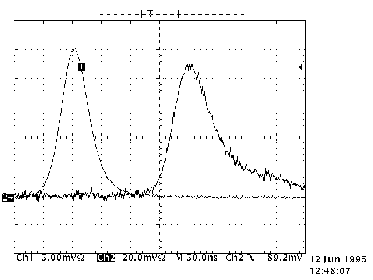
figure 9-4 : Impulsion émise et reçue par la maquette de télémétrie.
La portée du télémètre est donnée par le signal de retour minimal détectable, qui est imposé par le bruit de la chaîne de détection :
| équation 9-1 |
RS/B : rapport signal à bruit,
S : sensibilité de la chaîne de détection (V/W),
PS : puissance reçue (W),
PD : puissance de bruit en l'absence de signal optique dans une bande de 1Hz (W/Hz),
B : bande passante de la chaîne de détection (Hz),
J : composante du bruit de grenaille.
Le bruit de grenaille est négligeable (non mesurable) pour le système de détection
utilisé.
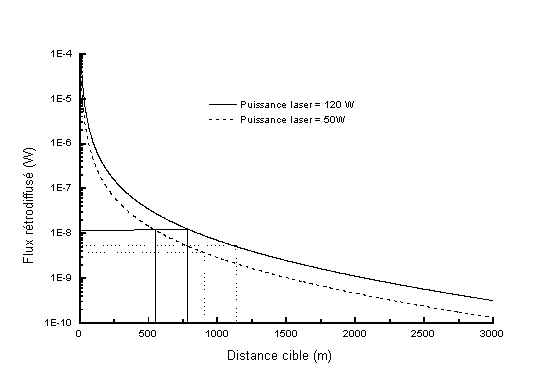
En prenant un rapport signal à bruit de 50 (RS/B=50), PD=1,2.10-18 W/Hz, B=100 Mhz et S=6540 V/W, on trouve un signal minimal détectable de 12 nW. La portée est alors donnée par la loi de Bouguer [39] qui permet de calculer la puissance rétrodiffusée par une cible lambertienne d'albédo :
| équation 9-2 |
: caractérise le pouvoir rétrodiffusant d'une cible,
: diamètre de la pupille de réception,
d : distance cible,
Plaser : puissance laser,
Tatm : transmission de l'atmosphère à la longueur d'onde utilisée.
En prenant un albédo de 0,1 pour la cible, on obtient une portée de 700 m.
On peut augmenter cette portée en diminuant la bande passante de la chaîne de détection de façon à optimiser le rapport signal à bruit tout en conservant une bonne réponse.
Cette optimisation se réalise à l'aide d'un filtre électronique
" passe bas " du deuxième ordre. La réponse temporelle de ce type de
filtre de fréquence de coupure fc à -3 dB est divisée en deux catégories :
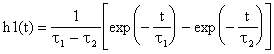
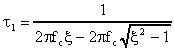
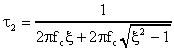
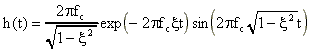
Le signal électrique s(t) de sortie d'un filtre électronique de
réponse impulsionnelle h(t) et de signal d'entrée e(t) est : 
Dans notre cas le signal d'entrée est une gaussienne temporelle de
durée à mi-hauteur : 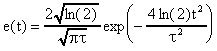
Dans un premier temps, il convient de déterminer le type de filtre se prêtant le mieux à l'optimisation souhaitée sans pour autant déformer trop fortement l'impulsion d'entrée. Il faut donc déterminer le coefficient pour lequel le filtre correspondant déforme le moins l'impulsion d'entée.
La figure 9-5 présente les réponses temporelles des différents
filtres dont la fréquence de coupure est où est la largeur à
mi-hauteur de l'impulsion gaussienne d'entrée.
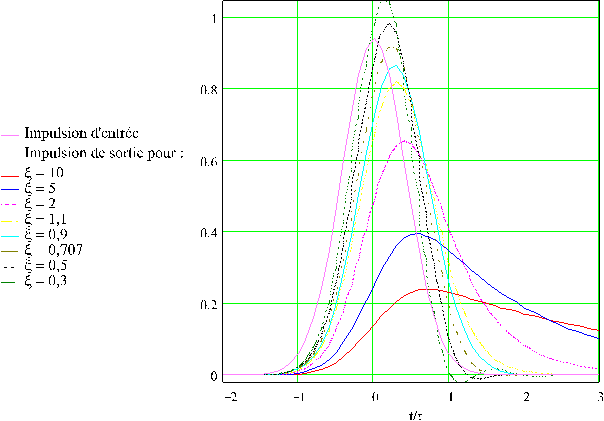
Le filtre pour lequel l'impulsion d'entrée semble la moins déformée
est un filtre sous-amorti de coefficient d'amortissement .
Le dernier paramètre ajustable est la fréquence de coupure à -3 dB du filtre.
Le rapport signal à bruit est proportionnel à
(voir figure 9-6) où est l'atténuation en tension dû au filtre (
).
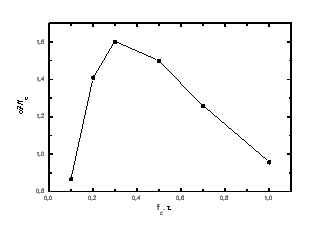
figure 9-6 : Variations de en fonction de
.
Cette fonction passe par un maximum pour . Pour
des commodités de calcul au lieu de faire apparaître dans le rapport signal à bruit on
définit une bande passante équivalente de bruit
.
La figure 9-7 représente les impulsions à l'entrée et à la sortie du
filtre choisi.
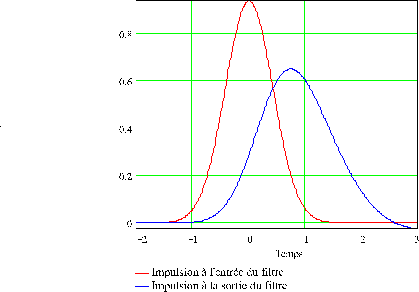
Le filtre optimal est donc un filtre sous-amorti du deuxième ordre de
coefficient d'amortissement et de fréquence de coupure
où est la largeur à mi-hauteur de l'impulsion gaussienne.
On trouve donc :
L'albédo d'un véhicule automobile est difficilement définissable, car certaines parties pourront avoir un albédo équivalent de :
Nous avons donc pris une valeur moyenne relativement défavorable de 0,1 qui correspond à peu près à l'albédo d'un mur sombre.
La résolution est limitée par la fréquence d'horloge du compteur, car
l'écart de temps minimum mesurable correspondant à la distance minimale d'aller et
retour est une période d'horloge. Si f=60Mhz, la résolution est
où c0 est la vitesse de la lumière dans l'air.
Nous avons donc réalisé et testé en fonctionnement un laser à
sécurité oculaire déclenché par un système mécanique rustique et dont les
performances en termes de puissance crête et de largeur d'impulsion nous ont permis
d'élaborer la maquette d'un télémètre dont les performances sont compatibles avec les
applications relevant de la localisation de mobiles ou d'obstacles.
Cette application entre dans le cadre d'un travail de thèse effectué
au Laboratoire Central de Recherches de Thomson en collaboration avec Thomson CSF
Optronique [40]. Dans
ce cadre une maquette d'analyse de vibrations a été réalisée. Cette maquette repose
sur le mélange à deux ondes dans un cristal photoréfractif (CdTe). La longueur d'onde
du faisceau laser utilisé est 1,54 µm. Ce faisceau doit présenter une répartition
spatiale parfaitement gaussienne et être monofréquence.
Le principe de la détection hétérodyne grand champ associée à l'analyse de vibrations est décrit par la figure 9-9. Un laser monofréquence de fréquence f0 émet un faisceau qui est divisé en deux par une lame séparatrice LS. Le faisceau transmis illumine l'objet qui vibre à une fréquence f. La lumière diffusée ou réfléchie par l'objet possède un spectre discret en fréquence aux fréquences f0, f0+f, f0-f, etc...Elle est collectée par la lentille L1 qui focalise le faisceau (appelé faisceau signal) dans le cristal photoréfractif. Le faisceau réfléchi par la lame séparatrice LS est le faisceau pompe. Les interférences de celui-ci avec la composante du faisceau signal à la fréquence f0 créent un réseau d'indice dans le cristal. Le faisceau pompe se diffracte sur ce réseau, générant ainsi un oscillateur local adapté au signal (même front d'onde et même direction) de fréquence f0. La lentille L2 collecte les faisceaux signal et oscillateur local qui sont focalisés par la lentille L3 sur la surface du détecteur. Celui-ci délivre un photocourant aux fréquences f, 2f, etc... Le détecteur est connecté à un analyseur de spectre qui donne l'amplitude de la composante à la fréquence f (2f, etc...). Celui-ci dépend de l'amplitude de la vibration de l'objet. On mesure ainsi la fréquence et l'amplitude de la vibration de l'objet.
Notre laser étant parfaitement gaussien et présentant peu de modes
longitudinaux, il semblait possible d'obtenir un effet similaire à celui obtenu avec un
laser monofréquence. En effet, le principe repose sur l'inscription dynamique d'un
réseau d'indice dans le matériau. Si le laser est multimode longitudinalement, nous
obtiendrons un réseau d'indice par mode longitudinal. Si le laser est fortement multimode
longitudinal, il y aura un grand nombre de réseaux inscrits dans le matériau et la
figure d'interférence sera complètement " illisible ". Par contre si
le laser est faiblement multimode longitudinal (2 ou 3 modes), il y aura 2 ou 3 réseaux
d'indice inscrits dans le matériau et la figure d'interférence correspondante sera
utilisable. Nous avons donc remplacé le laser monomode par notre laser présentant 3
modes longitudinaux. Nous avons pu détecter des vibrations et obtenir un effet du même
ordre qu'avec le laser monomode. Néanmoins ces expériences ne sont pas terminées car il
reste à caractériser la détectivité du système avec les deux types de laser à
puissance égale.
Chapitre suivant