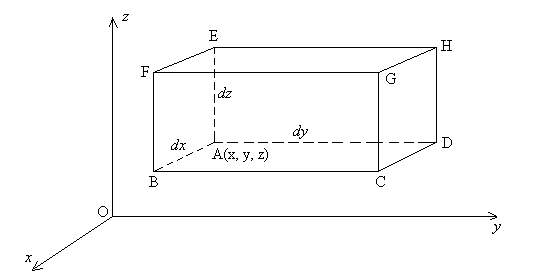Statique des fluides
Plan
1. Pression dans un fluide au repos (en
équilibre dans un référentiel galiléen)
1.1. Etude expérimentale dans le champ de pesanteur
1.2. Définition de la pression dans un fluide
1.3. Relation locale traduisant l’équilibre d’un
fluide dans un référentiel galiléen
2. Cas d’un fluide au repos dans le champ de pesanteur
2.1. Surface de séparation entre deux fluides non
miscibles au repos
2.2. Fluide incompressible (liquide)
2.3. Fluide compressible (gaz)
2.4. Théorème d’Archimède et corps
flottants
3. Relation locale traduisant l’équilibre d’un fluide
dans un référentiel non galiléen
4. Phénomènes de tension superficielle
4.1. Tension superficielle
4.2. Loi de Laplace
4.3. Capillarité. Loi de Jurin
4.4. Mesure des tensions superficielles
Exercices - types
1. Pression dans un fluide au repos (en équilibre
dans un référentiel galiléen)
Notre sens commun nous fait appréhender un fluide (gaz ou liquide) comme étant de nature très différente d’un solide. Ce dernier a une forme propre qui nous permet de le reconnaître. Liquide ou gaz n’ont pas de forme propre, ils épousent la forme du récipient qui les contient, sont déformables sous la moindre action. Liquide et gaz ont des différences : un liquide, contrairement à un gaz, a un volume défini, il ne remplit pas tout le volume du récipient.
1.1. Etude expérimentale dans le champ
de pesanteur
|
|
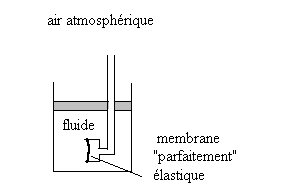
- Le tube en U avec la membrane élastique est placé dans l’air atmosphérique : la membrane n’est pas tendue.
- Nous plaçons l’extrémité avec membrane dans un
liquide (ou dans un gaz dont on peut faire varier le volume à
l’aide d’un piston) : la membrane élastique est tendue comme
indiqué sur la figure ; ceci traduit des efforts du fluide
sur la membrane
|
La forme de la membrane est indépendante de l’orientation
de la membrane autour d’un même point, les efforts sur la membrane sont
perpendiculaires à celle-ci.
Si le fluide est un liquide, la déformation de la membrane augmente de
manière significative avec la profondeur.
Autre expérience : si, dans un récipient contenant un liquide, nous perçons un trou, l’écoulement de liquide se produit perpendiculairement à l’orifice quelque soit l’orientation de ce dernier.
1.2. Définition de la pression dans
un fluide
|
|
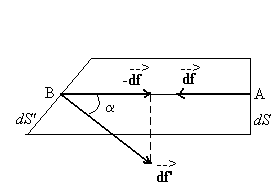
Considérons un fluide en équilibre dans un référentiel lié au sol supposé galiléen et une portion de ce fluide limitée extérieurement par un cylindre élémentaire de révolution d’axe AB horizontal et dont les bases sont, en A une section droite dS, en B la surface plane dS’ dont la normale fait un angle a avec l’axe AB.
Nous avons 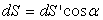 . .
|
Cette portion de fluide n’est pas soumise qu’à son seul
poids (voire à d’autres forces dues à un champ extérieur)
pour être en équilibre. Elle est soumise à des forces " superficielles "
(sur les surfaces délimitant le cylindre) dues au fluide extérieure
environnant la portion, les forces internes à la portion n’interviennent
pas car elles obéissent au principe de l’action et de la réaction.
Les forces 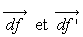 exercées
par le fluide environnant sur les bases (non matérielles) dS et dS’ du
volume élémentaire de fluide sont normales à celles-ci
(sinon il y aurait glissement entre les couches du fluide puisqu’un fluide se
déforme à la moindre action extérieure).
exercées
par le fluide environnant sur les bases (non matérielles) dS et dS’ du
volume élémentaire de fluide sont normales à celles-ci
(sinon il y aurait glissement entre les couches du fluide puisqu’un fluide se
déforme à la moindre action extérieure).
La condition d’équilibre sur l’axe horizontal se traduit par 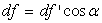 .
.
Soit 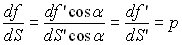 qui, par
définition, est la pression dans le fluide.
qui, par
définition, est la pression dans le fluide.
La pression p en un point d’un fluide en équilibre est indépendante de l’orientation de l’élément de surface qui sert à la définir.
La pression est une grandeur scalaire positive, la force de pression est une grandeur vectorielle.
La pression est la même en tous les points d’un plan horizontal pris dans un fluide en équilibre.
1.3. Relation locale traduisant l’équilibre
d’un fluide dans un référentiel galiléen
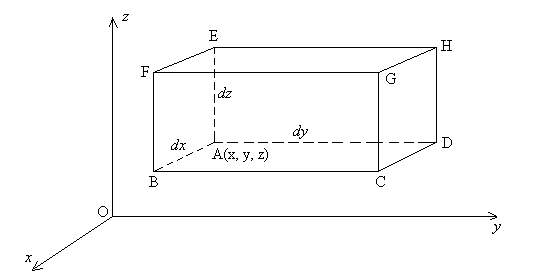
Exprimons la relation d’équilibre pour un élément
de fluide en forme de parallélépipède rectangle de dimensions
dx, dy et dz à partir du point A de coordonnées
x, y et z.
Sur la surface rectangulaire ABFE, nous avons une pression 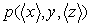 et, sur la surface rectangulaire DCGH, nous avons une pression
et, sur la surface rectangulaire DCGH, nous avons une pression 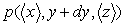 .
.
Il en est de même sur les autres faces du parallélépipède
rectangle en permutant les coordonnées. Les forces dues à des
champs de forces extérieures s’écrivent 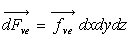 .
.
En appliquant les relations d’équilibre de la Mécanique et en
projetant suivant la direction Oy, on obtient 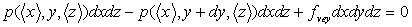 .
.
Soit encore 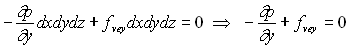 ;
; 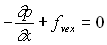 ;
; 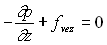
Sous forme vectorielle, ces trois dernières relations
s’écrivent : 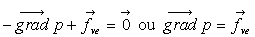

Remarque : le gradient de pression n’est due qu’aux champs de forces extérieures.
2. Cas d’un fluide au repos dans le champ de
pesanteur
Principe de l’hydrostatique
Le fluide a pour masse volumique m
et le champ de pesanteur est le seul champ de forces extérieures.
Dans ce cas 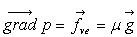 relation équivalente à
relation équivalente à 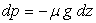 si l’axe
si l’axe 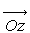 est vertical
ascendant. Ceci constitue le principe de l’hydrostatique.
est vertical
ascendant. Ceci constitue le principe de l’hydrostatique.
Remarque sémantique : nous avons employé le mot "Principe" pour traduire une relation (démontrée à partir du principe fondamental de la Mécanique) ; nous aurions du dire Théorème ; en fait, cela se produit souvent en Physique : ce qui était un Principe à une époque devient un Théorème avec l'avancement des connaissances et, souvent, à tort, on garde la première terminologie.
Autre démonstration :
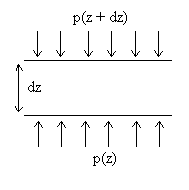
L’augmentation de pression entre une altitude z + dz
et une altitude z est due au poids du fluide dans le cylindre de hauteur
verticale dz et de surface horizontale unitaire.
L’évolution de pression est donc continue, même à la séparation
de deux fluides.
La pression a une altitude z est égale au poids, par unité
de surface horizontale, des couches de fluide situées à la verticale
au-dessus de z.
Dans un même fluide au repos, les surfaces d’égale altitude sont
isobares (même pression).
Dans le système MKSA, les pressions se mesurent en N m-2
que l’on appelle Pascal (Pa).
Attention, il ne faudrait pas conclure que les forces de pression s’exercent verticalement. Elles s’exercent perpendiculairement à tout élément de surface.
2.1. Surface de séparation entre deux
fluides non miscibles au repos
Considérons deux points de cette surface. Soit dz
leur différence d’altitude.
On peut écrire, en négligeant toute discontinuité de la
pression à la traversée de la surface de séparation : 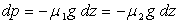 ce qui entraîne dz = 0.
ce qui entraîne dz = 0.
La surface de séparation entre deux fluides non miscibles au repos est plane et horizontale.
L’étude de la stabilité de l’équilibre montrerait que le liquide de densité plus faible se place au dessus de celui de densité plus forte.
2.2. Fluide incompressible (liquide)
La masse volumique est constante et l’intégration du
principe de l’hydrostatique donne 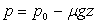 Cette relation est souvent appelée principe de Pascal
Cette relation est souvent appelée principe de Pascal
Applications : baromètre - presse hydraulique
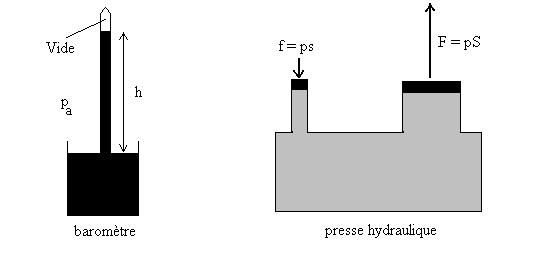
Dans un baromètre à mercure, pour une pression
atmosphérique normale, la hauteur h est égale à 760 mm
ce qui correspond à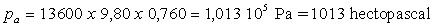
Souvent, les pressions sont exprimées en mm de mercure, en atmosphère
( 1 atm correspond à la pression atmosphérique normale), en bar
(1 bar = 105 Pa) ou millibar (mbar).
Nous remarquerons que pour une hauteur d’eau de 3m, la variation de pression
est égale à 30000 Pa soit à peu près le tiers de
la pression atmosphérique normale.
A l’échelle humaine courante, les variations de pression sont sensibles dans les liquides.
Un baromètre mesure une pression absolue puisque la
pression dans le vide est nulle (pas de masse = pas de poids). Les manomètres
qui mesurent les différences de pression seront étudiés
en Travaux dirigés et pratiques.
2.3. Fluide compressible (gaz)
La masse volumique dépend de la pression et nous le
verrons de la température. On ne peut intégrer directement
la relation dp = -mg dz.
Cependant les masses volumiques des gaz sont faibles (air dans les conditions
courantes 1,3 Kg m-3) et, à
l’échelle humaine courante, on négligera les variations de pression
avec l’altitude dans les gaz.
Seul l’air atmosphérique présente des différences d’altitude
suffisantes pour ne pas négliger les variations de pression (il faut
compter de l'ordre de 1 km d'altitude pour que les variations de pression
deviennent significatives).
2.4. Théorème d’Archimède
et corps flottants
Théorème d’Archimède
Considérons (Fig. a) un corps entièrement immergé dans un fluide homogène au repos. Il occupe un volume V et subit de la part du fluide des forces de pression.
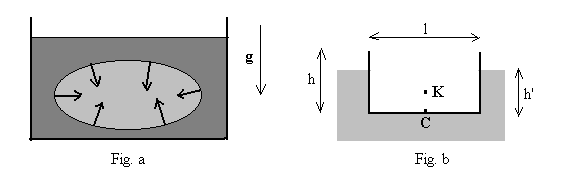
" Tout corps plongé dans un fluide en équilibre est soumis de la part de celui-ci à une poussée verticale, dirigée de bas en haut, égale au poids du fluide de remplacement et appliquée à son centre de masse appelé centre de carène. "
Démonstration : En effet, en l’absence de
corps immergé, le fluide de remplacement serait en équilibre sous
l’action des forces de pression exercées par le fluide environnant et
des forces de pesanteur. La résultante des forces de pression exercées
par le fluide environnant est donc l’opposé du poids du fluide de remplacement.
Autre démonstration : nous appliquons le
théorème du gradient (cas particulier du théorème
d’Ostrogradsky) pour la résultante des forces de pression sur une surface
fermée S contenant le volume V.
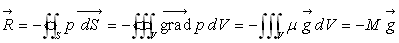 (le vecteur
(le vecteur
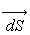 est orienté
vers l’extérieur de la surface fermée).
est orienté
vers l’extérieur de la surface fermée).
On montre aussi que le centre d’application des forces de pression
est confondu avec le centre de poussée des forces de pesanteur aplliquées
sur le fluide de remplacement.
Ce théorème reste vrai si le corps est immergé dans plusieurs
fluides en équilibre.
Statique des corps flottants
Lorsque le poids du liquide de remplacement est supérieur au poids du corps, seule une partie de ce dernier est immergée. Le corps est alors soumis à deux forces : son poids, appliqué au centre de masse C, et la poussée d’Archimède appliquée au centre de carène K.
A titre d’exemple, considérons l’équilibre
d’une boîte parallélépipèdique à section rectangulaire
ouverte flottant sur l’eau (Fig. b). Une telle boîte, de dimensions L
= 10 m, l = 4 m, h = 3 m et de masse M = 20
t, constitue un modèle simplifié d’une embarcation flottant
sur l’eau. Elle s’enfonce dans l’eau d’une hauteur h’ telle que :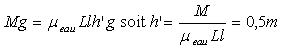
Notons
que, la boîte étant ouverte et les parois latérales de masse
négligeable, le centre de masse C est situé au centre de la base
rectangulaire, alors que le centre de carène K est au- dessus de lui
à la distance h’/2 . Dans ce cas, l’équilibre est stable
: une légère rotation de la boîte autour de l’axe longitudinal
passant par le centre de masse produit des oscillations autour de la position
d’équilibre.
L’étude de la stabilité de la position d’équilibre
n’est pas abordée.
3. Relation locale traduisant l’équilibre
d’un fluide dans un référentiel non galiléen
En Mécanique, on apprend que le mouvement d’une masse
" ponctuelle " m (mieux : le mouvement du
centre de masse d’un système matériel de masse totale m)
est régi, dans un référentiel non galiléen, par
la relation 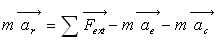 où on introduit les forces d’entraînement et de Coriolis.
où on introduit les forces d’entraînement et de Coriolis.
L’absence de mouvement relatif imposent accélération et vitesse
relatives nulles et donc 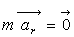 et
et 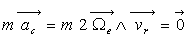
Par suite, la relation d’équilibre s’écrit 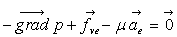 .
.
Pour le champ de forces extérieures de pesanteur 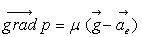
4. Phénomènes de tension superficielle
Une molécule au sein d’un liquide est soumise de la
part des autres molécules à des forces de Van der Waals
d’origine électromagnétique qui varient en 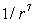 .
Ce type d’interaction décroît très rapidement et peut être
négligé au-delà d’une distance de l’ordre d’une dizaine
de nanomètres.
.
Ce type d’interaction décroît très rapidement et peut être
négligé au-delà d’une distance de l’ordre d’une dizaine
de nanomètres.
A la surface de séparation de deux fluides (liquide-gaz ou liquide-liquide),
la situation est différente en particulier l’isotropie des forces qui
existe au sein d’un fluide n’est plus la règle et il apparaît un
système de forces différent dans la couche capillaire (couche
de liquide proche de la surface de séparation de deux fluides et dont
l’épaisseur est de l’ordre du nanomètre).
A titre d’exemples, chacun visualisera que l’on peut soulever une pellicule
d’eau savonneuse avec un anneau et qu’en soufflant sur cette pellicule on peut
former un bulle de savon dont la surface en forme de sphère est tendue.
4.1. Tension superficielle
|
|
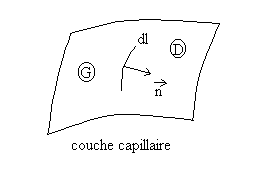
Les phénomènes observés suggère
de traiter la couche capillaire comme une membrane élastique
supposée d’épaisseur nulle.
Effectuons une incision de longueur dl dans la couche capillaire.
Les lèvres s’écartent ce qui signifie que préalablement
à l’incision, la partie droite D de la couche capillaire exerçait
sur l’élément dl appartenant à la partie de
gauche G une force attractive  où A, coefficient de tension superficielle s’exprime
en
où A, coefficient de tension superficielle s’exprime
en 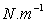 . .
Remarque : La partie droite D de la couche capillaire peut
être remplacée par un solide, la force garde la même
valeur.
|
|
Liquide
|
A (N.m-1) |
t ( °C ) |
|
|
Eau |
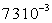
|
20 |
|
|
Ethanol |
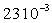
|
20 |
|
|
Glycérine |
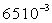
|
20 |
|
|
Eau |
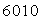
|
60 |
|
4.2. Loi de Laplace
4.3. Capillarité. Loi de Jurin
|
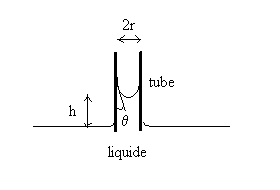
Plongeons un tube de faible diamètre (capillaire)
dans un liquide contenu dans une cuve de grandes dimensions.
Le liquide s’élève dans le tube. Ce phénomène
s’appelle capillarité et la loi de Jurin permet d’en rendre
compte.
A partir de loi de Laplace, on montre la loi de Jurin : 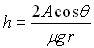
|
|
L’angle q de contact dépend de l’interface : il est de 0° pour les interfaces eau-verre propre et éthanol-verre propre et respectivement de 140°, 90° et 107° pour les interfaces mercure-verre, eau-argent et eau-paraffine.
4.4. Mesure des tensions superficielles
Il existe plusieurs méthodes de mesure des tensions
superficielles. Nous citerons celle utilisant directement la loi de Jurin, celle
utilisant l’arrachement d’un solide du liquide et celle utilisant le détachement
des gouttes de liquide d’un tube.
Exercices - types
|
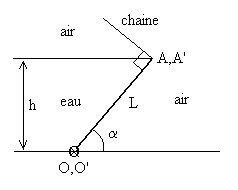
1 – La figure ci-contre représente une
vanne rectan-gulaire (L x l) en coupe verticale destinée
à fixer le niveau d’eau (hauteur h) d’une retenue. Cette
vanne est articulée à sa base sur un axe OO’ et maintenue
au sommet par 2 chaînes parallèles manoeuvrées par
un treuil. En position haute (angle a) on supposera
la direction des chaînes perpendiculaires à la vanne.
1) Calculer la poussée sur la vanne due à
la pression hydrostatique et son centre d’application.
|
|
2) Calculer les efforts transmis aux chaînes (on négligera
le poids propre de la vanne) et la réaction de l’axe OO’.
Application
numérique : h = 4m ; L = 5m ; l
= 6m
2 - On remplit d’eau sur une hauteur h un verre de forme cylindrique. On appelle S la section
de sa base.
1) Calculer la résultante des forces de pression sur
les parois du verre. Interpréter le résultat
2) Mêmes questions avec un verre en forme de cône,
un verre ballon.
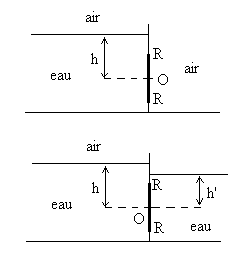
| 3 - Une vanne de vidange est constituée
par un disque de rayon R pivotant autour d’un axe horizontal. Le
centre O du disque est positionné à une hauteur h par
rapport au niveau d’eau.
1) Calculer la poussée sur le disque et la position
du centre de poussée.
2) Reprendre le calcul dans le cas où le disque
est noyé (eau de chaque coté du disque). Ce cas est celui
d’une écluse.
Application numérique : h = 2m
; R = 0,5m
|
|
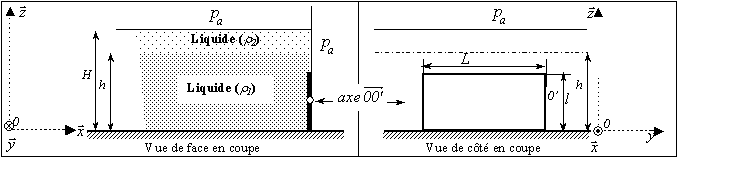
4 - Une vanne plane verticale de forme rectangulaire
(largeur L et de hauteur l), articulée autour d’un axe
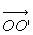 (figure ci-dessous),
maintient le niveau de deux liquides non miscibles de masses volumiques respectives
(figure ci-dessous),
maintient le niveau de deux liquides non miscibles de masses volumiques respectives
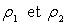 . Le niveau
du liquide de masse volumique
. Le niveau
du liquide de masse volumique 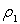 se situe à une hauteur h (le liquide 1 dépasse l’extrémité
haute de la vanne). L’autre liquide de masse volumique
se situe à une hauteur h (le liquide 1 dépasse l’extrémité
haute de la vanne). L’autre liquide de masse volumique 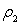 est situé à une hauteur H-h au de dessus du premier liquide.
La face de la vanne du côté liquide est complètement noyée
dans le liquide de masse volumique
est situé à une hauteur H-h au de dessus du premier liquide.
La face de la vanne du côté liquide est complètement noyée
dans le liquide de masse volumique  .
.
1) Calculer la force de poussée due à la pression
hydrostatique du liquide s’exerçant sur la face verticale de la vanne.
2) Déterminer la position du point d’application C
de cette poussée en fonction de 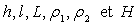 .
.
On vérifiera que 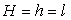 ð
ð 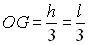
|
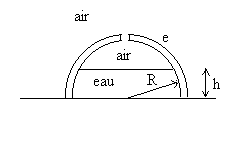
5 - Une cloche hémisphèrique ( rayon
R, épaisseur e<< R, masse m) repose sur un
plan horizontal.
Elle contient de l’eau jusqu’à une hauteur h. Un orifice
pratiqué au sommet permet de maintenir la pression atmosphèrique
à l’interface eau/air.
L’épaisseur de paroi e est suffisamment
faible pour considérer comme identiques les surfaces intérieure
et extérieure de la cloche.
|
 |
Montrer qu’il existe une hauteur critique 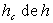 au
delà de laquelle l’équilibre est rompu (la cloche se soulève)
Application numérique : cloche en verre de densité d = 2,5
telle que e/R = 0,02
au
delà de laquelle l’équilibre est rompu (la cloche se soulève)
Application numérique : cloche en verre de densité d = 2,5
telle que e/R = 0,02
|
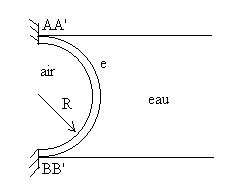
6 - Etude succincte d’un barrage voûte en
forme de
½ cylindre (épaisseur de paroi e, rayon moyen R,
hauteur h ; e/R << 1).
Ce barrage est en appui selon AA’ et BB’ (parallèle à l’axe
z vertical de la voûte).
Calculer la poussée totale sur le barrage et la réaction
des appuis.
Application numérique : h = R =
100m ; e = 10m
|
|
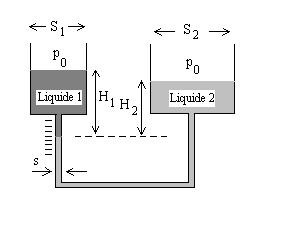
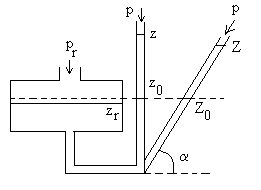
7 - La figure schématise un manomètre
à liquide (masse volumique m) à
réservoir de section
|
|
constante S ; celle du tube vertical est s.
Lorsque 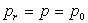 ,
on a ,
on a 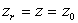 repérable
à travers le tube. Lorsque repérable
à travers le tube. Lorsque 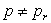 ,
les cotes des deux surfaces libres deviennent ,
les cotes des deux surfaces libres deviennent 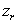 et z, cette dernière cote étant seule repérable.
et z, cette dernière cote étant seule repérable.
1) Exprimer la pression différentielle 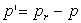 en fonction de (
en fonction de (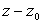 )
et de m, g, s, S
. )
et de m, g, s, S
.
2) Exprimer la sensibilité 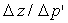
|
3) On incline le tube du manomètre, sa direction faisant
un angle a avec le plan horizontal. La position
du ménisque le long du tube est repérée par son abscisse
Z.
Calculer la nouvelle sensibilité.
8 - Un manomètre différentiel est constitué
de deux récipients cylindriques, de sections droites respectives  ,
reliés par un tube de section intérieure s constante.
,
reliés par un tube de section intérieure s constante.
A.N. 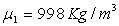 ;
; 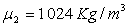 ;
; 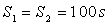
9 - Démontrer la loi de Laplace pour un goutte sphérique de liquide dans de l’air, pour une bulle de vapeur dans un liquide, pour une bulle de savon.
10 – Démontrer la loi de Jurin