Exercices sur les machines thermiques
Méthodologie
commune aux exercices ci-après
1 – A) Une centrale électrique fonctionne suivant
un cycle ditherme irréversible. La machine thermique entraîne un
turbo-alternateur produisant l’électricité et nous admettons que
la transformation travail-énergie électrique se fait avec des
pertes c’est à dire avec un rendement égal à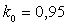 
.
Le rendement global de la centrale, défini par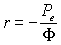 
où 
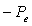est
la puissance électrique produite et 
l’énergie thermique fournie par le combustible " brûlé ",
peut s’écrire :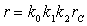 
- 
est le rendement
de la machine fonctionnant suivant un cycle de Carnot (ditherme réversible)
- 
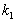un coefficient
tenant compte des pertes thermiques dans l’environnement défini par 
(
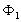est la puissance
calorifique cédée par la chaudière à la machine
thermique)
- 
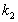un coefficient
tenant compte des irréversibilités défini par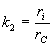 
(
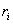est le rendement
réel de la machine thermique fonctionnant suivant le cycle ditherme irréversible)
A)1) La source chaude est à température 
,
la source froide à une température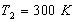 
.
Démontrer, à partir des premier et second principes de la Thermodynamique
que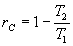 
; Application
numérique.
A)2) Pour un rendement global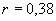 
, calculer la puissance électrique produite 
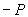si 
A)3) Les pertes thermiques sont de 15%, en déduire les valeurs numériques
de 
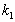et de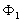 
.
A)4) Calculer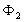 
puissance calorifique échangée avec la source froide.
A)5) Quelle est la valeur du rendement réel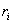 
de la machine thermique ? En déduire la valeur numérique
de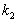 
.
B) On s’intéresse au fonctionnement d’une pompe à
chaleur fonctionnant suivant un cycle de Carnot entre les températures
Celsius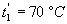 
et 
.
B)1) Expliquer, à partir d’un schéma, où l’on symbolisera
la pompe à chaleur et les sources de chaleur chaude et froide, les échanges
d’énergie à savoir les puissances calorifiques 
avec la source chaude,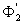 
avec la source froide et 
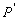le travail échangé par seconde.
B)2) Définir le coefficient de performance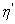 
et montrer qu’il est égal à 
.
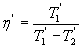B)3) La puissance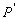 
est d’origine électrique. Pour une habitation dont le besoin en chauffage
est de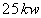 
, comparer
énergétiquement les 3 systèmes ci-après :
- chaudière à combustion d’un rendement égal à 0,9
- chauffage électrique à effet Joule avec la centrale étudiée
en A)
- pompe à chaleur avec la centrale étudiée en A)
| Réponse
A)1) | Réponse
A)2) | Réponse
A)3) | Réponse
A)4) | Réponse
A)5) | Réponse
B)1) | Réponse
B)2) | Réponse
B)3) |
2 - 1) Dans une centrale de production d’électricité, une
turbine à vapeur, actionnée par un moteur thermique, entraîne
le rotor de l’alternateur qui produit le champ magnétique tournant.
Dans ce moteur thermique, de l’eau décrit un cycle de transformations.
L’eau reçoit de la chaleur (le flux de chaleur est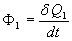 
)
d’une chaudière (source de chaleur) et fournit pendant l’unité
de temps le travail 
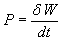à
la turbine.
1)1) Définir le rendement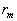 
du moteur thermique.
1)2) Montrer que l’on doit nécessairement disposer d’une source froide
pour réaliser un moteur (pour cela on écrira les premier et second
principes de la Thermodynamique pour un cycle avec une seule source de chaleur
et on démontrera que l’eau ne peut fournir du travail à la
turbine).
1)3) En écrivant les premier et second principes pour un cycle avec deux
sources de chaleur à températures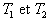 
(
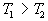), montrer que le
rendement du moteur est tel que :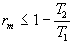
1)4) Est-il possible d’obtenir un rendement du moteur thermique égal à
1 même en l’absence de tout frottement et de toutes fuites thermiques ?
2) Dans la centrale nucléaire du Blayais, le long de
l’estuaire de la Garonne, l’eau de refroidissement prélevée dans
l’estuaire subit en circulant dans le condenseur une élévation
de 10°C (elle entre à 15°C et sort à 25°C).
Dans l’une des tranches, l’alternateur fournit la puissance électrique
. Les rendements
de l’alternateur et du moteur thermique actionnant la turbine sont respectivement
.
2)1) Expliquer le rôle du condenseur
2)2) Exprimer le flux de chaleur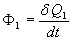 
en fonction de 
.
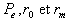En déduire que le flux de chaleur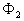 
fourni à l’eau de refroidissement est égal à 1684
MW.
2)3) Calculer le débit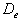 
en kg/s de l’eau de refroidissement (on rappelle la loi de calorimétrie
dans une transformation à pression constante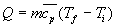 
;
la capacité calorifique massique de l’eau liquide est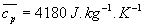 
).
3) Dans le condenseur, la vapeur d’eau à température
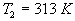est séparée
de l’eau de refroidissement (que, par simplification, nous prendrons uniforme
et égale à 
)
par une paroi d’épaisseur L répondant à l’hypothèse
de " mur thermique ".
| Réponse
1)1) | Réponse
1)2) | Réponse
1)3) | Réponse
1)4) | Réponse
2)1) | Réponse
2)2) | Réponse
2)3) | Réponse
3) |
3 - Soit une machine utilisant comme fluide l’air assimilé à
un gaz parfait diatomique.
3) Déduire de ces résultats le rendement thermodynamique du cycle de Stirling. Comparer ce rendement à celui que l’on obtiendrait si la machine fonctionnait selon le cycle de Carnot entre les mêmes sources aux températures T et T’. Expliquer la différence.
4) Comparer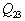 
et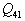 
. En déduire
un procédé original permettant d’obtenir le rendement maximal
du cycle de Carnot.
| Réponse
1) | Réponse
2) | Réponse
3) | Réponse
4) |
1) Les évolutions 1 ---> 2 et 3 ---> 4 étant
décrites de manière réversible, trouver une relation entre
, 
,
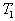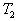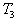et 
.
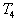Calculer 
et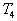 
.
2) Calculer pour une mole de gaz la quantité de chaleur
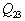échangée
ainsi que la variation d’entropie au cours de l’évolution 2 ---> 3.
3) Calculer le travail W échangé par une
mole au cours du cycle, en déduire le rendement de ce cycle. Comparer
ce rendement à celui qu’on obtiendrait si la machine fonctionnait selon
le cycle de Carnot entre les mêmes sources aux températures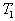
et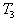 
.
Expliquer la différence.
| Réponse
1) | Réponse
2) | Réponse
3) |
5 - On se propose d’étudier le fonctionnement
et les performances d’une machine thermique (turbine à gaz à combustion
externe) dans laquelle un gaz que l’on supposera parfait décrit en circuit
fermé les opérations réversibles suivantes :
- le gaz initialement dans l’état (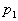
,
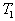) traverse un compresseur
dans lequel il subit une évolution adiabatique jusqu’à l’état
2 (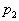
, 
),
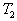- il se trouve alors en contact avec " une " source chaude
où il se réchauffe à pression constante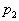
jusqu’à la température
,
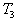il est alors dans l’état 3 (,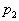
),
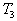- le gaz pénètre ensuite dans la turbine où il se détend
de manière adiabatique jusqu’à la pression ;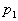
en fin de détente il est dans l’état 4 (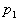
,
),
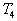- il achève de se refroidir à la pression ,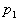
au contact " d’une " source froide jusqu’à la température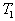
où il se trouve dans l’état 1.
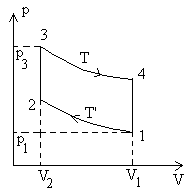
1) Tracer en diagramme p, V le cycle théorique
de cette machine et déterminer en fonction de,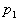
, 
,
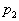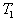les volumes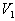 
,
, 
,
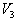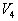d’une mole de
gaz dans les états 1, 2, 3, 4 ainsi que les températures 
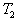et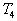 
.
2) Préciser les quantités de chaleur Q et q échangées par une mole de gaz avec les sources chaude et froide, ainsi que le travail global W de cette mole au cours du cycle.
3) Exprimer uniquement en fonction de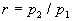 
le rendement théorique 
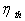de cette machine. Le rapport r étant imposé par les limites
de résistance de l’installation, avec lequel des trois gaz suivants obtiendra-t-on
le meilleur rendement ?
Argon g = 1,667; Air g
= 1,40; Dioxyde de Carbone g = 1,31
4) Préciser alors pour le gaz ainsi choisi et pour les
valeurs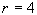 
, 
,
, 
,
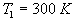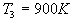les valeurs de,,
, ,
,,
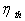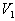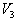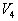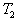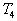et W.
5) Comparer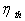
au rendement d’une machine fonctionnant selon le cycle de Carnot entre deux
sources aux températures uniformes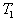
et .
| Réponse
1) | Réponse
2) | Réponse
3) | Réponse
4) | Réponse
5) |
6 - Etude théorique du fonctionnement d’une pompe à chaleur
On étudie le fonctionnement d’une pompe à chaleur
destinée au chauffage d’une habitation. l’appareil est une thermopompe
à compression utilisant comme vapeur condensable l’ammoniac (
)
de masse molaire 
.
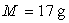Dans cette machine, le fluide pris à l’état gazeux sur la courbe
de rosée (vapeur saturante à pression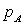 
et à température 
)
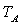est comprimé de manière adiabatique réversible jusqu’à
l’état B (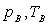
).
Il est ensuite refroidi puis entièrement liquéfié à
pression constante (état C correspondant au liquide saturant sur la courbe
d’ébullition, température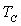 
)
dans un radiateur au contact de l’air de l’habitation qui constitue la source
chaude de la machine.
Il traverse alors un détendeur où il subit une détente
adiabatique réversible qui ramène sa pression de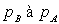 
.
Il se trouve alors partiellement liquéfié (état D).
Il pénètre ensuite dans l’évaporateur (source froide) et
se vaporise complètement à la pression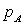
jusqu’au point A.
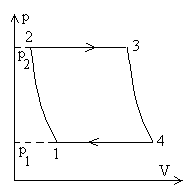
1) Représenter les différents éléments de la machine
thermique
2) Représenter sur un diagramme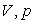 
le cycle de transformations décrit par le fluide ammoniac
3) Les données sont les suivantes :
Chaleur latente de vaporisation :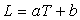 
avec 
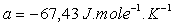et
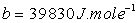
Calculer le débit d’ammoniac sachant que le maintien
de la température dans l’habitation nécessite une puissance de
chauffage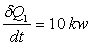 
.
Calculer l'entropie molaire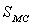 
.
En déduire le titre x de vapeur au point D si, pour le liquide
saturant à la pression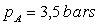 
,
l'entropie molaire est égale à 
.
Calculer la puissance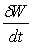 
échangée par le fluide.
En déduire le coefficient de performance de la pompe.
| Réponse
1) | Réponse
2) | Réponse
3) |
où
DT est l'écart de température
entre les deux faces du mur et S sa section transversale.
est
la conductivité thermique de la paroi et L = 0,15 m
son épaisseur, déduire la densité de flux de chaleur
traversant
la paroi et la surface d’échange nécessaire pour le flux
de chaleur 
et la température est 
.
A l’état 3, la pression est 
et la température est 
.
,
et 
et 
échangés
par une mole de gaz au cours du cycle ainsi que le travail W total.
.
Cette machine fonctionne selon le cycle de la figure ci-contre, dit cycle
de Joule composé de deux adiabatiques 1 ---> 2 et 3 --->
4 et de deux isobares 2 ---> 3 et 4 ---> 1 au cours desquelles le
gaz se met progressivement en équilibre de température avec
la source chaude à température 
ou la source froide à 
.
.
A l’état 3, la pression est 
et la température est 
.
;
; 
; 
; 
;
