L’indice M indique qu’une quantité est rapportée à une mole de matière (on dit molaire), la barre
CHAPITRE 8 : Détermination des fonctions d'état associées à un système homogène, sous une phase, en équilibre
Plan
1. Variables intensives et extensives
2. Travail des forces de pression extérieure
3. Expressions de la quantité de chaleur dQ
; coefficients calorimétriques
3.1. Relations entre les coefficients calorimétriques
3.2. Conséquences mathématiques des premier
et second principes
3.3. Détermination des fonctions d’état U,
H et S
3.4. Exemple de calcul des fonctions d'état
U, H et S : le gaz parfait
4. Mesure des capacités calorifiques
4.1. Méthodes de mesure pour les solides, les liquides
4.2. Méthodes de mesure pour les gaz
4.3. Résultats
Nous limitons nos propos aux variables d’état pression, volume, température et quantité de matière.
1. Variables intensives et extensives
Nous considérons un système S
homogène, sous une seule phase, en équilibre. Les variables
d’état y sont uniformes et constantes.
Elles sont liées par une équation d’état f(p, V,
T, n ou m) = 0.
Considérons une partie S’ de S
et notons que dans cette partie pression p et température T
sont inchangées alors que le volume est devenu l
V, la quantité de matière l
n ou l m où l
est compris entre 0 et 1.
Les variables d’état ont un caractère différent. On dira
que pression et température sont des variables intensives,
que volume et quantité de matière sont des variables extensives.
Ainsi si nous écrivons l’équation d’état pour S
sous la forme V = V(T, p, n ou m), elle s’écrira pour S’
l V= V(T, p, l n ou
l m) c’est à dire que la fonction V est une fonction
homogène de degré 1 en n ou en m.
La notation générale que nous utilisons est la
suivante : ![]()
L’indice
M indique qu’une quantité est rapportée à
une mole de matière (on dit molaire), la barre ![]() qu’elle est rapportée à l’unité de masse de matière
(on dit massique).
qu’elle est rapportée à l’unité de masse de matière
(on dit massique).
Nous avons noté le caractère additif des
fonctions d’état U et S.
Pour un système homogène, sous une phase, en équilibre
ces fonctions seront extensives (![]() ).
Il en sera, de même, de la fonction d’état enthalpie
).
Il en sera, de même, de la fonction d’état enthalpie ![]() ,
la quantité pV produit d’une variable intensive par une variable
extensive étant extensive.
,
la quantité pV produit d’une variable intensive par une variable
extensive étant extensive.
2. Travail des forces de pression extérieure
Le piston (paroi mobile en translation) est la technologie la plus simple pour aborder l’échange d’énergie par travail provoquant un changement de l’état interne du système. Les études de technologies liées à des roues mobiles (turbines) sont plus complexes et ne sont pas envisagées dans le cadre de ce cours.
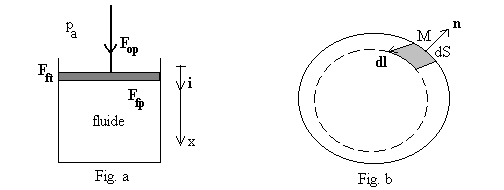
Fig. a - Nous raisonnons sur un piston plan de section S dont le déplacement est suivant la direction verticale x. Ce cas particulier n’enlève rien à la généralité de nos propos.
Il est soumis à la force de l’opérateur extérieur
de composante verticale ![]() ,
à son poids
,
à son poids ![]() ,
à la pression de l’environnement
,
à la pression de l’environnement ![]() ,
à la force tangentielle de frottement de contact
,
à la force tangentielle de frottement de contact ![]() (seule la projection tangentielle travaille) et à la force
(seule la projection tangentielle travaille) et à la force ![]() qu’exerce le système fluide sur le piston (
qu’exerce le système fluide sur le piston (![]() est la force exercée par le piston sur le fluide).
est la force exercée par le piston sur le fluide).
Nous cherchons à connaître le travail dW
échangé par le système fluide du à l’action du piston,
soit ![]() où
où
![]() est le vecteur
déplacement élémentaire du piston.
est le vecteur
déplacement élémentaire du piston.
L’application du théorème de l’énergie
cinétique au piston permet d’écrire : ![]()
Pour le travail de la force de frottement, il s’agit de la
vitesse de glissement du piston sur la paroi du cylindre qui, ici , se confond
avec la vitesse v du piston puisque le mouvement est une translation.
La pression extérieure est définie par la relation ![]() si bien que le travail échangé s’écrit
si bien que le travail échangé s’écrit ![]() où nous avons introduit
où nous avons introduit ![]() variation de volume du système fluide (pour un déplacement du
piston positif, nous avons une diminution de volume du système ce qui
explique l’origine du signe moins).
variation de volume du système fluide (pour un déplacement du
piston positif, nous avons une diminution de volume du système ce qui
explique l’origine du signe moins).
L’expression de d W est, même pour ce
cas simplifié, difficilement manipulable car il nous faut connaître
le problème mécanique.
Aussi nous envisageons d W
alors le travail échangé est égal à
![]()
Fig. b - Dans le cas général, le calcul
doit être fait à chaque élément de surface dS
sans faire d’hypothèse sur les directions des forces ou des déplacements.
La pression extérieure ![]() au
point M doit être comprise comme la somme de la pression d’environnement
au
point M doit être comprise comme la somme de la pression d’environnement
![]() et des projections,
suivant la normale à l’élément de surface, des forces extérieures
(force d’opérateur et poids). Alors
et des projections,
suivant la normale à l’élément de surface, des forces extérieures
(force d’opérateur et poids). Alors ![]()
(en
négligeant le travail des forces de frottement de contact et l’énergie
cinétique de l’élément de surface)
Remarque : si ![]() ,
le travail est moteur (le système " pousse "
sur le milieu extérieur) ; il est récepteur dans le cas
opposé.
,
le travail est moteur (le système " pousse "
sur le milieu extérieur) ; il est récepteur dans le cas
opposé.
Cas d’une pression extérieure uniforme
Dans ce cas là, entre deux instants successifs, nous
pouvons intégrer l’expression de ![]() à tous les éléments de surface.
à tous les éléments de surface.
![]() où dV est la variation de volume du système.
où dV est la variation de volume du système.
Cas d’une transformation quasistatique, d’une transformation réversible
Le système est en état d’équilibre ou
très voisin d’un état d’équilibre. Les vitesses de déplacement
ou de glissement sont " nulles ".
La pression du système est uniforme et égale à p.
En écrivant le principe fondamental de la dynamique sur chaque élément
de surface, on obtient :
![]() (transformation réversible ; cette condition traduit aussi la condition
d’équilibre mécanique sur une paroi mobile)
(transformation réversible ; cette condition traduit aussi la condition
d’équilibre mécanique sur une paroi mobile)
![]() (transformation quasistatique)
(transformation quasistatique)
Le travail échangé devient égal à
![]()
Représentation du travail dans un diagramme V, p
|
|
Cas d’un cycle : W > 0 si le cycle est décrit dans le sens trigonométrique (ou positif) W < 0 si le cycle est décrit dans le sens inverse (ou négatif). W > 0 le système est une machine réceptrice W < 0 le système est une machine motrice |
Ces schémas montrent que le travail des forces de pression extérieure dépend des états initial et final, des états intermédiaires c’est à dire de la transformation amenant de l’état initial à l’état final (on dit du chemin suivi).
3. Expressions de la quantité de chaleur dQ ; coefficients calorimétriques
Les premier et second principes permettent d’écrire :
![]() et
et ![]() .
.
U (ou ![]() )
et S sont des fonctions des variables d’état. Par suite, pour
une quantité donnée de matière et suivant le couple de
variables indépendantes choisies, on obtient trois expressions équivalentes
pour
)
et S sont des fonctions des variables d’état. Par suite, pour
une quantité donnée de matière et suivant le couple de
variables indépendantes choisies, on obtient trois expressions équivalentes
pour ![]() .
.
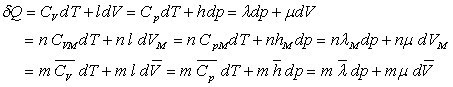 où CV, Cp,
l, h, l et m
sont appelés coefficients calorimétriques.
où CV, Cp,
l, h, l et m
sont appelés coefficients calorimétriques.
CV et Cp
ont un nom propre : respectivement, capacités calorifiques à volume
constant et à pression constante.
Pour ![]() , on ajoute
le mot molaire à la nomination ; pour
, on ajoute
le mot molaire à la nomination ; pour ![]() ,
on ajoute le mot massique à la nomination.
,
on ajoute le mot massique à la nomination.
CV, Cp, h et l ont un caractère extensif, les coefficients l et m sont intensifs.
![]() ;
; ![]() ;
; ![]() ;
; ![]()
Remarques :
3.1. Relations entre les coefficients calorimétriques
Par exemple, ![]()
En reportant dans la première expression de dQ
et en identifiant avec la troisième, on obtient les relations ![]()
Il est possible de recommencer la procédure autant de fois que l’on peut et de trouver autant de couple de relations entre les coefficients calorimétriques.
Dans l’encadré ci-dessous, nous avons indiqué les relations utiles entre les coefficients calorimétriques et conseillons au lecteur de savoir les retrouver.
![]() ;
; ![]() ;
; ![]()
L’outil mathématique nécessaire à ce cours
de Thermodynamique (calcul différentiel) n’est pas difficile : pratiqué
de manière systématique, il demande un peu d'entraînement.
Le lecteur pourra utiliser, avec profit l’annexe " Outils de calcul
pour Sciences physiques ".
3.2. Conséquences mathématiques des premier et second principes
Variables d’état indépendantes T, V
![]()
Les deux différentielles totales exactes obéissent à la relation de Cauchy.
![]()
![]()
Par identification et dérivation, on obtient :
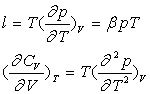
Variables d’état indépendantes T, p
![]()
Les deux différentielles totales exactes obéissent à la relation de Cauchy.
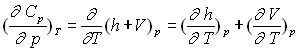
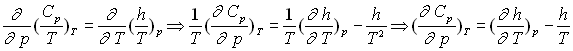
Par identification et dérivation, on obtient :
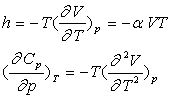
Remarques
3.3. Détermination des fonctions d’état U, H et S
En remplaçant l ou h dans la relation
entre coefficients calorimétriques ![]() et en utilisant la relation entre
et en utilisant la relation entre ![]() , on obtient :
, on obtient :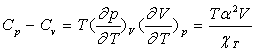
Le coefficient de compressibilité isotherme ![]() est, pour tous les corps, positif ce qui fait que la capacité calorifique
à pression constante est toujours supérieure à la capacité
calorifique à volume constant.
est, pour tous les corps, positif ce qui fait que la capacité calorifique
à pression constante est toujours supérieure à la capacité
calorifique à volume constant.
Si l’équation d’état est connue, les coefficients
calorimétriques l et h sont connus, la différence
![]() est connue, les
coefficients l et m
sont connus si
est connue, les
coefficients l et m
sont connus si ![]() le sont.
le sont.
3.4. Exemple de calcul des fonctions d'état U, H et S : le gaz parfait
La méthode est transposable à toute matière dont on a déterminé l’équation d’état et dont on a des renseignements sur l’une des capacités calorifiques.
Coefficients calorimétriques
![]()
![]() ;
; ![]()
![]()
![]() ;
;
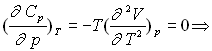
![]()
|
|
Ce résultat est connu sous le nom de relation de Mayer |
Tous ces résultats théoriques sont conformes aux mesures présentées dans le tableau de résultats du paragraphe 4.
L’introduction de ![]()
![]() ;
; 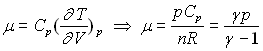
Fonctions d’état U, H et S
Energie interne
![]()
L’énergie interne d’un gaz parfait ne dépend que de la température.
Un gaz dont l’énergie interne ne dépend que de la température obéit à la première loi de Joule
Ce résultat peut être validé par l’expérience
appelée détente de Joule-Gay Lussac.
Pour un gaz monoatomique, ![]() est
constant et égal à
est
constant et égal à ![]() ,
sauf à des températures très voisines de 0 K où
,
sauf à des températures très voisines de 0 K où
![]() varie rapidement.
varie rapidement.
![]()
Pour un diatomique, ![]() varie rapidement dans certaines plages de température, en dehors de ces
domaines il est à peu près constant ð
varie rapidement dans certaines plages de température, en dehors de ces
domaines il est à peu près constant ð
![]()
Aux températures
ordinaires ![]()
![]()
On se reportera au paragraphe 4 pour les résultats
expérimentaux et leurs interprétations des ![]() des gaz parfaits.
des gaz parfaits.
Enthalpie
![]()
L’enthalpie d’un gaz parfait ne dépend que de la température.
Un gaz dont l’enthalpie ne dépend que de la température obéit à la deuxième loi de Joule
Ce résultat peut être validé par l’expérience appelée détente de Joule-Thomson.
Remarque 1 : On sait que les valeurs de H se déduisent directement des valeurs de U (et inversement) à partir de la définition.
H = U + pV = U + nRT.
Or ![]() et
on retrouve
et
on retrouve ![]()
Remarque 2 : un gaz obéissant aux deux lois de Joule est un gaz parfait
Le gaz obéit à la première loi de Joule
![]()
à ![]()
Le gaz obéit à la deuxième loi de Joule
![]()
à ![]()
En rapprochant les deux résultats, on obtient ![]()
Soit ![]() .
En remplaçant y ou j
par sa valeur, il vient pV=KT qui est l’équation d’état
des gaz parfaits.
.
En remplaçant y ou j
par sa valeur, il vient pV=KT qui est l’équation d’état
des gaz parfaits.
Un gaz qui obéit aux deux lois de Joule est un gaz parfait.
Entropie
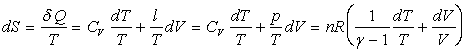
En utilisant les couples de variables indépendantes T, p ou p, V on obtient des relations similaires.

Dans des domaines de température où g est constant (c’est à dire où CV et Cp sont constants) l’intégration des formules de dS ne présente guère de difficulté.
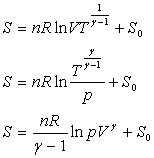
4. Mesure des capacités calorifiques
4.1. Méthodes de mesure pour les solides, les liquides
En réalisant une transformation isobare, on détermine
expérimentalement Cp . On calcule
CV à partir de ![]() .
.
En fait les écarts relatifs ![]() restent faibles, 5% pour l’aluminium, 4% pour l’or, 3% pour le cuivre et l’argent,
... de l’ordre de grandeur des erreurs de mesures.
restent faibles, 5% pour l’aluminium, 4% pour l’or, 3% pour le cuivre et l’argent,
... de l’ordre de grandeur des erreurs de mesures.
La méthode des mélanges
|
|
Un vase est rendu pratiquement adiabatique par une enveloppe
isolante (ou un système d’isolation complexe). Un tel système
est appelé calorimètre adiabatique. On y introduit
une masse d’eau de capacité calorifique massique à pression
constante |
On agite afin d’atteindre un équilibre à température
finale ![]() au plus
vite.
au plus
vite.
Soit m la masse d’eau qui échangerait
d’un point de vue thermique comme le vase et les accessoires (agitateur, capteur
de température).
La transformation est irréversible, isobare à la pression ![]() de l’environnement (le plus souvent,
de l’environnement (le plus souvent, ![]() ).
).![]()
Pour le système, corps solide + calorimètre,
la quantité de chaleur, donc la variation d’enthalpie, est nulle.
![]()
L’enthalpie est une fonction d’état, sa variation ne
dépend que des états initial et final.
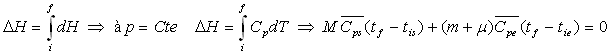
soit 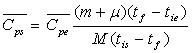
Cette méthode nécessite la mesure préalable de m qui pourra être faite par la méthode électrique exposée ci-après ou en faisant une expérience préalable avec une masse m’ d’eau à température connue à la place du solide.
La méthode électrique
Particulièrement adaptée pour les liquides, elle
consiste à chauffer le liquide enfermé dans le calorimètre
adiabatique à l’aide d’une résistance électrique. La connaissance
de l’énergie électrique fournie et de l’élévation
de température permet la mesure de la capacité calorifique.
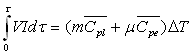
V : tension aux bornes de la résistance ; I : courant électrique
; m : masse du liquide ; ![]() capacité calorifique massique à pression constante du liquide
; m : valeur en eau du calorimètre;
capacité calorifique massique à pression constante du liquide
; m : valeur en eau du calorimètre;
![]() : capacité calorifique massique
à pression constante de l’eau ; DT
: élévation de température.
: capacité calorifique massique
à pression constante de l’eau ; DT
: élévation de température.
Remarques :
4.2. Méthodes de mesure pour les gaz
Ces mesures sont difficiles en raison de la faiblesse des masses volumiques des gaz et donc des capacités calorifiques.
On mesure ![]() et l’on déduit
et l’on déduit ![]() soit de la formule
soit de la formule ![]() ,
soit de la mesure de
,
soit de la mesure de ![]() .
.
Dans le cadre des expériences de cours, nous étudierons
deux méthodes :
- celle connue sous le nom de méthode du courant stationnaire
(mesure de ![]() ;
cette méthode peut être employée pour les liquides),
;
cette méthode peut être employée pour les liquides),
- celle connue sous le nom d’expérience de Clément et Desormes
(mesure de g).
Un autre processus de mesure de g
porte le nom de formule de Reech.
Nous avons introduit le coefficient de compressibilité isotherme ![]() ,
nous introduisons celui de compressibilité adiabatique
,
nous introduisons celui de compressibilité adiabatique ![]() et remarquons que
et remarquons que 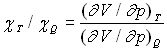 en un même état.
en un même état.
![]()
![]()
Ainsi ![]()
|
|
Traçons dans un diagramme V, p (diagramme
de Clapeyron) l’isotherme passant par le point A0
de coordonnées (p0 , V0).
Les dérivées En un même point, la pente de l’adiabatique, dans un diagramme V, p, est toujours plus accentuée que celle de l’isotherme. |
Cas des gaz
Le tableau ci-après et les courbes représentées rassemblent les principaux résultats.
|
CpM pour 1 atmosphère |
CVM pour |
g = |
|||||||||||||
|
300 K |
600 K |
1200 K |
1800 K |
1 atm, 300 K |
CpM - CVM |
CpM / CVM |
|||||||||
|
Gaz monoato He |
20,6 |
20,6 |
20,6 |
20,7 |
12,5 |
8,11 |
~5/3 |
||||||||
|
miques Ar |
20,8 |
20,8 |
20,9 |
20,9 |
12,5 |
8,32 |
~5/3 |
||||||||
|
Gaz diato O2 |
29,3 |
32,1 |
35,7 |
37,3 |
21,0 |
8,32 |
~1,4 |
||||||||
|
miques N2 |
29,1 |
30,3 |
33,7 |
35,6 |
20,7 |
8,36 |
~1,4 |
||||||||
|
H2 |
28,8 |
29,3 |
31,0 |
33,5 |
20,4 |
8,40 |
~1,4 |
||||||||
|
Autres gaz H2O |
36,3 |
42,2 |
49,7 |
||||||||||||
|
CO2 |
37,1 |
47,2 |
56,4 |
59,8 |
28,4 |
8,65 |
~1,3 |
||||||||
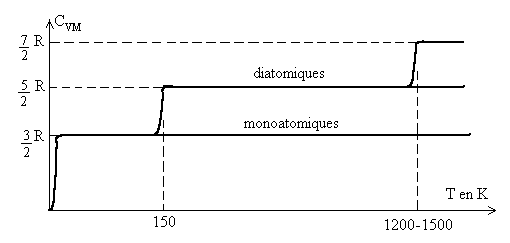
Commentaires : Les résultats sont donnés pour une pression atmosphérique normale pour laquelle, en première approximation, les gaz réels ont un comportement de gaz parfait.
Les courbes traduisent les évolutions de ![]() avec la température, des différences apparaissent avec l’atomicité.
avec la température, des différences apparaissent avec l’atomicité.
La valeur de ![]() est égale à R quelque soit le gaz.
est égale à R quelque soit le gaz.
A la température T = 0 K, la valeur de ![]() est nulle. Elle évolue très rapidement (entre 0 et 2-3K)
vers la valeur
est nulle. Elle évolue très rapidement (entre 0 et 2-3K)
vers la valeur ![]() quelque soit le gaz.
quelque soit le gaz.
Les gaz monoatomiques gardent cette dernière valeur quelque soit la température.
Ce résultat est conforme au principe d'équipartition de l'énergie
et à l'affectation d'une énergie égale à ![]() par possibilité d'énergie et par particule (pour un atome, le
mouvement général de translation -superposition dans l'espace
euclidien de trois translations indépendantes- correspond à trois
possibilités d'énergie). En ce qui concerne l'évolution
entre 0 et 2-3K, il faut admettre que les atomes se mettent en mouvement
progressivement lorsque la température augmente (Mécanique quantique).
par possibilité d'énergie et par particule (pour un atome, le
mouvement général de translation -superposition dans l'espace
euclidien de trois translations indépendantes- correspond à trois
possibilités d'énergie). En ce qui concerne l'évolution
entre 0 et 2-3K, il faut admettre que les atomes se mettent en mouvement
progressivement lorsque la température augmente (Mécanique quantique).
Les autres gaz subissent deux évolutions pour ![]() ,
l’une autour de 150 K, l’autre autour de 1200-1500 K.
,
l’une autour de 150 K, l’autre autour de 1200-1500 K.
Pour les diatomiques, ![]() atteint la valeur
atteint la valeur ![]() ,
puis
,
puis ![]() . Pour une
atomicité supérieure, les résultats sont plus complexes.
Ils dépendent de la forme de la molécule et de son atomicité.
On atteint d’abord
. Pour une
atomicité supérieure, les résultats sont plus complexes.
Ils dépendent de la forme de la molécule et de son atomicité.
On atteint d’abord ![]() ,
puis une valeur plus élevée.
,
puis une valeur plus élevée.
Pour interpréter ces résultats, il faut envisager
des possibilités d'énergie supplémentaires.
Dans le cas de la transition autour de 150 K, les molécules entrent
progressivement à ce niveau de température en rotation. Si on
considère une molécule diatomique, il y aura deux possibilités
nouvelles d'énergie (ð ![]() par molécule), la rotation autour de l'axe joignant les atomes n'est
pas à considérer ; pour les polyatomiques, il y a trois possibilités
d'énergie sauf dans le cas de certaines molécules triatomiques
de type
par molécule), la rotation autour de l'axe joignant les atomes n'est
pas à considérer ; pour les polyatomiques, il y a trois possibilités
d'énergie sauf dans le cas de certaines molécules triatomiques
de type ![]() qui sont
géométriquement linéaires.
qui sont
géométriquement linéaires.
Dans le cas de la transition autour 1200-1500 K, les possibilités
supplémentaires d'énergie sont fournies par la vibration, à
l'intérieur des molécules, des atomes les uns par rapport aux
autres ; une vibration correspond à deux possibilités d'énergie
(cinétique et potentielle). Le nombre de vibrations possibles pour une
molécule est égale à : ![]() si A est l'atomicité et r le nombre de rotation à
considérer.
si A est l'atomicité et r le nombre de rotation à
considérer.
Cas des solides
Le tableau ci-dessous donne la capacité calorifique massique et molaire à pression constante pour différents corps simples à température et pression ordinaires ainsi que les masses molaires M.
|
Be |
B |
C |
Al |
P |
Fe |
Cu |
Ag |
Sb |
Pb |
|
|
diamant |
blanc |
|||||||||
|
M en g |
9 |
10,8 |
12 |
27 |
31 |
55,8 |
63,5 |
108 |
122 |
207 |
|
|
1,63 |
1,0 |
0,50 |
0,88 |
0,79 |
0,46 |
0,39 |
0,23 |
0,21 |
0,13 |
|
|
14,7 |
10,8 |
6,0 |
23,7 |
24,6 |
25,6 |
24,7 |
24,8 |
25,5 |
26,8 |
On constate, sauf pour les éléments légers
tels que Be, B et C, que la capacité calorifique molaire est à
peu près ![]() (loi de Dulong et Petit).
(loi de Dulong et Petit).
|
|
En fait Si la température est suffisante, |
Ces résultats sont conformes avec le principe d'équipartition de l'énergie, chaque atome du cristal ayant comme possibilités d'énergie des vibrations dans les trois directions de l'espace euclidien.
|
|
Certaines substances solides présentent plusieurs
structures cristallines (on dit aussi plusieurs variétés
allotropiques) et, à l’intérieur de l’état solide,
il y a changement de phase ou d’état. |
Cas des liquides
|
|
Il n’y a pas de loi simple. Pour de nombreux liquides,
on trouve un |