L'air au dessus de 200 K est donc un gaz (sa température critique est inférieure à 200 K ; en fait la température critique de l'air est 132,4 K).
Une pression de
A)1) L'équation d'état donnée est celle du gaz
parfait, limite de comportement de tous les gaz réels lorsque la pression
devient nulle.
L'air au dessus de 200 K est donc un gaz (sa température critique
est inférieure à 200 K ; en fait la température
critique de l'air est 132,4 K).
Une pression de ![]() doit être considérée comme une pression relativement faible
puisqu'on peut appliquer l'équation d'état des gaz parfaits.
doit être considérée comme une pression relativement faible
puisqu'on peut appliquer l'équation d'état des gaz parfaits.
A)2) ![]() peut aussi s'écrire
peut aussi s'écrire ![]() ,
soit encore
,
soit encore ![]() puisque
pour un gaz parfait
puisque
pour un gaz parfait ![]() .
.
![]() correspond à
5 degrés de liberté soit, dans le cas des molécules diatomiques
(cas de l'air) aux températures comprises entre 150 K et 1200
K, à 3 degrés de liberté pour le mouvement de translation
du centre de masse et à 2 degrés de liberté pour les deux
rotations possibles.
correspond à
5 degrés de liberté soit, dans le cas des molécules diatomiques
(cas de l'air) aux températures comprises entre 150 K et 1200
K, à 3 degrés de liberté pour le mouvement de translation
du centre de masse et à 2 degrés de liberté pour les deux
rotations possibles.
![]() ð
ð ![]()
![]() ð
ð ![]()
A)3) ![]() ð
ð ![]()
![]()
B)1) ![]() ð
ð ![]()
B)2)a) ![]()
B)2)b) ![]() et
et ![]() (transformation
isotherme d'un gaz parfait)
(transformation
isotherme d'un gaz parfait)
B)2)c) 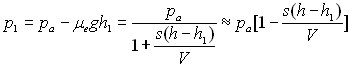
Soit ![]() ð
ð
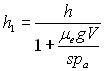
A.N. ![]()
B)3)a) Transformation adiabatique réversible
pour un gaz parfait tel que ![]()
![]() ð
ð 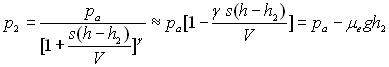
Soit ![]() ð
ð

A.N. ![]()
B)4) Cette expérience peut être exploitée
pour mesurer le rapport g .
L'expérience de Clément et Desormes.
Dans une bonbonne de gaz, on crée une surpression faible mesurée
par un manomètre. On supprime la suppression en établissant un
contact rapide avec l'extérieur (détente adiabatique quasi-statique)
puis on attend que le gaz de la bonbonne retrouve un équilibre thermique
avec l'extérieur ce qui crée une nouvelle surpression (transformation
à volume constant).
L'étude théorique des deux transformations permet de connaître
le rapport g par la mesure de la surpression
initiale et de la surpression finale.
C)1) Le coup de pompe consiste à introduire une quantité supplémentaire Dn d'air dans le compartiment B qui en contient n.
![]() ;
; ![]() ;
; ![]()
Soit
![]()
C)2) Il s'agit de calculer le travail pour une compression
isotherme réversible de ![]() moles de gaz parfait à température
moles de gaz parfait à température ![]() de la pression
de la pression ![]() .
.
![]() ð
ð
![]()
C)3) La variation d'énergie interne est due à
l'augmentation du nombre de moles de gaz parfait (la température restant
constante)
![]()
C)4) L'apport
en moles de gaz parfait au 2ème coup de pompe est : ![]()
La pression sera : ![]()
Ainsi ![]() ;
; ![]() ;
; ![]() et, à
partir d'un raisonnement par récurrence
et, à
partir d'un raisonnement par récurrence ![]()
Application : ![]() ð
ð ![]()