U (ou
CHAPITRE 7 : Propriétés de la matière
Plan
Les caractéristiques thermodynamiques des corps
homogènes
1. Expressions de la quantité de chaleur dQ
; coefficients calorimétriques
2. Conséquences mathématiques des premier
et second principes
3. Détermination des fonctions d’état
3.1. Tables de données thermodynamiques
3.2. Exemple : le gaz parfait
Etude thermodynamique des changements de phase
1. Etude énergétique des vapeurs saturantes
2. Relations de Clapeyron
Les caractéristiques thermodynamiques des corps homogènes
Ces corps obéissent à une équation d’état
f(p,
V, T, n ou m) = 0.
Pour un système fermé, la quantité de matière
est fixée et ne doit pas être considérée comme
une variable d’état.
Le nombre de variables d’état indépendantes pour ces
systèmes est égal à deux et l’équation d’état
peut être écrite :
V = V(T, p) ou p = p(T, V) ou T = T(p, V) qui
veut dire, par exemple, que le volume V est une fonction des variables
indépendantes T et p.
Les fonctions d’état U, H et S seront des fonctions
de deux variables d’état indépendantes.
L’outil mathématique nécessaire à la Thermodynamique
repose sur le calcul différentiel. Il n’est pas difficile en soi,
il exige de la méthodologie c’est à dire un entraînement
obligé.
Le lecteur pourra utiliser l’annexe " Eléments de Mathématiques
" avec profit.
1. Expressions de la quantité de chaleurdQ ; coefficients calorimétriques
Les premier et second principes permettent d’écrire ![]() et
et ![]()
U (ou ![]() )
et S sont des fonctions des variables d’état. Par suite, suivant
le couple de variables indépendantes choisies, on obtient trois expressions
équivalentes pour
)
et S sont des fonctions des variables d’état. Par suite, suivant
le couple de variables indépendantes choisies, on obtient trois expressions
équivalentes pour ![]() .
.
![]() où CV,
Cp, l, h, let
m sont appelés coefficients calorimétriques.
où CV,
Cp, l, h, let
m sont appelés coefficients calorimétriques.
Dans le chapitre 4, nous avons introduit CVet
Cp avec le nom propre de, respectivement,
capacités calorifiques à volume constant et à pression
constante.
Pour un système homogène, nous avons noté dans
ce chapitre que
dQ avait un caractère
extensif si bien que, compte tenu du caractère intensif de T
et p, du caractère extensif de V, les coefficients
CV,
Cp, h et lsont
extensifs, les coefficients l et
m
sont intensifs.
![]() ;
; ![]() ;
; ![]() ;
; ![]()
![]() , qui sont respectivement
les capacités calorifiques massiques à volume constant et à
pression constante sont, aussi appelées chaleurs spécifiques à
volume constant et à pression constante.
, qui sont respectivement
les capacités calorifiques massiques à volume constant et à
pression constante sont, aussi appelées chaleurs spécifiques à
volume constant et à pression constante.
Remarques :
- le symbole ![]() représente un coefficient calorimétrique dans les expressions
ci-dessus et la conductivité thermique dans la loi de Fourier,
représente un coefficient calorimétrique dans les expressions
ci-dessus et la conductivité thermique dans la loi de Fourier,
- l’unité de mesure de ces différents coefficients calorimétriques
se détermine, sans difficulté, à partir de l’analyse
dimensionnelle (équations aux dimensions) ; ainsi, par exemple,
l se mesure dans le système MKSA en J/m3.
Relations entre les coefficients calorimétriques
Par exemple, ![]() en reportant dans la première expression de dQ
et en identifiant avec la troisième, on obtient les relations
en reportant dans la première expression de dQ
et en identifiant avec la troisième, on obtient les relations ![]()
Il est possible de recommencer la procédure autant de fois que l’on peut et de trouver autant de couple de relations entre les coefficients calorimétriques.
Ci-dessous, nous avons indiqué les relations utiles entre les coefficients calorimétriques et conseillons au lecteur de savoir les retrouver.
![]() ;
;
![]() ;
;
![]()
Coefficients thermoélastiques
Ces coefficients (déterminés expérimentalement et que l’on trouve dans les livres de données thermodynamiques) permettent d’établir les équations d’état.
![]() coefficient
de dilatation à pression constante
coefficient
de dilatation à pression constante
![]() coefficient
d’augmentation de pression à volume constant
coefficient
d’augmentation de pression à volume constant
![]() coefficient
de compressibilité isotherme
coefficient
de compressibilité isotherme
La relation mathématique ![]()
La dérivation de l’équation d’état donne les coefficients
thermoélastiques, l’intégration de deux des coefficients
thermoélastiques fournit l’équation d’état.
Le lecteur trouvera sans difficulté que, pour un gaz parfait, ![]()
2. Conséquences mathématiques des premier et second principes
Variables d’état indépendantes T, V
![]()
Les deux différentielles totales exactes obéissent à la relation de Cauchy.
![]()
![]()
Par identification et dérivation, on obtient : 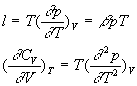
Variables d’état indépendantes T, p
![]()
Les deux différentielles totales exactes obéissent à la
relation de Cauchy et on obtient : 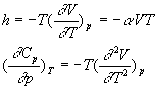
Remarques
- avec les variables T, V on utilise les fonctions énergie
interne U et entropie S ; avec les variables T, p
il convient d’utiliser les fonctions enthalpie H et entropie S,
- les variables p, V sont d’un emploi plus difficile parce que
la variable T apparaît explicitement dans l’expression de
dS,
- à partir des expressions des différentielles de dU et
dH, on retrouve (chapitre 4) ![]() et
et ![]()
3. Détermination des fonctions d’état U, H et S
3.1. Tables de données thermodynamiques
En remplaçant l ou h dans la relation entre coefficients
calorimétriques ![]() et en utilisant la relation entre
et en utilisant la relation entre ![]() , on obtient :
, on obtient :
![]()
Le coefficient de compressibilité isotherme ![]() est, pour tous les corps, positif ce qui fait que la capacité calorifique
à pression constante est toujours supérieure à la capacité
calorifique à volume constant.
est, pour tous les corps, positif ce qui fait que la capacité calorifique
à pression constante est toujours supérieure à la capacité
calorifique à volume constant.
Si l’équation d’état est connue, les coefficients calorimétriques
l et h sont connus, la différence![]() est connue, les coefficients l et m
sont connus si
est connue, les coefficients l et m
sont connus si ![]() le sont.
le sont.
Du point de vue de la Thermodynamique, la caractérisation d’un corps homogène nécessite la détermination expérimentale d’un coefficient calorimétrique soit CV soit Cp (en fait Cp ) et de l’équation d’état (ou des coefficients thermoélastiques).
On trouvera, dans ce document, une annexe intitulée "Détermination expérimentale des caractéristiques thermodynamiques " qui traite de la détermination expérimentale des équations d’état (ou des coefficients thermoélastiques), de la calorimétrie dont l’objet est la mesure des capacité calorifiques et des chaleurs latentes
Les différentielles dU ( ou dH ), dS sont
connues, les fonctions U (ou H ), S aussi à
une constante additive près.
En ce qui concerne l’entropie, le troisième principe de la Thermodynamique
(appelé postulat de Nernst-Planck) précise que l’entropie
est nulle à 0 K.
Pour ce qui est de l’énergie interne ou de l’enthalpie, on définit
un état de référence appelé état standard
qui pour les corps purs correspond à la pression standard ![]() ,
la température étant à préciser (souvent on utilise
la température 25 °C).
,
la température étant à préciser (souvent on utilise
la température 25 °C).
Tout ceci permet de constituer ce qu’il est convenu d’appeler les tables
thermodynamiques, très utilisées par les thermochimistes
et par les ingénieurs thermodynamiciens.
La méthode est applicable, sans hésitation, à toute matière dont on a déterminé l’équation d’état et dont on a des renseignements sur l’une des capacités calorifiques. Nous conseillons vivement au lecteur les exercices notés de 1 à 10.
Coefficients calorimétriques
![]()
![]()
![]()
![]()
![]() ;
; ![]()
![]()
| Ce résultat est connu sous le nom de relation de Mayer |
Tous ces résultats théoriques sont conformes aux
mesures présentées dans le tableau de résultats de
l’annexe.
L’introduction de ![]()
![]() ;
; ![]()
Fonctions d’état U, H et S
Energie interne
![]()
L’énergie interne d’un gaz parfait ne dépend que de la
température.
Un gaz dont l’énergie interne ne dépend que de la température
obéit à la première loi de Joule.
Ce résultat peut être validé par l’expérience
appelée détente de Joule-Gay Lussac.
Pour un gaz monoatomique, ![]() est
constant et égal à
est
constant et égal à ![]() ,
sauf à des températures très voisines de 0 K où
,
sauf à des températures très voisines de 0 K où ![]() varie
rapidement.
varie
rapidement.
![]()
Pour un diatomique, ![]() varie rapidement dans certaines plages de température, en dehors de ces
domaines il est à peu près constant ð
varie rapidement dans certaines plages de température, en dehors de ces
domaines il est à peu près constant ð![]()
Aux températures ordinaires ![]()
![]()
Enthalpie
![]()
L’enthalpie d’un gaz parfait ne dépend que de la température.
Un gaz dont l’enthalpie ne dépend que de la température
obéit à la deuxième loi de Joule.
Ce résultat peut être validé par l’expérience
appelée détente de Joule-Thomson.
Remarque 1 : On sait que les valeurs de H se déduisent
directement des valeurs de U (et inversement) à partir de
la définition.
H = U + pV = U + nRT.
Or![]() et on retrouve
et on retrouve ![]()
Remarque 2 : un gaz obéissant aux deux lois de Joule est
un gaz parfait.
Le gaz obéit à la première loi de Joule ![]()
à ![]()
Le gaz obéit à la deuxième loi de Joule ![]()
à ![]()
En rapprochant les deux résultats, on obtient ![]()
Soit ![]() . En
remplaçant y ou j
par sa valeur, il vient pV=KT qui est l’équation d’état
des gaz parfaits.
. En
remplaçant y ou j
par sa valeur, il vient pV=KT qui est l’équation d’état
des gaz parfaits.
Un gaz qui obéit aux deux lois de Joule est un gaz parfait.
Entropie
![]()
En utilisant les couples de variables indépendantes T, p
ou p, V on obtient des relations similaires.
![]()
Dans des domaines de température où g
est constant (c’est à dire où CV
et Cp sont constants) l’intégration
des formules de dS ne présente guère de difficulté.
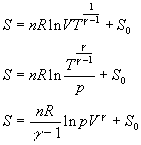
Etude thermodynamique des changements
de phase
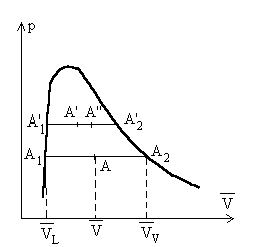 |
Nous raisonnons sur une unité de masse
de corps pur et considérons les deux paliers de liquéfaction
A1A2 et
A’1A’2
à température T et T + dT.
On appelle x le titre de vapeur saturante défini comme étant la proportion en masse de vapeur dans le mélange liquide-vapeur. Pour l’unité de masse de corps, x est la masse de vapeur et 1 - x la masse de liquide. Soit |
La pression de vapeur saturante étant une fonction de T, les variables d’état indépendantes pour le mélange liquide-vapeur sont x et T.
1. Etude énergétique des vapeurs saturantes
La quantité de chaleur Q échangée pour passer
de A1 à A suivant le palier de liquéfaction
est :
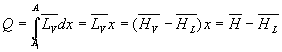
L’énergie interne en A sera : ![]()
L’entropie en A sera : 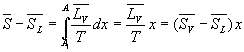
On remarquera l’analogie des formules donnant le titre en fonction des
volumes, des enthalpies, des énergies internes et des entropies.
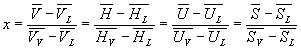
Capacités calorifiques massiques de vapeur saturante et de liquide saturant
Soit dQ’ la quantité de chaleur
échangée dans la transformation allant de A2
à A’2 suivant la courbe de rosée.
![]() est la capacité
calorifique massique de la vapeur saturante.
est la capacité
calorifique massique de la vapeur saturante.
De même, suivant la courbe d’ébullition, on définit la capacité
calorifique massique du liquide saturant ![]() .
.
La capacité calorifique du liquide saturant est très
proche (sauf au voisinage du point critique) de la capacité calorifique
du liquide à volume constant.
La capacité calorifique de la vapeur saturante est inférieure
et très différente de celle de la capacité calorifique
à volume constant de la vapeur sèche. Elle est assez souvent
négative, ce qui veut dire que, pour diminuer la température
d’une vapeur saturante, il faut lui fournir de la chaleur.
Pour l’unité de masse de corps, nous considérons la transformation
de l’état A(x, T) à l’état A’’(x+dx, T+dT)
en utilisant l’état intermédiaire A’(x, T+dT).
La quantité de chaleur échangée pour passer de
l’état A à l’état A’’ est :
![]()
La variation d’entropie entre A et A’’ sera : ![]()
La variation d’enthalpie entre A et A’’ sera :
![]()
En écrivant la relation de Cauchy sur les deux formes différentielles
qui sont des différentielles totales exactes et en tenant compte de la
relation ![]() ,
on obtient sans difficulté particulière les très importantes
relations de Clapeyron.
,
on obtient sans difficulté particulière les très importantes
relations de Clapeyron.
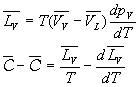 |
Nous nous sommes appuyées sur l’équilibre liquide-vapeur. Pour les équilibres liquide-solide et solide-gaz, nous pouvons faire des raisonnements analogues (en particulier pour les relations de Clapeyron). |
Il existe plusieurs démonstrations des relations de Clapeyron, celle (non présentée) faisant intervenir la fonction d’état enthalpie libre et la notion de potentiel chimique nous parait la plus intéressante.
" Justification " des formules de Dupré et Rankine
Loin du point critique, ![]() est très inférieur à
est très inférieur à ![]() (pour l’eau
(pour l’eau ![]() et
et ![]() à
100 °C ; la température critique est 374,2 °C)
à
100 °C ; la température critique est 374,2 °C)
![]() si on admet
que la vapeur sèche jusqu’à sa limite saturante obéit à
l’équation d’état des gaz parfaits.
si on admet
que la vapeur sèche jusqu’à sa limite saturante obéit à
l’équation d’état des gaz parfaits.
![]() la formule
de Dupré si
la formule
de Dupré si ![]() pour l’intervalle de température ou la formule de Rankine si
pour l’intervalle de température ou la formule de Rankine si ![]() .
.