Exercices de base en Thermodynamique

Exercices sur les transferts et bilans énergétiques

1 - Un gaz parfait est contenu dans un cylindre fermé par un piston. On suppose que les parois du cylindre et du piston sont infiniment perméables à la chaleur de manière que les transformations étudiées soient isothermes. Les conditions initiales sont ,,.
1) On comprime le gaz de manière réversible de à . Calculer le travail échangé au cours de l’opération. Quel est le travail échangé par le gaz lorsqu’il se détend de manière réversible de à . Comparer et (signe et valeur).
2) On comprime le gaz de manière irréversible de à en appliquant brutalement sur la face extérieure du piston la pression . Calculer le travail échangé au cours de cette opération. Quel est le travail échangé par le gaz lorsqu’il se détend de à , en laissant agir la pression sur la face extérieure du piston. Comparer et . Comparer et . On prendra = 1 atm et = 10 atm .

| Méthodologie | Réponse 1 | Réponse 2

2 – L’énergie interne U d’un gaz parfait s’obtient à partir de la relation . On considère le cas .
1) Calculer U.
2) Calculer la différentielle dS de l’entropie S du gaz parfait que l’on exprimera successivement avec le couple de variables (T, V), (T, p) puis (p, V). Exprimer la fonction entropie S avec les trois couples de variables.
3) Comment sont affectés les résultats des questions 1) et 2) si dépend de la température.
4)a) Montrer que dans le cas d’une transformation réversible isotherme à la température de la pression à la pression , on peut calculer les quantités de travail et de chaleur échangées par le gaz parfait par deux méthodes différentes.
4)b) Comment pourrait-on calculer l’entropie créée dans le cas d’une transformation isotherme irréversible à température , la pression étant appliquée brutalement sur la face extérieure du piston.

3 - Une masse d’air (assimilé à un gaz parfait) occupe un volume la pression atmosphérique et à la température . On la comprime par une opération réversible jusqu’à une pression .
1) En supposant que, pendant cette compression, la température du gaz soit maintenue constante, calculer le travail échangé pour effectuer la compression. Calculer la variation d’énergie interne et la quantité de chaleur échangée pendant cette compression.
2) En supposant que la compression soit faite de manière adiabatique, calculer le volume final et la température finale de l’air. Calculer le travail échangé, montrer qu’il s’exprime en fonction des températures finale et initiale. Retrouver ce résultat par la considération de l’énergie interne.
3) On comprime adiabatiquement le gaz, en partant du même état initial, jusqu’à une pression p’ , puis on le laisse refroidir sans changer son volume jusqu’à la température ambiante . On veut, après refroidissement, obtenir de l’air à la pression .
Calculer la pression p’ , le travail échangé au cours de la compression adiabatique, ainsi que la chaleur échangée pendant le refroidissement.
A.N.

4 - On considère une mole de gaz parfait diatomique initialement dans l’état 0 (; ; ).
On amène ce gaz dans l’état 1 (; ; ) de deux manières différentes :
a / par compression adiabatique réversible,
b / par compression isotherme réversible jusqu’à la pression puis échauffement à pression constante jusqu’à la température .

1) Représenter les évolutions a / et b / sur un diagramme (p en ordonnées, V en abscisse)
2) Calculer les travaux et les quantités de chaleur au cours de chacune des évolutions. Conclusions.

5 - On dispose dans un cylindre fermé par un piston une certaine masse d’un gaz parfait diatomique (). Les parois du cylindre et du piston sont isolées et supposées imperméables à la chaleur. Dans les conditions initiales, le volume occupé par le gaz est , la pression est et la température .
1) Calculer la capacité calorifique relative à cette masse de gaz.
2) On comprime ce gaz de manière réversible jusqu’à .
2)1) Dans quelle(s) condition(s) la réversibilité est-elle réalisée ?
2)2) Calculer .
2)3) Calculer le travail au cours de l’évolution.
3) On comprime maintenant le gaz en partant du même état initial () mais en appliquant brutalement .
3)1) Que peut-on dire de la transformation ?
3)2) Exprimer le travail échangé par le système de deux manières différentes.
3)3) En déduire la valeur de en fin d’évolution ainsi que . Comparer ces résultats à ceux de la question 2). Expliquer la différence.
4) On retire l’isolant thermique qui entourait le cylindre, les parois deviennent perméables à la chaleur. On réalise un refroidissement isobare de l’état () à l’état ().
Calculer la quantité de chaleur échangée au cours de cette transformation.

6 - Un cylindre indéformable dont les parois sont adiabatiques contient de l’azote (assimilé à un gaz parfait) réparti dans deux compartiments A et B séparés par un piston également adiabatique. Ce piston peut se mouvoir sans frottement. Le compartiment A contient de gaz, le compartiment B contient de gaz.
Dans A, une résistance électrique de capacité calorifique négligeable permet de chauffer le gaz. La transformation subie par le gaz du compartiment B est considérée comme réversible.
1) Initialement, la température et la pression sont les mêmes dans les deux compartiments. Calculer le volume V du cylindre.
2) A reçoit une quantité de chaleur Q. Ecrire les variations d’énergie interne du système complet en appelant la température finale dans A et la température finale dans B. En déduire la pression finale p.
3) Que peut-on dire de l’évolution subie par le gaz dans le compartiment B ?
En déduire puis .
A.N. ; ; ;

7 - On désire refroidir une mole de gaz parfait diatomique en lui faisant subir une suite de compressions isothermes suivies de détentes adiabatiques. Ce gaz est contenu dans un cylindre fermé par un piston glissant sans frottement. Initialement, le gaz est à la température et sa pression est .
Justifier la valeur de .
1) Dans une première opération on comprime le gaz de manière isotherme réversible jusqu’à la pression puis on le détend de manière adiabatique réversible jusqu’à .
1)1) Quelle est la température en fin d’évolution adiabatique ?
1)2) Calculer la quantité de chaleur et le travail mis en jeu au cours de l’évolution isotherme, ainsi que le travail mis en jeu au cours de l’évolution adiabatique. En déduire le travail total W reçu par le gaz au cours de cette première opération.
Calculer la variation d’entropie au cours de cette première opération.
2) Le gaz étant dans l’état on recommence la même opération (compression isotherme réversible jusqu’à , puis détente adiabatique réversible jusqu’à ).
2)1) Donner l’expression de la température obtenue à la fin de la n^ième opération.
2)2) Pour quelle valeur de n le gaz atteint-il une température inférieure ou égale à 100K?
2)3) Calculer la variation d’entropie après n opérations.
3) On suppose maintenant qu’au cours de chaque opération, la compression isotherme et la détente adiabatique sont irréversibles (pour cela, on soumet le piston à la pression extérieure tout au long de l’évolution isotherme puis on le lâche de façon qu’au cours de la détente adiabatique de à la pression appliquée soit constamment la pression atmosphérique ).
Calculer le travail et la chaleur mis en jeu au cours de la première compression isotherme. Comparer à et trouvés en 1)b), expliquer la différence.
Calculer la température obtenue à la fin de la première détente adiabatique ainsi que le travail échangé par le gaz au cours de cette détente. Comparer ces résultats à ceux obtenus quand la détente adiabatique était réversible. Conclusions ?
Calculer la variation d’entropie après la première compression isotherme et la première détente adiabatique. Calculer les entropies créées dans la compression isotherme et dans la détente adiabatique.

8 - Un cylindre de section fermé par un piston P₁ de masse négligeable est divisé en deux compartiments A et B au moyen d’une paroi mobile P₂ de masse négligeable pouvant se déplacer librement.
Les parois du cylindre et du piston P₁ sont adiabatiques alors que la paroi P₂ initialement adiabatique peut être rendue conductrice de la chaleur au moyen d’un dispositif approprié.
Dans l’état initial le compartiment A contient 2 moles d’hélium (gaz monoatomique), le compartiment B contient 1 mole d’oxygène ( diatomique ).

Les deux gaz que l’on supposera parfaits sont à la même température et le système est en équilibre sous l’action d’une force extérieure s’exerçant sur P₁ .
1) Calculer les volumes et occupés par chaque gaz.
2) On modifie lentement la force extérieure jusqu’à la valeur . Calculer les volumes et occupés par chaque gaz ainsi que la température et . Quel est le travail W échangé. Quels sont les travaux et échangés par chaque gaz.
3) Le système étant dans l’état initial (,) on rend la paroi P₂ conductrice et on réalise à nouveau une compression infiniment lente de à .
Que peut-on dire des transformations subies par chaque gaz et par le système complet ?
Quelle relation lie les paramètres température et pression p au cours de l’évolution ?
Calculer la température d’équilibre finale ainsi que les travaux , et W’ échangés par chaque gaz et par le système dans son ensemble. Comparer ces résultats à ceux en 2).
4) Le système étant dans l’état initial (,) on pratique une ouverture dans la paroi P₂ , les deux gaz se mélangent, la paroi P₂ est déposée au fond du cylindre et ne joue plus aucun rôle. On réalise alors la compression infiniment lente de à .
Que peut-on dire des deux phases successives de l’évolution ?
Que peut-on dire de la température d’équilibre finale et du travail échangé par le système ?

9 - Un réservoir indéformable de volume dont les parois sont adiabatiques est muni d’un robinet R permettant de le mettre en communication avec l’air atmosphérique extérieur.
On assimilera ce dernier à un gaz parfait diatomique de masse molaire , de . Justifier ces valeurs.
1) Le réservoir étant rempli d’air à la température dont la pression est .
Calculer la masse d’air qu’il contient.
2) On ouvre brusquement le robinet R de manière à ramener la pression de l’air dans le réservoir à la valeur de la pression atmosphérique .

Expliquer pourquoi on peut considérer que l’air restant dans le réservoir s’est détendu de manière adiabatique quasi-statique. Calculer la température et la masse de l’air restant dans le réservoir à la fin de cette détente.
3) On suppose maintenant que l’on a fait le vide dans le réservoir. On ouvre brusquement le robinet R, l’air pénètre dans le réservoir jusqu’à ce que la pression soit égale à la pression extérieure .
3)1) Expliquer la nature de cette opération et donner une expression littérale du travail W échangé au cours de l’opération (pour cela, on considérera un système constitué de la quantité d’air entrant dans le réservoir).
3)2) Calculer la température de l’air ainsi que le travail W.
4) Le robinet R étant fermé on établit le contact thermique entre l’intérieur et l’extérieur du réservoir en enlevant l’isolant qui protégeait les parois. La température de l’air passe alors de à . Calculer la chaleur et le travail échangés.

10 – Un cylindre horizontal est fermé à l’une de ses extrémités par une paroi fixe F₀ et à l’autre l'extrémité par un piston qui peut coulisser sans frottement le long du cylindre.
Le cylindre est séparé en deux compartiments A et B par une paroi fixe F.
Sur la face extérieure du piston s’exerce la pression atmosphérique qu’on suppose uniforme et constante.
1) Dans la situation initiale le compartiment A de volume contient un gaz parfait diatomique à température , le compartiment B de volume est vide.
Calculer le nombre n de moles dans le cylindre.

2) Les parois du cylindre et le piston sont imperméables à la chaleur et de capacités calorifiques négligeables.
On perce un orifice dans la paroi fixe F.

Le volume est suffisamment grand pour que la pression finale soit inférieure à .
2)1) En déduire, dans l’état final, le volume du compartiment A.
2)2) Calculer par deux méthodes différentes le travail échangé avec l’extérieur par le gaz. En déduire la température finale, la pression finaledu gaz et le volume minimal pour que la pression finale reste inférieure à .
2)3) Calculer l’entropie créée. Le résultat est-il conforme au second principe de la Thermodynamique ?

3) On revient aux conditions définies en 1), les parois du cylindre et le piston étant imperméables à la chaleur et de capacités calorifiques négligeables.
est maintenant inférieur à et la pression finale du gaz sera après avoir percé l’orifice.
3)1) Calculer par deux méthodes différentes le travail échangé avec l’extérieur par le gaz. En déduire la température finale.
3)2) Calculer l’entropie créée. Le résultat est-il conforme au second principe de la Thermodynamique ?
4) On revient aux conditions initiales et on bloque le piston. Que se passe t’il lorsque l’on perce l’orifice ? Conclusions.

11 - Expérience de Clément et Desormes

Soit un ballon de volume V muni de deux tubulures, l’une terminée par un robinet, l’autre raccordée à un manomètre rempli d’un liquide de masse volumique m . On néglige le volume des tubulures.

A l’instant initial le ballon est rempli d’un gaz parfait à la température ambiante et la dénivellation du liquide dans le manomètre est h comme indiqué sur le schéma.
1) On suppose que la différence de pression entre le ballon et le milieu extérieur est petite comparée à la pression extérieure . On ouvre le robinet le temps juste nécessaire pour établir l’équilibre des pressions entre le ballon et l’extérieur et on referme le robinet.
Calculer la variation de température du gaz au cours de cette détente.

On laisse ensuite le système échangé de la chaleur avec le milieu extérieur de telle sorte que les températures dans le ballon et à l’extérieur deviennent égales.
2) Donner l’expression de la nouvelle dénivellation h’ du liquide. En déduire l’expression de g en fonction de h et h’.
A.N. ; ;

| Méthodologie | Réponse 1 | Réponse 2 |

12 - On considère un récipient fermé par un piston de masse mobile sans frottements dans le col vertical de section d’un récipient.

Le récipient contient n moles de gaz parfait dont on cherche à déterminer le rapport .
A l’extérieur, l’air est à pression .
A l’équilibre, le volume intérieur du récipient est .
1) Calculer la pression du gaz intérieur à l’équilibre.
2) Le piston est déplacé de sa position d’équilibre et lâché sans vitesse initiale. Les transformations ultérieures sont quasi-statiques mais assez rapides pour être adiabatiques.
2)1) Décrire la nature des mouvements (de faible amplitude) du piston.

2)2) Soit z la position du piston par rapport à sa position d’équilibre. Ecrire la variation de volume du gaz intérieur.
2)3) Trouver une relation entre les variations de volume et du gaz intérieur (ces variations restent faibles devant respectivement V et ).
2)4) En déduire l’équation différentielle du mouvement du piston. Donner l’expression théorique de la période du mouvement. Si est la période, calculer g .
2)5) Que deviendraient ces résultats pour des gaz réels ?

13 - Un cylindre (C), indéformable d’axe horizontal Ox, de section s, a des parois parfaitement calorifugées. Il est séparé en deux compartiments par un piston (P), parfaitement calorifugé, de masse m, mobile sans frottement. Les compartiments 1 et 2 contiennent chacun une mole de gaz parfait, initialement dans l’état ( ). On prendra constant.

Un opérateur extérieur déplace légèrement le piston et l’abandonne sans vitesse initiale.
1) Expliquer pourquoi les transformations peuvent être prises réversibles.
2) Calculer, en première approximation, les pressions (respectivement de chaque compartiment) en fonction de la position du piston à l’instant considéré.
3) Ecrire pour le piston (P) de masse m le principe fondamental de la dynamique et en déduire la période des oscillations du piston.

On rappelle que

14 - Deux systèmes notés 1 et 2, initialement à température et , de capacités calorifiques à pression constante et sont mis en contact thermique, la pression restant constante au cours de l’évolution. Au bout d’un temps suffisamment long, il s’établit un état d’équilibre où les deux systèmes ont même température (principe 0).
1) La transformation est-elle réversible ?
2) Calculer les quantités de chaleur et échangées par chacun des systèmes ainsi que la température finale .
3) Calculer les variations d’entropie , de chacun des deux systèmes et de l’ensemble des deux systèmes.
4)1) On se place dans le cas , quels sont les signes de , et ?
4)2) On se place dans le cas , quels sont les signes de , et ?
4)3) Onfera l'étude mathématique de dans le cas
5) on étudie le cas où le système 2 a une capacité calorifique " infinie " (atmosphère, eau d’un lac, ...).
Que deviennent les résultats des questions précédentes ? On étudiera mathématiquement en fonction de .
6) Reprendre le texte, les raisonnements et les résultats si les transformations pour chacun des systèmes sont isochores.

15 - On considère un cylindre métallique conducteur de l’électricité, de section et de longueur . Sa capacité calorifique est , sa masse volumique est , sa résistance électrique est, sa température initiale est . Les transformations ont lieu à pression constante et on supposera que le matériau constituant le cylindre est suffisamment bon conducteur de la chaleur pour que sa température puisse être considérée comme uniforme.
1) On applique aux bornes de ce conducteur une tension pendant un temps , tout en le maintenant à la température dans un bain isotherme de même température.
1)1) Que peut-on dire de cette opération ?
1)2) Quelle est la nature de l’énergie électrique ? Quelle est la chaleur échangée par le conducteur ?
1)3) Calculer, pour le conducteur, la variation d’entropie, l’entropie échangée, l’entropie créée au cours de cette opération.
2) On applique aux bornes de ce conducteur une tension pendant un temps , en l’entourant d’une gaine parfaitement imperméable à la chaleur.
2)1) Quelle est la température finale du conducteur ?
2)2) Calculer, pour le conducteur, la variation d’entropie, l’entropie échangée, l’entropie créée au cours de cette deuxième opération.

16 - On se propose d'étudier un fusible constitué d'un fil de plomb de longueur l, de rayon r, parcouru par un courant électrique d'intensité I. La température de fusion du plomb est égale à .
On rappelle l'expression de la puissance électrique dissipée par effet Joule où est la résistivité électrique du plomb.

1) Le fusible échange dans de l'air environnant à température
Quels modes de transfert de chaleur interviennent dans ces échanges (on donnera une explication qualitative pour chacun des modes).

2) On rappelle les expressions des densités de flux de chaleur d'échanges par convection et par rayonnement thermique et avec .
2)a) Comment appelle t'on la constante ?
2)b)
Montrer qu'aux températures ordinaires (), les échanges par convection sont du même ordre de grandeur que ceux par rayonnement.
On utilisera l'identité
2)c) Comparer à la température de fusion du plomb, les échanges par convection et ceux par rayonnement.
Calculer la densité de flux de chaleur totale échangée.

3) On désire établir, à la température de fusion du plomb c'est à dire à la température de "claquage" du fusible, la relation entre l'intensité I et le rayon r du fusible.
3)a) A partir d'un bilan thermique où on considère que tout le fusible est à température , établir la relation liant P, et la surface latérale du fusible.
3)b) En déduire la relation liant I et r. Représenter la courbe . Quelle intensité supporte un fusible de rayon ?

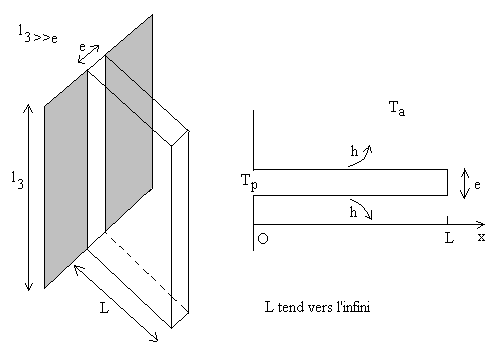
17 - Ailette à section constante semi-infinie

On considère une paroi à température au contact d’un fluide à température .

1) Exprimer la densité de flux de chaleur entre la paroi et le fluide

2) On place sur une partie de cette paroi un ailette de section constante (figure ci-après).
2)1) Etablir, à partir d’un bilan énergétique, l’équation différentielle qui régit le champ de température permanent [on considérera qu’en chaque section le champ de température peut, en première approximation, être pris uniforme].
2)2) Ecrire les équations aux limites en et .
2)3) Déterminer le champ de température ; en déduire le flux de chaleur échangé entre l’ailette et le fluide.

3) En déduire l’efficacité rapport du flux de chaleur échangé par l ‘ailette au flux échangé par la paroi sans ailette pour une même section.
Que deviennent les résultats précédents pour une ailette semi-infinie de section constante à symétrie de révolution de rayon R.

18 - On linéarise les lois d’échanges de la chaleur par convection et rayonnement thermique si bien que les densités de flux de chaleur, respectivement et , sont égales à :

où et sont les coefficients d’échanges respectivement de convection et de rayonnement, où est la température de paroi du corps échangeant,
les températures de référence du milieu environnant.
Dans tout le problème, on posera .

1) L’étude des phénomènes de convection et de rayonnement thermique conduit, en fait, aux lois suivantes :

où est la constante de Stéfan-Boltzmann et le facteur de forme que nous prendrons dans tout le problème égal à 1.
Etablir un tableau, pour des valeurs de égales à , avec les valeurs de ,, ,, et .
Comparer les valeurs de et . Conclusion.

2) Un matériel électronique dissipant une puissance P est enfermé dans une boite métallique en forme de parallélépipède rectangle de coté , et .
2)a) Expliquer pourquoi on peut considérer que les parois de la boite sont à température uniforme notée .
2)b) Chacune des faces de la boite échangeant par convection et rayonnement conformément à la question 1), compléter le tableau par les valeurs de P correspondant aux différentes valeurs de .

3) La puissance dissipée étant , la température de paroi ne pouvant dépasser 343 K, on place des ailettes sur l’une des faces de dimensions ,.
3)a) Expliquer pourquoi la présence d’ailettes diminue la température de paroi.
3)b) Pour et , calculer le flux de chaleur que doit évacuer la face avec ailettes (en fait on calculera le flux de chaleur évacué par les faces sans ailettes et on déduira celui que doit évacuer la face avec ailettes; on pourra utiliser les résultats du tableau ou un coefficient ).
Comparer ce flux à celui que la face évacue sans ailettes.
3)c) Les ailettes de section rectangulaire (épaisseur e, hauteur ) sont supposées semi-infinies, la conductivité du matériau les constituant est .
L’efficacité d’une ailette rectangulaire semi-infinie est égale à .
Calculer .
En déduire le nombre N d’ailettes nécessaires.