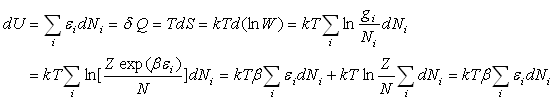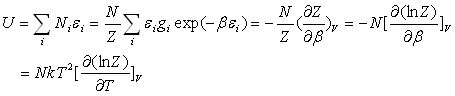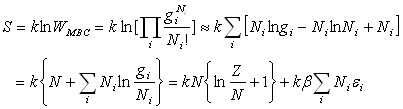Physique statistique
Plan
1. Répartition microscopique des particules et
état macroscopique d'équilibre
2. Répartition statistique de Bose - Einstein
3. Répartition statistique de Fermi - Dirac
4. Relation de Boltzmann entre l'entropie et le nombre
de complexions
5. Limite commune des statistiques de Bose - Einstein
et Fermi - Dirac : statistique corrigée de Maxwell - Boltzmann
En Physique quantique, on apprend que l’énergie d’une particule
est quantifiée, c’est à dire que les valeurs possibles pour
l’énergie forment un spectre discret. Même si, dans un certain
nombre de situations courantes, pour une particule et encore plus pour
un système constitué d’un grand nombre de particules, les
niveaux d’énergie sont si serrés que l’on peut traiter, sur
le plan mathématique, ce spectre comme continu, il n’empêche
qu’en toute rigueur ils sont quantifiés.
Une particule, ayant un niveau d’énergie 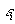 ,
peut être dans différents sous-états.
,
peut être dans différents sous-états.
Nous savons (nous n’avons pas utilisé l’équation de Schrödinger
pour le montrer strictement) que, pour décrire un atome, on introduit
quatre nombres quantiques, à savoir :
- le nombre quantique principal qui quantifie l’énergie,
- le nombre quantique secondaire qui quantifie le moment cinétique,
-le nombre quantique magnétique qui quantifie le moment
magnétique,
- le spin qui quantifie la rotation propre des électrons
de l’atome.
Ainsi pour une même énergie (pour une valeur particulière
du nombre quantique principal), un atome peut posséder différentes
valeurs des nombres quantiques secondaire, magnétique ou de spin.
Pour qualifier la possibilité de sous-états correspondant à
une même énergie, on emploie l’expression dégénérescence
(ou poids statistique) et on traduit par la variable 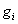 le nombre de dégénérescences correspondant à un
même niveau d’énergie
le nombre de dégénérescences correspondant à un
même niveau d’énergie 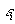 .
.
1. Répartition microscopique
des particules et état macroscopique d’équilibre.
On considère un grand nombre N de particules, de même nature,
à l’équilibre, d’énergie interne U fixée
; les niveaux d’énergie possibles 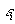 pour chaque particule étant eux aussi fixés. Par suite,
pour chaque particule étant eux aussi fixés. Par suite, 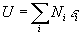 où
où 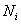 est le nombre de particules (parmi les N) occupant le niveau d’énergie
est le nombre de particules (parmi les N) occupant le niveau d’énergie
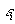 .
.
La quantité 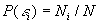 représente la probabilité pour une particule d’occuper le niveau
d’énergie
représente la probabilité pour une particule d’occuper le niveau
d’énergie 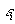
Compte tenu de la dégénérescence et du grand nombre de
particules, il existe un grand nombre de sous-états (chaque sous-état
est appelé complexion) correspondant à la même répartition 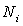 sur les niveaux d’énergie
sur les niveaux d’énergie 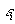 .
.
On note W le nombre de complexions et la répartition la
plus probable est celle qui correspond à un maximum du nombre de complexions.
Quiconque a étudié un tant soit peu le calcul des probabilités
en Mathématiques sait que ce maximum est très aigu si le nombre
d’éléments est grand.
Le maximum du nombre de complexions correspond à un état de répartition
si énormément plus probable que les autres que cette répartition
est d’une part pratiquement sur et d’autre part, lorsqu’elle est réalisée,
stable : elle correspond à l’état d’équilibre macroscopique
qui n’est déplaçable que par une action extérieure et vers
lequel a évolué tout système.
Nos propos traduisent un lien, une corrélation entre le nombre
de complexions et l’entropie qui, rappelons le, est maximale pour un système
isolé en équilibre.
Les différents types de particules
Sans entrer dans des explications qui feraient intervenir la parité
ou non des fonctions d’onde, il existe deux types de particules :
- celles ayant un spin nul ou entier (photon, phonon,  ,
Méson
,
Méson 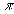 )
qui obéissent à la statistique de Bose-Einstein : ces particules
sont appelées des bosons, elles peuvent occuper plusieurs sous-états
identiques,
)
qui obéissent à la statistique de Bose-Einstein : ces particules
sont appelées des bosons, elles peuvent occuper plusieurs sous-états
identiques,
- celles ayant un spin demi-entier (électron, proton, neutron, neutrino,
méson 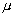 )
qui obéissent à la statistique de Fermi-Dirac : ces particules
sont appelées des fermions, il ne peut y avoir plus d’un fermion
par sous-état (principe d’exclusion de Pauli)
)
qui obéissent à la statistique de Fermi-Dirac : ces particules
sont appelées des fermions, il ne peut y avoir plus d’un fermion
par sous-état (principe d’exclusion de Pauli)
2. Répartition statistique de
Bose-Einstein
Le niveau d’énergie 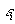 est divisé en
est divisé en 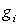 sous-états où " se répartissent ", sans règle,
sous-états où " se répartissent ", sans règle, 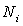 particules.
particules.
Nous disposons de 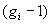 sous-états indépendants et de
sous-états indépendants et de 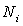 particules interchangeables.
particules interchangeables.
Nous pouvons faire 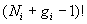 permutations qui ne correspondent pas toutes à des sous-états
différents. En effet, nous pouvons interchanger les sous-états
sans qu’il y ait de différence entre les sous-états.
permutations qui ne correspondent pas toutes à des sous-états
différents. En effet, nous pouvons interchanger les sous-états
sans qu’il y ait de différence entre les sous-états.
Au niveau microscopique, pour vérifier les résultats expérimentaux,
nous devons faire l’hypothèse de l’indiscernabilité des particules
(cette hypothèse n’est pas évidente puisqu’au niveau macroscopique
deux objets identiques sont reconnaissables c’est à dire discernables).
Ceci revient à diviser le nombre de permutations respectivement par 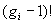 et par
et par  ; on
obtient le nombre de combinaisons
; on
obtient le nombre de combinaisons 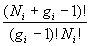 .
.
Il en sera, de même pour les autres niveaux d’énergie et nous devons
combiner tout sous-état d’un niveau d’énergie avec tous les autres
sous-états des autres états d’énergie.
Par suite,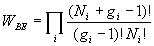
Nous cherchons le maximum de 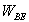 (en fait de
(en fait de 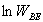 ,
la fonction logarithme étant monotone) en utilisant la relation de Stirling
,
la fonction logarithme étant monotone) en utilisant la relation de Stirling  si x grand (ð
si x grand (ð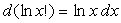 ).
).
Les 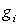 étant fixés, il vient
étant fixés, il vient 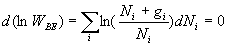 auquel nous devons associer
auquel nous devons associer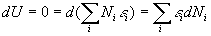 et
et 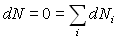 [cette dernière relation ne peut être appliquée pour les
photons qui ne sont pas en nombre constant puisqu’ils peuvent être absorbés
ou créés et émis].
[cette dernière relation ne peut être appliquée pour les
photons qui ne sont pas en nombre constant puisqu’ils peuvent être absorbés
ou créés et émis].
Nous appliquons la méthode des multiplicateurs de Lagrange :
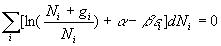 ð
ð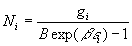 en posant
en posant 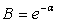
Le facteur B se calcule à partir de 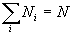 , le facteur
, le facteur 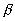 sera identifié à
sera identifié à 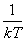 .
.
Pour les photons, on ne peut utiliser la relation 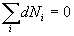 et la méthode des multiplicateurs de Lagrange se limite à
et la méthode des multiplicateurs de Lagrange se limite à 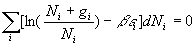 ð
ð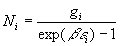
3. Répartition statistique de
Fermi-Dirac
Il ne peut y avoir qu’une particule par sous-état ð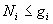 .
.
Il y a donc 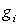 sous-états occupés et
sous-états occupés et 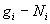 sous-états non occupés.
sous-états non occupés.
Par suite, 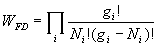 .
.
On obtient 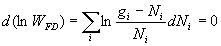 et
et 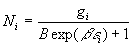 à
l’aide de la méthode des multiplicateurs de Lagrange.
à
l’aide de la méthode des multiplicateurs de Lagrange.
4. Relation de Boltzmann entre l’entropie
et le nombre de complexions
Le nombre de complexions correspondant à l’addition de deux systèmes
est donné par 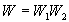 (ð
(ð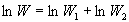 ).
).
L’entropie correspondant à l’addition de deux systèmes est donnée
par 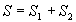 .
.
Nous avons déjà noté la nécessité d’un lien
entre nombre de complexions et entropie. Ce lien est connu sous le nom de relation
de Boltzmann : 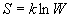 .
.
5. Limite commune des statistiques
de Bose-Einstein et de Fermi-Dirac : statistique corrigée de Maxwell
- Boltzmann
5.1. Limite commune
Les deux statistiques ont une limite commune 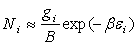 si
si 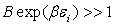 .
.
Cette condition correspond à des conditions physiques souvent réalisées.
Cette limite commune porte le nom de répartition statistique corrigée
de Maxwell-Boltzmann.
Remarque 1 : Le nombre de complexions de cette limite
correspond à 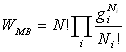
Les 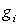 étant fixés, il vient
étant fixés, il vient 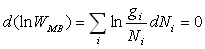 auquel nous devons associer
auquel nous devons associer 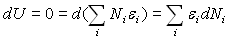 et
et

La méthode des multiplicateurs de Lagrange permet d'écrire :
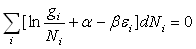 ð
ð
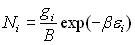 en posant
en posant 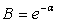
Remarque 2 : 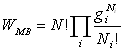 est le nombre de complexions si on considère les particules discernables alors
que
est le nombre de complexions si on considère les particules discernables alors
que 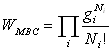 correspond
au nombre de complexions si on considère les particules indiscernables.
correspond
au nombre de complexions si on considère les particules indiscernables.
En effet, soient des niveaux d'énergie 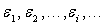 de dégénérescence
de dégénérescence 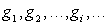 ,
N particules sur ces différents niveaux d'énergie c'est à dire
,
N particules sur ces différents niveaux d'énergie c'est à dire 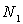 sur le niveau 1, …,
sur le niveau 1, …, 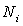 sur le niveau i, …
sur le niveau i, …
Il existe, pour le niveau d'énergie i, 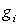 sous-états possibles, donc
sous-états possibles, donc 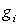 façons de placer une particule sur le niveau d'énergie i,
façons de placer une particule sur le niveau d'énergie i, 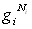 donc de placer les
donc de placer les 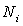 particules du niveau i soit
particules du niveau i soit 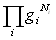 pour
les N particules réparties sur l'ensemble des sous-états.
pour
les N particules réparties sur l'ensemble des sous-états.
Si nous permutons deux particules à l'intérieur d'un même niveau d'énergie,
nous obtenons la même énergie totale. Ainsi, le nombre de répartitions doit
être divisé par 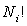 et au total on obtient
et au total on obtient 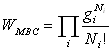 .
.
Si nous considérons que les N particules sont discernables, toute permutation
entre deux particules est une nouvelle complexion. Nous avons 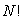 façons de permuter N particules et le nombre de complexions devient,
avec l'hypothèse de discernabilité des particules,
façons de permuter N particules et le nombre de complexions devient,
avec l'hypothèse de discernabilité des particules, 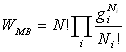 .
.
On montre que l'hypothèse de discernabilité des particules n'est pas en accord
avec la propriété d'additivité de l'entropie : il convient donc d'utiliser
la statistique corrigée de Maxwell-Boltzmann.
Remarque 3 : la limite commune des deux statistiques
revient à la condition 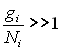
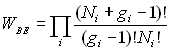 ð
ð 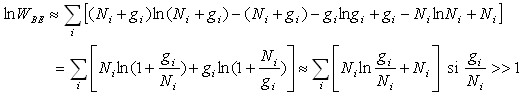
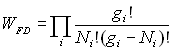 ð
ð 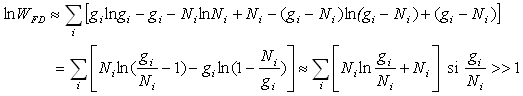
Soit 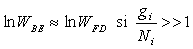
Remarque 4 : la répartition statistique corrigée
de Maxwell-Boltzmann est une excellente approximation si les effets quantiques
ne se font pas sentir c'est à dire si la distance moyenne entre particules
est très supérieure à la longueur d'onde de De Broglie
associée au mouvement des particules.
5.2. La fonction de partition Z
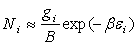
Le calcul de B se fait à partir de 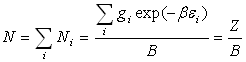 ð
ð  où
où 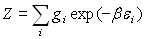 est
appelée la fonction de partition.
est
appelée la fonction de partition.
5.3. Relation entre le paramètre b
et la température
L'énergie interne du système est égale
à : 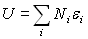 ð
ð
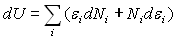
Le calcul quantique des 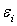 montre qu'ils sont constants si le volume du système est constant.
montre qu'ils sont constants si le volume du système est constant.
On peut donc écrire,
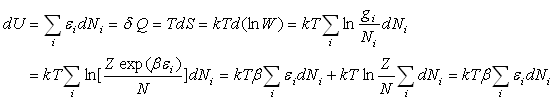
Par identification, 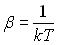
5.4. Importance de la fonction de partition 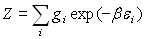
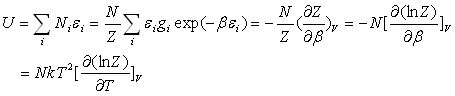
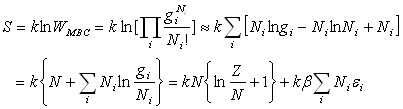
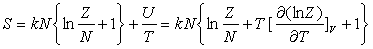
Remarque : dans le cadre de la statistique (non corrigée)
de Maxwell-Boltzmann,

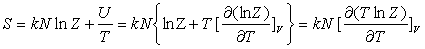
Cette dernière relation ne vérifie pas la propriété d’additivité
de l’entropie.
Les fonctions thermodynamiques sont connues si la fonction
de partition l'est.
Le lecteur étudiera, avec intérêt, l'
animation
de Geneviève Tulloue qui montre comment varie, avec la température,
l'occupation des différents niveaux d'énergie : 
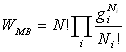
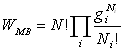 est le nombre de complexions si on considère les particules discernables alors
que
est le nombre de complexions si on considère les particules discernables alors
que 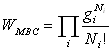 correspond
au nombre de complexions si on considère les particules indiscernables.
correspond
au nombre de complexions si on considère les particules indiscernables.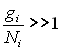
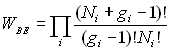 ð
ð 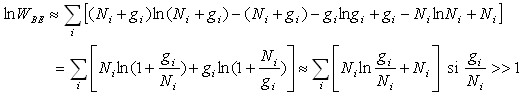
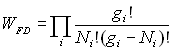 ð
ð 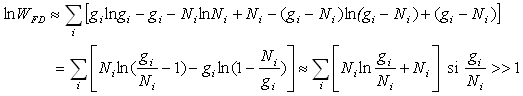
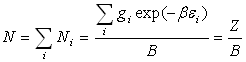 ð
ð