Exercices de physique statistique
1) Complexions, états microscopiques
et états microscopiques
Soient trois niveaux d’énergie (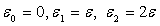 ),
les niveaux 0 et 2 ne sont pas dégénérés, le niveau
1 a une dégénérescence égale à
),
les niveaux 0 et 2 ne sont pas dégénérés, le niveau
1 a une dégénérescence égale à 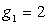 .
.
On considère deux particules notées A et B dont
on veut que l’énergie totale soit égale à  .
.
L’objet de l’exercice est de représenter sur un schéma les différents
états macroscopiques ainsi que les différentes complexions (et/ou
états microscopiques) correspondantes.
1)1) dans le cadre de la statistique de Maxwell-Boltzmann
1)2) dans le cadre de la statistique corrigée de Maxwell-Boltzmann
1)3) dans le cadre de la statistique de Bose-Einstein
1)4) dans
le cadre de la statistique de Fermi-Dirac
| Réponse
11 | Réponse
12 | Réponse
13 | Réponse
14 |
2) Statistique de Maxwell-Boltzmann :
système de particules à deux niveaux d’énergie en équilibre
à température T
Soit un système composé d’un grand nombre de particules N,
chacune possédant deux niveaux d’énergie  (
(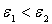 ), de même
poids statistique g. On posera
), de même
poids statistique g. On posera 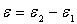 .
.
2)1) Calculer les nombres  de particules d’énergies respectives
de particules d’énergies respectives  .
En déduire les probabilités
.
En déduire les probabilités  pour une particule d’être respectivement sur les niveaux
pour une particule d’être respectivement sur les niveaux  .
.
2)2)a) Calculer 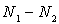 .
.
2)2)b) Définir une température caractéristique 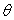 du système.
du système.
2)2)c) Quelles sont les limites de  pour
pour 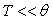 , pour
, pour  .
.
Conclure.
2)3)a) Etablir l’expression de l’énergie interne U du système
(on fera un calcul direct et un calcul utilisant la fonction de partition
Z). Tracer U en fonction de 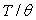 .
.
2)3)b) En déduire et représenter la capacité calorifique
à volume constant 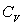 .
.
| Réponse
21 | Réponse
22a | Réponse
22b | Réponse
22c | Réponse
23a | Réponse
23b |
3) Statistique de Maxwell-Botzmann :
étude de la capacité calorifique d’un gaz parfait
3)1) Un état d’énergie e,
pour une particule polyatomique est la combinaison d’un état d’énergie
de translation 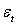 ,
d’un état d’énergie de rotation
,
d’un état d’énergie de rotation  et d’un état d’énergie de vibration
et d’un état d’énergie de vibration 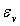 .
.
Ces états sont indépendants, c’est à dire que :
- l’énergie de la particule est la somme des différents termes
d’énergie, soit
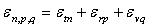 où
où
 sont des entiers,
sont des entiers,
- les particules de même énergie totale
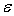 obtenue par des combinaisons différentes des différents termes
d’énergie sont discernables,
obtenue par des combinaisons différentes des différents termes
d’énergie sont discernables,
- la fonction d’onde associée à l’état d’énergie
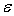
est le produit des fonctions d’onde associées à chacun des termes
constituant cette énergie.
3)1)a) Connaissant les poids statistiques (dégénérescences)
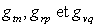 des énergies
des énergies
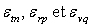 , calculer le poids
statistique de l’état
, calculer le poids
statistique de l’état 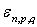 .
.
En déduire la fonction de partition Z connaissant les fonctions
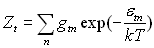 ,
, 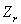 et
et 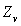 .
.
3)1)b) Montrer que la capacité calorifique à volume constant
se décompose sous la forme 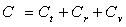 .
.
En déduire que chaque type d’énergie peut être traité
séparément
3)2) Etude de l’énergie de translation
Le mouvement du centre de masse d’une particule possède trois degrés
de liberté, les trois mouvements de translation correspondants sont indépendants
et équivalents.
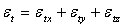 ;
; 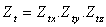 ;
;
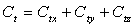
Dans la direction x, les niveaux d’énergie sont donnés
(voir exercice de Mécanique quantique) par :
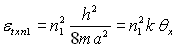 où m
est la masse de la particule, h la constante de Planck, a la dimension
du récipient contenant le gaz dans la direction x,
où m
est la masse de la particule, h la constante de Planck, a la dimension
du récipient contenant le gaz dans la direction x,  un nombre quantique entier positif ou nul, k la constante de Boltzmann
et
un nombre quantique entier positif ou nul, k la constante de Boltzmann
et 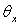 une température
caractéristique du quantum d’énergie de translation dans la direction
considérée.
une température
caractéristique du quantum d’énergie de translation dans la direction
considérée.
Pour les autres directions cartésiennes, on écrira : 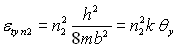 et
et 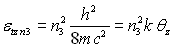
Pour chacune de ces énergies, le poids statistique est égal à
1 (pas de dégénérescence).
3)2)a) Ecrire 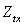 en fonction des températures
en fonction des températures 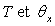 .
.
3)2)b) Calculer 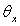 si le gaz est du dioxygène
si le gaz est du dioxygène 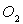 contenu dans un récipient cubique d’un litre.
contenu dans un récipient cubique d’un litre.
3)2)c) Justifier l’hypothèse 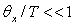 .
En remarquant que la différence d’énergie entre deux états
successifs est infiniment petite, on remplacera la sommation discrète
par une intégrale pour calculer
.
En remarquant que la différence d’énergie entre deux états
successifs est infiniment petite, on remplacera la sommation discrète
par une intégrale pour calculer 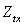 .
.
On rappelle que : 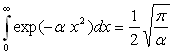
3)2)d) Montrer que 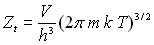 ainsi que la capacité calorifique
ainsi que la capacité calorifique 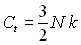 (
(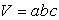 et N
nombre de particules).
et N
nombre de particules).
3)2)e) Calculer l’entropie S suivant la
statistique de Maxwell-Boltzmann et suivant la statistique corrigée de
Maxwell-Boltzmann.
3)3) Etude de l’énergie de rotation
On se limite à des particules diatomiques possédant donc deux
degrés de liberté de rotation.
Les niveaux d’énergie de rotation sont donnés par :
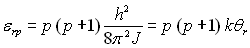 où J
est le moment d’inertie par rapport à toute direction perpendiculaire
nà l’axe joigant les deux atomes et passant par le centre d’inertie 1
et p un nombre quantique entier positif ou nul.
où J
est le moment d’inertie par rapport à toute direction perpendiculaire
nà l’axe joigant les deux atomes et passant par le centre d’inertie 1
et p un nombre quantique entier positif ou nul.
3)3)a) Le poids statistique 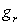 du niveau d’énergie
du niveau d’énergie 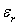 est
est  . Comment
peut-on justifier cette valeur ?
. Comment
peut-on justifier cette valeur ?
3)3)b) Ecrire 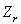 en fonction des températures
en fonction des températures 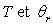 .
.
3)3)c) Calculer 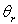 si le gaz est du dioxygène
si le gaz est du dioxygène 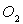 ,
la distance entre les deux atomes est égale à
,
la distance entre les deux atomes est égale à 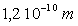 .
.
3)3)d)
Justifier l’hypothèse 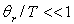 et calculer, compte tenu de cette hypothèse, la capacité calorifique
et calculer, compte tenu de cette hypothèse, la capacité calorifique
 .
.
3)4) Etude de l’énergie de vibration
Dans le cas d’une molécule diatomique, il y a qu’une seule possibilité
de vibration correspondant à la variation de la distance interatomique.
Cette vibration est, en première approximation, de fréquence n
.
Les niveaux d’énergie de vibration sont selon la Mécanique quantique :
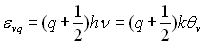 où q
est un nombre quantique entier positif ou nul.
où q
est un nombre quantique entier positif ou nul.
3)4)a) Pour le dioxygène, calculer 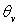 (
(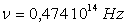 ).
).
3)4)b) Calculer la fonction de partition 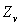 en fonction des températures
en fonction des températures 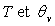 .
.
3)4)c)
Calculer la capacité calorifique 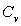 en fonction des températures
en fonction des températures 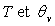 .
Représenter
.
Représenter 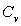 en fonction de
en fonction de  .
.
3)5) Etude de l’énergie totale
3)5)a) Tracer la capacité calorifique 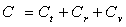 en fonction de
en fonction de  .
.
3)5)b) Que vaut la capacité calorifique C à température
ordinaire ?
3)5)c) Que peut-on déduire sur l’équipartition
de l’énergie ?
| Réponse
31a | Réponse
31b | Réponse
32a | Réponse
32b | Réponse
32c | Réponse
32d | Réponse
32e | Réponse
33a | Réponse
33b | Réponse
33c | Réponse
33d | Réponse
34a | Réponse
34b | Réponse
34c | Réponse
35a | Réponse
35b | Réponse
35c |
4) Statistique de Maxwell-Botzmann :
étude du mélange idéal de deux gaz parfaits diatomiques
Soient  le nombre respectif de particules de deux gaz parfaits
le nombre respectif de particules de deux gaz parfaits  ,
,
 les masses des
particules de chacun des deux gaz. Ces deux gaz ont même température
les masses des
particules de chacun des deux gaz. Ces deux gaz ont même température
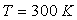 et sont contenus
dans des compartiments de volumes
et sont contenus
dans des compartiments de volumes 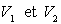 .
.
On effectue, à température constante, le mélange idéal
de ces deux gaz dans un volume 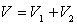 .
.
4)1)a) Que faut-il attendre par l’expression " mélange
idéal " ?
4)1)b) A partir des résultats de l’exercice 3, expliquez
pourquoi l’on peut écrire la fonction de partition de l’un ou l’autre
des gaz sous la forme : 
4)1)c) Calculer l’énergie interne U des deux gaz séparés
et l’énergie interne U’ des deux gaz mélangés. Conclure.
4)1)d) Calculer l’entropie S des deux gaz séparés
et l’entropie S’ des deux gaz mélangés. Conclure à
partir du calcul de  .
.
4)1)e)
Calculer l’énergie libre F’ du mélange. En déduire
la pression p’ du mélange ainsi que la pression partielle 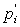 de chacun des deux gaz dans le mélange. En déduire la loi de Dalton.
de chacun des deux gaz dans le mélange. En déduire la loi de Dalton.
| Réponse
41a | Réponse
41b | Réponse
41c | Réponse
41d | Réponse
41e |
4)2) Enthalpie libre et potentiel chimique
4)2)a) Calculer l’enthalpie libre G’ des deux gaz mélangés
en fonction de la température T, de la pression p’ et des
fractions molaires 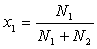 et
et 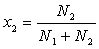 des gaz dans
le mélange.
des gaz dans
le mélange.
4)2)b) En déduire le potentiel chimique 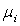 du gaz i dans le mélange rapporté à une particule.
du gaz i dans le mélange rapporté à une particule.
4)2)c) Exprimer l’enthalpie libre G’ en fonction des nombres de
particules  et
des potentiels chimiques
et
des potentiels chimiques 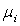 .
.
| Réponse
42a | Réponse
42b | Réponse
42c |
5) Statistique de Bose-Einstein : étude
du rayonnement dans une enceinte (corps noir)
Une enceinte de volume V de température T
est rempli d’ondes électromagnétiques. A toute onde électromagnétique
est associée une corpuscule appelée photon de spin égal
à 1 et obéissant à la statistique de Bose-Einstein.
Le nombre d’états de fréquences comprises entre  est égal à :
est égal à : 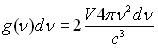 où
où 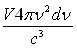 correspond
au calcul habituel du nombre d’ondes de fréquences comprises entre
correspond
au calcul habituel du nombre d’ondes de fréquences comprises entre  et où le facteur 2 est introduit pour tenir compte du fait que toute
onde plane se décompose en deux ondes planes polarisées perpendiculairement.
et où le facteur 2 est introduit pour tenir compte du fait que toute
onde plane se décompose en deux ondes planes polarisées perpendiculairement.
5)1)a) Exprimer, en fonction de la fréquence 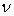 ,
la répartition à l’équilibre des photons dans l’enceinte.
,
la répartition à l’équilibre des photons dans l’enceinte.
5)1)b) Calculer la densité volumique spectrale d’énergie
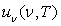 c’est à
dire l’énergie volumique des photons ayant leur fréquence comprise
entre
c’est à
dire l’énergie volumique des photons ayant leur fréquence comprise
entre  .
.
5)2) Etude thermodynamique
5)2)a) Calculer l’énergie interne volumique u des photons
de l’enceinte. en déduire l’énergie interne U.
5)2)b)
Calculer l’entropie S des photons de l’enceinte, leur énergie
libre F, la pression de radiation p ainsi que l’enthalpie libre
G.
5)3) Etude de la densité volumique spectrale d’énergie
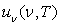
- pour les faibles fréquences (loi de Rayleigh-Jeans)
- pour les fréquences élevées (loi de Wien)
- représenter graphiquement
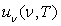 en fonction de la fréquence, pour une température donnée ;
calculer
en fonction de la fréquence, pour une température donnée ;
calculer 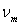 fréquence
correspondant à une valeur maximale de
fréquence
correspondant à une valeur maximale de 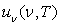
5)4) Flux de photons à travers un orifice. Constante
de Stefan-Boltzmann
- calculer, en fonction de la température, le nombre n de photons
par unité de volume dans l’enceinte
- calculer le nombre
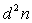 de photons par unité de volume ayant une direction de vitesse dans
un angle solide
de photons par unité de volume ayant une direction de vitesse dans
un angle solide 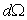
- en déduire le nombre de photons
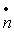 quittant l’enceinte par un orifice de section unitaire.
quittant l’enceinte par un orifice de section unitaire.
- A.N.
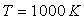
- montrer que le flux énergétique s’échappant de l’enceinte
est égale à
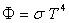 ;
calculer
;
calculer  constante
de Stefan-Boltzmann.
constante
de Stefan-Boltzmann.
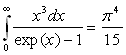 ;
;
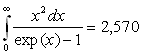
| Réponse
51a | Réponse
51b | Réponse
52a | Réponse
52b | Réponse
53 | Réponse
54 |
6) Statistique de Bose-Einstein : étude
de la capacité calorifique des solides
L’énergie interne dans un solide est due à la vibration,
autour de leur position d’équilibre, des particules constituant le solide.
A l’onde acoustique se propageant dans un solide, on peut associer une corpuscule
dénommée phonon de type boson. L’étude des propagations
des ondes acoustiques montrent que l’énergie d’un phonon est limitée
par une valeur maximale 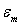 .
.
Ainsi les vibrations du réseau d’un solide sont représentées
par une assemblée de phonons de nombre indéterminé obéissant
à la statistique de Bose-Einstein. Le nombre d’états possibles
pour un phonon d’avoir une énergie comprise entre 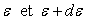 est égal à
est égal à 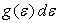 .
.
6)1) Capacité calorifique d’un solide pour une densité
d’états quelconque
6)1)a) Le réseau à trois dimensions étant
constitué de N atomes, écrire le nombre total d’états
possibles.
6)1)b) Ecrire les expressions théoriques donnant l’énergie
interne U et la capacité calorifique à volume constant
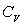 .
.
6)1)c)
Que deviennent ces expressions pour une température T élevée ?
Conclusion.
6)2) Modèle d’Einstein
Dans le modèle d’Einstein, 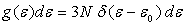 où
où 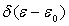 est
la distribution de Dirac [
est
la distribution de Dirac [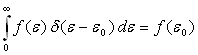 ].
Ce modèle revient à considérer que toutes les particules
vibrent à une fréquence unique égale à
].
Ce modèle revient à considérer que toutes les particules
vibrent à une fréquence unique égale à 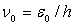 .
.
Calculer et représenter 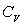 .
.
6)3) Modèle de Debye
D’une manière générale, l’onde acoustique
de fréquence  se propageant dans un solide est la superposition d’une onde longitudinale,
de vitesse de phase
se propageant dans un solide est la superposition d’une onde longitudinale,
de vitesse de phase  ,
de nombre d’onde
,
de nombre d’onde 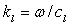 et de deux ondes transversales polarisées perpendiculairement entre elles
de vitesse de phase
et de deux ondes transversales polarisées perpendiculairement entre elles
de vitesse de phase 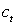 ,
de nombre d’onde
,
de nombre d’onde 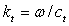 .
.
Le phonon associé à une onde acoustique obéit aux mêmes
relations de De Bröglie que le photon : 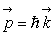 et
et  .
.
Dans ce modèle, on admet que l’énergie varie continûment
jusqu’à la valeur maximale 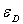 ,
et on néglige la dispersion dans le phénomène de propagation
(les vitesses de phase sont indépendantes de la fréquence).
,
et on néglige la dispersion dans le phénomène de propagation
(les vitesses de phase sont indépendantes de la fréquence).
6)3)1) Exprimer le nombre d’états possibles 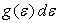 en considérant que chaque mode longitudinal ou transversal est indépendant.
en considérant que chaque mode longitudinal ou transversal est indépendant.
On posera :  .
.
6)3)2) A partir du nombre total d’états possibles, exprimer 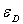 ainsi que la température de Debye
ainsi que la température de Debye 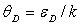 .
.
6)3)3) Donner les expressions théoriques de 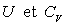 .
On envisagera les cas
.
On envisagera les cas 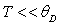 et
et  . Représenter
. Représenter
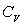 . Comparer les
résultats à ceux du modèle d’Einstein.
. Comparer les
résultats à ceux du modèle d’Einstein.
| Réponse
61a | Réponse
61b | Réponse
61c | Réponse
62 | Réponse
631 | Réponse
632 | Réponse
633 |
7) Statistique de Fermi-Dirac : étude
des propriétés des électrons
Les électrons d’un plasma et les électrons fortement
énergétiques d’un réseau solide (capables de se déplacer
dans tout le solide) sont le principal exemple de fermions c’est à dire
de particules obéissant à la statistique de Fermi-Dirac.
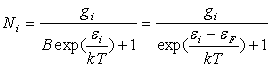 ou
ou 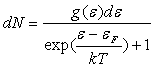 (pour un
continuum d’énergie).
(pour un
continuum d’énergie).
La quantité  est appelée énergie de Fermi. On montre que l’énergie
de Fermi dépend faiblement de la température. Elle sera supposée
constante sauf précision contraire.
est appelée énergie de Fermi. On montre que l’énergie
de Fermi dépend faiblement de la température. Elle sera supposée
constante sauf précision contraire.
7)1) Occupation des niveaux d’énergie
La fonction 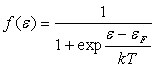 représente la probabilité d’occupation d'un niveau d'énergie
représente la probabilité d’occupation d'un niveau d'énergie
 .
.
Etudier cette fonction pour différentes valeurs de 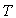 à partir de
à partir de 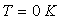 (on pourra poser
(on pourra poser 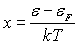 ).
).
Donner une expression linéarisée de 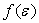 .
.
Conclusions sur la façon de remplir les différents niveaux d'énergie
(on distinguera le cas des isolants, des conducteurs et des semi-conducteurs).
| Réponse
71 |
7)2) Gaz d’électrons
On fait l’hypothèse que les électrons " libres "
du réseau se comportent comme les particules d’un gaz en mouvement de
translation. On rappelle que le spin d’un électron, à un même
niveau d’énergie, peut prendre deux valeurs.
7)2)a) Estimation de l’énergie de Fermi
- Calculer l’énergie de Fermi à 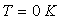 ,
puis à une température
,
puis à une température 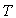 en prenant l’expression linéarisée de
en prenant l’expression linéarisée de 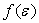 .
.
- A.N. pour le cuivre : 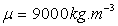 ;
;
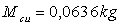 ; Nombre d’électrons
" libres " par atome : 1 ; masse de l’électron :
; Nombre d’électrons
" libres " par atome : 1 ; masse de l’électron :
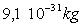
- A partir du calcul de  ,
montrer que la statistique de Maxwell-Boltzmann ne saurait être appliquée
aux électrons " libres " du cuivre solide.
,
montrer que la statistique de Maxwell-Boltzmann ne saurait être appliquée
aux électrons " libres " du cuivre solide.
7)2)b) Calculer l’énergie interne et la
capacité calorifique à volume constant du " gaz
d’électrons " [on limitera le calcul à l’expression
linéarisée de 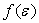 ]
]
| Réponse
72a | Réponse
72b |
7)3) Etude des propriétés des semi-conducteurs
|
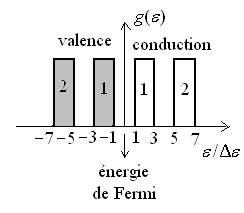
7)3)a) Bandes permises intervenantOn schématise
un semi-conducteur par une suite de bandes d’énergie permises toutes
identiques de largeur 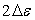 . Comme
indiqué sur la figure, l’énergie de Fermi est au centre
d’une bande interdite, elle sera prise comme origine de l’axe des énergies. . Comme
indiqué sur la figure, l’énergie de Fermi est au centre
d’une bande interdite, elle sera prise comme origine de l’axe des énergies.
A 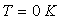 , les
bandes d’énergie négatives sont pleines (bandes de valence)
et celles positives sont vides (bandes de conduction). , les
bandes d’énergie négatives sont pleines (bandes de valence)
et celles positives sont vides (bandes de conduction).
La densité d’états possibles dans chaque bande permise est
supposée constante et égale à 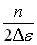
|
|
Calculer le rapport du nombre 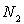 d’électrons dans la deuxième bande conduction sur le nombre
d’électrons dans la deuxième bande conduction sur le nombre 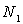 d’électrons dans la première.
d’électrons dans la première.
Calculer le rapport du nombre 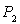 de trous dans la deuxième bande de valence sur le nombre
de trous dans la deuxième bande de valence sur le nombre 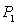 de trous dans la première.
de trous dans la première.
A.N. 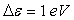 ;
;
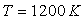
En déduire que, pour les semi-conducteurs, les calculs peuvent être
fait, en première approximation, avec une seule bande de conduction d’énergie
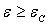 et avec une seule
bande de valence d’énergie
et avec une seule
bande de valence d’énergie 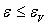 .
.
7)3)b) Fonctionnement d’un semi-conducteur non dopé
Une bonne approximation du nombre d’états possibles est l’approximation
parabolique au voisinage de 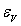 et de
et de 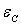 .
.
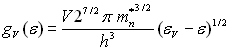 et
et 
- Montrer que la concentration (nombre par unité de
volume) en électrons dans la bande de conduction est donnée par
: 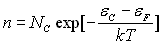 où
où
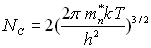 , celle en trous
est donnée par :
, celle en trous
est donnée par : 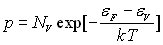 où
où 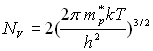
- Pour le fonctionnement intrinsèque d'un semi-conducteur,
la neutralité électrique impose 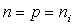 .
.
En déduire 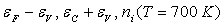 .
.
 . Montrer que
. Montrer que
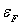 varie peu avec
la température.
varie peu avec
la température.
AN : Pour le Silicium, 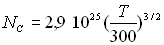 ;
; 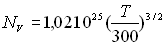 ,
, 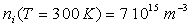 ;
;
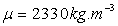 ;
; 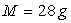
7)3)c) Fonctionnement d’un semi-conducteur dopé
7)3)c)a) Dans une situation
plus générale, on introduit des impuretés (semi-conducteur
dopé) c’est à dire des atomes donneurs (atomes pentavalents P,
As ou Sb) et accepteurs (atomes trivalents B, Al, Ga ou In) en concentrations
respectives 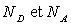 .
.
A une température quelconque, seule une fraction de ces atomes est ionisée,
soient 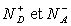 les concentrations
des ions ainsi formés
les concentrations
des ions ainsi formés
suivant le type de dopage, on comparera le nombre d’impuretés au nombre
d’atomes de Si).
7)3)c)b) Un semi-conducteur
est dopé à l'aide d'atomes donneurs en concentration 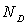 .
.
A la température 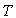 ,
supposée constante et de l'ordre de l'ambiante, on a
,
supposée constante et de l'ordre de l'ambiante, on a 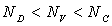 .
.
La densité d'atomes donneurs non ionisés vaut : 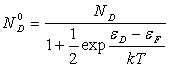 (
(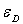 est l'énergie
du niveau donneur ;
est l'énergie
du niveau donneur ; 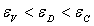 ).
).
- Déterminer l'expression de la concentration
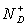 d'atomes donneurs
ionisés
d'atomes donneurs
ionisés
- Calculer 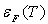 et
et 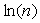 . Commenter.
. Commenter.
| Réponse
73a | Réponse
73b | Réponse
73ca | Réponse
73cb |
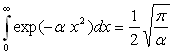
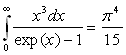 ;
;
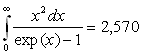
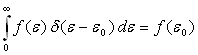 ].
Ce modèle revient à considérer que toutes les particules
vibrent à une fréquence unique égale à
].
Ce modèle revient à considérer que toutes les particules
vibrent à une fréquence unique égale à 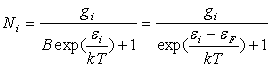 ou
ou 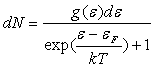 (pour un
continuum d’énergie).
(pour un
continuum d’énergie).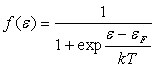 représente la probabilité d’occupation d'un niveau d'énergie
représente la probabilité d’occupation d'un niveau d'énergie

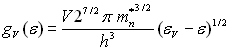 et
et 
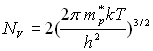
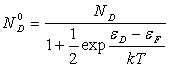 (
(