On considère une particule libre de masse m, d’énergie E dont l’état peut être décrit par la fonction
Exercices de physique quantique
1) Paquet d’ondes
On considère une particule libre de masse m, d’énergie
E dont l’état peut être décrit par la fonction ![]()
1)1) Soit une fonction d’onde ![]()
1)1)a) Donner la relation qui existe entre ![]() pour que
pour que ![]() soit
solution de l’équation de Schrödinger. En déduire la valeur
de l’énergie E en fonction de
soit
solution de l’équation de Schrödinger. En déduire la valeur
de l’énergie E en fonction de ![]() .
.
1)1)b) Calculer la densité de probabilité ![]() de la particule. L’état du système peut-il être décrit
par
de la particule. L’état du système peut-il être décrit
par ![]() ainsi définie ?
ainsi définie ?
1)2) On propose la fonction ![]() définie par :
définie par : 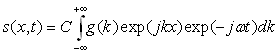 où
où ![]() est
une fonction du vecteur d’onde
est
une fonction du vecteur d’onde ![]() .
.
1)2)a) Justifier pourquoi ![]() est solution de l’équation de Schrödinger.
est solution de l’équation de Schrödinger.
![]() représente-t-elle
un état physique ?
représente-t-elle
un état physique ?
1)2)b) A ![]() ,
l’état du système est représenté par
,
l’état du système est représenté par ![]() .
.
Pour quelle valeur de C, ![]() est la transformée de Fourier de
est la transformée de Fourier de ![]() ?
?
Quelle condition doit satisfaire ![]() pour que
pour que ![]() soit
normalisable ?
soit
normalisable ?
| Réponse 11a | Réponse 11b | Réponse 12a | Réponse 12b |
2) Paquet d’ondes – Relation d’incertitude
2)1) Donner la forme générale de la fonction
d’onde d’une particule
2)2) La fonction d’onde, à l’instant ![]() ,
est donnée par :
,
est donnée par :
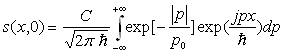 où
où ![]() est une constante positive et C une constante destinée à
normaliser la fonction
est une constante positive et C une constante destinée à
normaliser la fonction ![]() .
.
2)2)a) Quelle est la transformée de Fourier ![]() de
de ![]() . Interpréter
. Interpréter
![]() et
et![]() .
.
2)2)b) Calculer ![]() et représenter graphiquement
et représenter graphiquement ![]() et
et ![]() .
.
2)2)c) Supposons que ![]() et
et ![]() ne prennent
des valeurs appréciables que dans les intervalles respectifs
ne prennent
des valeurs appréciables que dans les intervalles respectifs ![]() et
et ![]() .
.
Que peut-on dire du produit ![]() ?
Interpréter
?
Interpréter ![]() ,
,
![]() et
et ![]() .
.
2)2)d) Quelle est la probabilité ![]() pour qu’une mesure de l’impulsion effectuée à l’instant
pour qu’une mesure de l’impulsion effectuée à l’instant ![]() ,
donne un résultat compris entre
,
donne un résultat compris entre ![]() ?
Etudier la fonction
?
Etudier la fonction ![]() .
.
2)2)e) Donner la fonction ![]() de la particule à l’instant t. Etudier la fonction probabilité
de la particule à l’instant t. Etudier la fonction probabilité
![]() . Interpréter.
. Interpréter.
| Réponse 21 | Réponse 22a | Réponse 22b | Réponse 22c | Réponse 22d | Réponse 22e |
3) Indice d’un cristal en optique électronique
– Diffraction d’un électron par un réseau cristallin – Loi de
Bragg et écart à la loi de Bragg
Dans un monocristal, on peut grouper les atomes par familles de plans,
appelés plans réticulaires, parallèles et équidistants.
Un faisceau parallèle monochromatique d’électrons d’énergie
cinétique ![]() pénètre
dans le monocristal, l’angle d’incidence avec la normale aux plans réticulaires
est noté
pénètre
dans le monocristal, l’angle d’incidence avec la normale aux plans réticulaires
est noté ![]() .
.
|
On caractérise l’interaction d’un électron
avec les ions du cristal par l’énergie potentielle 3)1) Quelle est l’expression de n en fonction
de |
|
3)2) Montrer que l’accord de phase entre les ondes (1)
et (2) [direction privilégiée où le flux d’électrons
est maximum] se traduit par la relation :
![]() où k
est un entier et l la longueur d’onde associée
à l’électron incident.
où k
est un entier et l la longueur d’onde associée
à l’électron incident.
3)3) Montrer que, si on néglige la réfraction
du rayon (2), on trouve la relation de Bragg ![]()
3)4) A.N. ![]() ;
;
![]() ;
; ![]() ;
;
![]()
| Réponse 31 | Réponse 32 | Réponse 33 | Réponse 34 |
4) Réflexion de particules sur un mur de potentiel
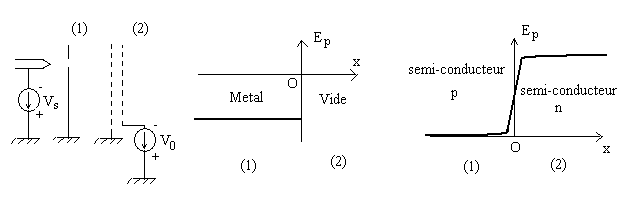
En ![]() ,
la particule rencontre une barrière de potentiel d’énergie
,
la particule rencontre une barrière de potentiel d’énergie ![]() .
Dans le milieu (1), la particule possède une énergie cinétique
.
Dans le milieu (1), la particule possède une énergie cinétique
![]() , l’énergie
potentielle sera prise de référence dans ce milieu (
, l’énergie
potentielle sera prise de référence dans ce milieu (![]() ).
).
4)1) Etude des cas physiques possibles dans le cadre de la mécanique classique.
4)2) Etude des cas physiques possibles dans le cadre de la mécanique quantique.
| Réponse 41 | Réponse 42 |
5) Traversée d’une barrière de potentiel. Effet tunnel
|
Dans les milieux (1) et (3), la particule possède
une énergie cinétique |
|
5)1) Il s’agit de calculer, au sens quantique, la possibilité de traversée de la barrière de potentiel (effet tunnel) c’est à dire le facteur de transmission T, rapport du flux de particules atteignant la partie (3) sur le flux de particules incidentes dans la partie (1).
Trouver une formule approchée si 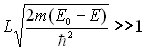 .
.
| Réponse 51 |
2) Radioactivité a - Loi de Gamow, Condon et Gurney
|
L’énergie potentielle d’une particule a
dans un noyau radioactif a la forme représentée ci-contre.
Pour 2)a) Exprimer la constante K sachant que
le nombre de protons du noyau est Z. Dans la suite, on considérera
le cas concret de l’Uranium 238 où |
|
une énergie E comprise entre ![]() ,
établir la formule de Gamow, Condon et Gurney :
,
établir la formule de Gamow, Condon et Gurney :
![]() où T
est le facteur de transmission pour atteindre
où T
est le facteur de transmission pour atteindre ![]() défini par
défini par ![]() .
.
On admettra pour établir cette relation que localement on peut appliquer
la formule approchée établie en 1) et que ![]() est très inférieur à 1.
est très inférieur à 1.
A.N. Calculer T si ![]() .
.
| Réponse 52a | Réponse 52b |
3) Emission électronique par effet tunnel ou émission froide
|
On applique un champ électrique uniforme |
|
| Réponse 53a | Réponse 53b |
6) Etude d’un puits de potentiel carré
|
Une particule non relativiste se déplace suivant
un axe Ox. L’énergie potentielle 6)1) Etude des cas physiques possibles dans le cadre de la mécanique classique. 6)2) Etude des cas physiques possibles dans le cadre de la mécanique quantique. |
|
| Réponse 61 | Réponse 62 |
7) Etude d’un puits de potentiel infini
Puits de potentiel unidimensionnel
|
On considère le potentiel 7)1) Pour une particule non relativiste, montrer
que les énergies possibles |
|
Calculer les fonctions d’onde possibles ![]() correspondantes ; normaliser ces fonctions.
correspondantes ; normaliser ces fonctions.
7)2) L’état décrivant la particule à
l’instant ![]() est :
est :
![]()
7)2)a) Quelle est la probabilité lorsqu’on mesure l’énergie
de la particule de trouver une valeur inférieure à ![]() .
.
7)2)b) Déterminer la matrice représentative de l’opérateur
position x dans la base ![]()
7)2)c) Calculer,
![]() ainsi que
ainsi que ![]()
En
déduire ![]() .
Conclusion.
.
Conclusion.
7)3) Puits de potentiel tridimensionnel
On considère le potentiel ![]() défini par la fonction :
défini par la fonction :
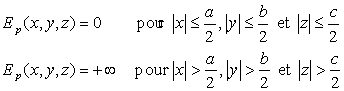
Pour une particule non relativiste, montrer que les énergies
possibles ![]() sont
quantifiées ; Quel est le degré de dégénérescence
entre les niveaux d’énergie
sont
quantifiées ; Quel est le degré de dégénérescence
entre les niveaux d’énergie ![]() dans
l’approximation où le spectre d’énergie est quasi continu ?
dans
l’approximation où le spectre d’énergie est quasi continu ?
Calculer les fonctions d’onde possibles ![]() correspondantes ; normaliser ces fonctions.
correspondantes ; normaliser ces fonctions.
| Réponse 71 | Réponse 72a | Réponse 72b | Réponse 72c | Réponse 73 |
8) Potentiel périodique : modèle de Krönig-Penney
|
Le modèle unidimensionnel simplifié ci-contre représente celui d’un électron à l’intérieur d’un cristal. 8)1) Pour déterminer les fonctions d’onde
possible, on cherche une solution (fonction de Bloch) sous la forme :
|
|
Montrer qu’on obtient des fonctions d’onde possibles si :
- pour ![]() ,
,
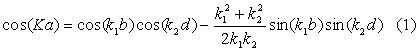 avec
avec 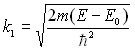 et
et 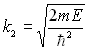
- pour ![]() ,
,
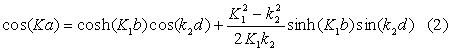 avec
avec 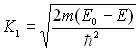 et
et 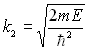
8)2) On se propose d’étudier les équations
(1) ou (2).
8)2)a) Montrer que les valeurs de K peuvent être limitées
à l’intervalle ![]() .
Cette représentation est connue sous le nom de zone réduite
de Brillouin.
.
Cette représentation est connue sous le nom de zone réduite
de Brillouin.
8)2)b) On limite l’étude au cas où ![]() et
et ![]() avec
avec ![]()
Montrer que l’équation (2) devient :
![]() avec
avec ![]()
8)2)c) A quels cas physiques correspondent les valeurs ![]() et
et ![]()
Représenter la fonction ![]() pour un valeur quelconque de P ainsi que pour ses valeurs extrêmes.
pour un valeur quelconque de P ainsi que pour ses valeurs extrêmes.
Conclusion.
| Réponse 81 | Réponse 82a | Réponse 82b | Réponse 82c |
9) Oscillateur harmonique à une dimension
L’énergie
potentielle d’une particule de masse m est donnée par ![]() où x représente, pour la particule, l’écart à
sa position d’équilibre.
où x représente, pour la particule, l’écart à
sa position d’équilibre.
1) Ecrire l’équation de Schrödinger pour des états stationnaires
2)
2)a) Vérifier que la fonction ![]() correspond à un état stationnaire possible. On déterminera
a en fonction de
correspond à un état stationnaire possible. On déterminera
a en fonction de 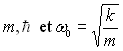 ;
en déduire l’énergie
;
en déduire l’énergie ![]() correspondant à cet état.
correspondant à cet état.
2)b) Calculer la constante A pour que la fonction ![]() soit normée (
soit normée ( .
.
2)c)
Comparer résultat quantique et résultat classique.
3) On définit les opérateurs :
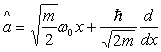 et
et 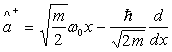
3)a) Montrer que :
![]() et
et ![]() où
H est l’hamiltonien.
où
H est l’hamiltonien.
3)b) On considère la fonction ![]() .
.
Calculer ![]() en fonction
de
en fonction
de ![]()
En déduire ![]() en fonction de
en fonction de ![]()
3)c) Montrer que ![]() est un nouvel état stationnaire possible et exprimer son énergie
est un nouvel état stationnaire possible et exprimer son énergie
![]() en fonction de
en fonction de
![]() .
.
3)d) En déduire l’expression générale ![]() de l’énergie des états stationnaires possibles.
de l’énergie des états stationnaires possibles.
| Réponse 91 | Réponse 92a | Réponse 92b | Réponse 92c | Réponse 93a | Réponse 93b | Réponse 93c | Réponse 93d |
10) Problème à deux corps
On considère deux particules de masses ![]() et
et ![]() en interaction
situées aux points
en interaction
situées aux points ![]() et
et ![]() définis
par
définis
par
![]() et
et ![]() .
.
![]()
L’énergie potentielle d’interaction entre les particules
est notée ![]() .
.
L’équation de Schrödinger, pour les deux particules
dans le référentiel galiléen d’origine O s’écrit :
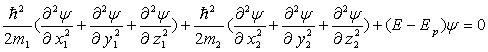
Ecrire l’équation de Schrödinger à partir
des coordonnées (![]() )
et (
)
et (![]() ) définies
par
) définies
par 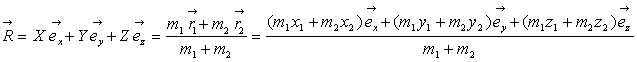
Conclure.
| Réponse |
11) Etude de l’atome d’hydrogène
Il s’agit d’étudier la fonction d’onde ![]() pour une particule de masse réduite
pour une particule de masse réduite ![]() soumise à une interaction proton-électron
soumise à une interaction proton-électron 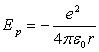 .
.
![]() ð
ð ![]() d’une part, le barycentre se confond avec la position du proton d’autre part.
d’une part, le barycentre se confond avec la position du proton d’autre part.
|
L’étude est menée en coordonnées sphériques.
|
|
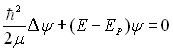 ð
ð 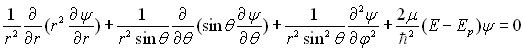
11)1)a) Ecrire les composantes ![]() du moment cinétique
du moment cinétique ![]() ainsi que les opérateurs associés en coordonnées cartésiennes
et en coordonnées sphériques.
ainsi que les opérateurs associés en coordonnées cartésiennes
et en coordonnées sphériques.
11)1)b) Ecrire, en coordonnées sphériques, l’opérateur
associé à ![]() .
Réécrire l’équation de Schrödinger en introduisant
cet opérateur.
.
Réécrire l’équation de Schrödinger en introduisant
cet opérateur.
11)2)a) Calculer les valeurs propres de ![]()
11)2)b) Calculer les valeurs propres de ![]()
11)3) Résolution de l’équation de Schrödinger
11)3)a) On cherchera une solution à variables séparées
sous la forme ![]()
On montrera,
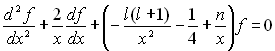 si
si 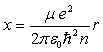 et
et 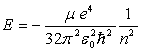
11)3)b)
Chercher les solutions asymptotiques (pour ![]() )
de la fonction
)
de la fonction ![]() et montrer que si on pose
et montrer que si on pose ![]() ,
on obtient l’équation différentielle
,
on obtient l’équation différentielle![]()
11)3)c)
On cherche pour ![]() une solution sous la forme d’une série entière, soit
une solution sous la forme d’une série entière, soit ![]()
Etablir la relation ![]() .
.
Montrer que, pour k suffisamment grand, ![]() ð
ð ![]()
![]() ð
ð
![]()
En déduire, après étude de la fonction
![]() , que
, que ![]() ne peut être une série infinie.
ne peut être une série infinie.
11)3)d)
La série ![]() est limitée au terme k par la condition
est limitée au terme k par la condition ![]() qui impose à n d’être entier. Les polynômes ainsi
obtenus sont appelés polynômes de Laguerre.
qui impose à n d’être entier. Les polynômes ainsi
obtenus sont appelés polynômes de Laguerre.
Pour un niveau d’énergie  ,
calculer le nombre de fonctions
,
calculer le nombre de fonctions ![]() correspondantes (dégénérescence).
correspondantes (dégénérescence).
Ecrire les différentes fonctions ![]() pour
pour ![]() (on posera
(on posera
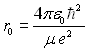 )
)
| Réponse 111a | Réponse 111b | Réponse 112a | Réponse 112b | Réponse 113a | Réponse 113b | Réponse 113c | Réponse 113d |