Théorie de la Relativité
Plan
1. Introduction
1.1. L'expérience de Michelson et Morley (1887)
1.2. Les postulats de la Relativité (Einstein
1905)
2. Relativité restreinte
2.1. La transformation de Lorentz
2.2. Quadrivecteur
2.3. Quadrivecteur position-temps
2.4. Temps propre
2.5. Equations de Maxwell en Relativité
2.6. Dynamique relativiste
2.7. Quadrivecteur impulsion-énergie
3. Relativité générale
1. Introduction
La propagation des ondes électromagnétiques fait apparaître
l’opérateur  appelé D’Alembertien où
appelé D’Alembertien où 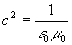 représente la vitesse de propagation de l’ondes dans le vide.
représente la vitesse de propagation de l’ondes dans le vide.
Dans les milieux matériels, la vitesse de propagation est au
maximum égale à celle dans le vide.
Lors de l’établissement des équations de propagation
de l’onde électromagnétique, nous ne nous sommes pas préoccupés
de définir le référentiel (ou les référentiels)
de validité et ceci est, en soi, étrange comparé à
la démarche scientifique liée à la Mécanique
et à la cinématique.
Or l’application de la transformation de Galilée à l’opérateur
D’Alembertien change sa forme c’est à dire que les équations
de propagations de l’électromagnétisme (plus généralement
les équations de Maxwell) ne sont pas covariantes dans la transformation
de Galilée.
Deux attitudes sont possibles :
- les équations de Maxwell ne sont valables que dans un référentiel
de l’univers (appelé " éther ") qui se distingue de tous
les autres par le fait que la vitesse de propagation des ondes électromagnétiques
dans le vide y est égale à c ; si, tel est le cas
et contrairement à la Mécanique, il est alors possible par
une expérience d’électromagnétisme de mettre en évidence
le mouvement des référentiels galiléens les uns par
rapport aux autres et, en particulier par rapport à " l’éther
",
- les équations de Maxwell sont valables dans tous les référentiels
galiléens et satisfont au principe de l’invariance galiléenne
; la transformation de Galilée n’est pas valable pour l’électromagnétisme.
1.1. L’expérience de Michelson et Morley
(1887)
Son but est d’essayer de détecter un mouvement de la Terre par
rapport à " l’éther ".
Rappelons que la Terre décrit, en 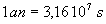 ,
une orbite quasi circulaire autour du Soleil d’un rayon égal à
,
une orbite quasi circulaire autour du Soleil d’un rayon égal à 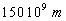 ce qui correspond à une vitesse de la Terre sur son orbite de
ce qui correspond à une vitesse de la Terre sur son orbite de 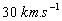 .
.
Dans sa rotation propre, la vitesse au sol au niveau de l’équateur est
de 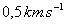 .
.
Si l’éther existe, il est impensable qu’il soit lié à
la Terre. A la limite, on peut admettre une immobilité accidentelle,
à un instant donné, de la Terre par rapport à " l’éther
" mais elle ne saurait se maintenir dans le temps.
 |
En B et C sont placés des miroirs totaux
et en A un miroir semi réfléchissant.
Les bras AB, AC sont placés parallèlement ou à
la perpendiculaire de la direction de la vitesse de la Terre sur son orbite
autour du Soleil.
Pendant la durée d’une expérience, on peut considérer
que cette vitesse est uniforme. |
Quelque soit la position des bras de l’interféromètre, Michelson
et Morley constate que la figure d’interférences n’est pas modifiée.
A leur époque, il pouvait détecter des vitesses de l’ordre  .
.
Ainsi, à moins d’admettre que " l’éther " se confond
avec un référentiel lié à la Terre, il faut
admettre que les ondes électromagnétiques n’obéissent
pas aux règles de la cinématique classique ou que les équations
de Maxwell sont à revoir.
1.2. Les postulats de la Relativité (Einstein
1905)
Postulat 1 ou principe de l’invariance galiléenne : les
résultats de toute expérience (mécanique ou électromagnétique)
conduite à l’intérieur d’un référentiel sont
indépendants de tout mouvement de translation rectiligne uniforme
de ce référentiel par rapport à un référentiel
galiléen.
(On rappelle qu’un référentiel est galiléen
si le mouvement d’un objet ponctuel isolé est rectiligne, uniforme
et que les référentiels galiléens sont en translation
rectiligne, uniforme les uns par rapport aux autres).
Suivant ce postulat, les lois de la Physique sont covariantes (se traduisent
par des relations ayant même structure) dans un changement de référentiel
galiléen et la transformation de changement de référentiel
galiléen est unique pour la Physique.
Compte tenu des résultats de l’expérience de Michelson
et Morley, on doit renoncer à la transformation de Galilée.
Postulat 2 : la vitesse de propagation de l’onde électromagnétique
dans le vide est invariante vis à vis d’un changement de référentiel
galiléen, elle est égale à 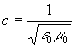 .
.
Postulat 3 : le succès de la Mécanique appliquée
à des corps macroscopiques animés de faibles vitesses, succès
qui se concrétise dans le domaine astronomique par une précision
extraordinaire, montre que les lois de la Mécanique classique et
la transformation de Galilée doivent être valables, en première
approximation, lorsque les vitesses restent faibles devant c.
Postulat 4 : la masse m, la charge q d’une particule
sont propres à celle-ci c’est à dire invariantes par changement
de référentiel galiléen
Le postulat 1, en généralisant la notion d’invariance
galiléenne, impose un cadre commun aux théories de la Mécanique
et à celles de l’Electromagnétisme ; le postulat 2, fondamentalement
nouveau, a une conséquence d’une portée considérable
: l’abandon de l’hypothèse de temps absolu.
Montrons le sur un exemple.
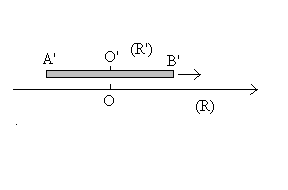 |
Une barre A’B’ de milieu O’ est fixe dans un
référentiel galiléen (R’) animé d’un mouvement
de translation rectiligne uniforme par rapport à un autre référentiel
(R).
En A’ et B’ sont placés des expérimentateurs munis de
lampes. En O’ et en un point O du référentiel (R) se trouvent
des observateurs.
Lorsque les points O et O’ coïncident, les deux observateurs en
O et O’ voient les expérimentateurs allumer leur lampe en même
temps. |
Demandons nous, en adoptant le point de vue de chaque observateur, qui
de l’expérimentateur placé en A’ ou de celui en B’ a allumé
sa lampe le premier.
Dans chacun des référentiels, la vitesse de propagation
de la lumière est c.
Pour l’observateur placé en O’ milieu de A’B’, la réponse
est claire, les expérimentateurs en A’ et B’ ont allumé leurs
lampes en même temps.
Pour l’observateur placé en O, compte tenu des temps de propagation,
A’ était plus éloigné de O que B’, l’expérimentateur
en A’ a allumé sa lampe en premier.
Les deux évènements (allumer une lampe) simultanés
dans (R’) ne le sont pas dans (R).
On ne peut attribuer dans tous les référentiels galiléens
les mêmes dates aux mêmes évènements.
L’existence d’un temps dit absolu, indépendant du référentiel,
suppose des temps de propagation nuls c’est à dire des vitesses de propagation
infinies.
Cela ne peut exister dans des phénomènes électromagnétiques
(interaction coulombienne) puisque c, vitesse de propagation de l’onde
électromagnétique dans le vide, est une vitesse maximale.
Au sens de l'invariance galiléenne (postulat
1), cela ne peut être vrai en Mécanique et il découle que
l’interaction gravitationnelle dans le vide se propage à vitesse c.
La vitesse c interprétée, jusqu'à présent
comme vitesse de la lumière dans le vide (milieu où cette vitesse
est maximale) doit être comprise comme vitesse d'une interaction quelconque,
d'origine électromagnétique ou mécanique, dans le vide
(milieu où la vitesse de propagation de l'interaction est maximale).
Puisque c est la plus grande vitesse possible de propagation d’une interaction
(information) et que cette vitesse a une valeur finie, nous ne voyons jamais
un corps tel qu’il est mais tel qu’il était au moment où l’interaction
qui nous informe l’a quitté.
Nous ne pouvons pas déterminer la position d’un corps dans l’espace,
nous pouvons déterminer l’événement qui lui est lié
dans l’espace-temps.
Un événement est relaté par sa position et son
temps (x, y, z, t) dans le référentiel galiléen
où on l’examine.
L’exemple ci-dessus pour montrer la nécessité d’abandon
de l’hypothèse de temps absolu n’exige pas d’efforts de compréhension
particuliers. Certains trouveront que le raisonnement était simple,
presque évident et pourtant, à cause de ce qu’il induit,
on peut parler de révolution dans le monde des idées directrices
de la Physique.
2. Relativité restreinte
La théorie de la Relativité restreinte se limite aux seuls
référentiels galiléens, excluant les effets d’accélération
des référentiels. En fait, on doit exclure en Relativité
restreinte l’interaction gravitationnelle qui entre dans le cadre de la
Relativité générale.
2.1. La transformation de Lorentz
 |
(R) et (R’) sont deux référentiels galiléens,
les directions Ox et O’x’ coïncident. On règle les horloges
de chaque référentiel de telle sorte que, pour 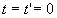 ,
les origines O et O’ soient confondus. ,
les origines O et O’ soient confondus. |
Le problème posé est celui de la correspondance d’un
même événement dans deux référentiels.
Illustrons le propos sur le cas de la propagation de l’onde électromagnétique.
Au temps 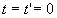 ,
une source émet une onde électromagnétique en
,
une source émet une onde électromagnétique en  .
.
Dans le référentiel (R), au temps t, elle atteint le point
de coordonnées ( ).
Ce même événement se traduit, dans le référentiel
(R’), par les coordonnées (
).
Ce même événement se traduit, dans le référentiel
(R’), par les coordonnées (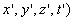 .
.
Dans chacun des référentiels, l’onde se propage à
vitesse
c et nous pouvons écrire :
 (1)
(1)
La linéarité des équations du mouvement d’une particule
libre dans un référentiel galiléen, la linéarité
des équations de la transformation de Galilée qui doivent être
vérifiées si la vitesse du référentiel (R’) par
rapport au référentiel (R) reste faible devant la vitesse c
incitent à chercher une solution linéaire au problème du
passage du référentiel (R) au référentiel (R’),
soit :  ,
,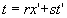 avec évidemment
avec évidemment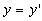 et
et 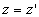 (2).
(2).
Ces équations permettent d’exprimer la vitesse de O’ par rapport à
(R) :  et
celle de O par rapport à (R’) :
et
celle de O par rapport à (R’) : 
En portant les équations (2) dans les équations (1) et en identifiant,
on obtient : 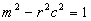 ,
, 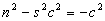 et
et  .
.
A partir de ces dernières équations, on obtient  ,
,
ð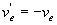 ,
donc
,
donc  ;
;  ;
; 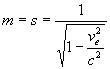 .
.
|
La transformation de Lorentz s’écrit :
|
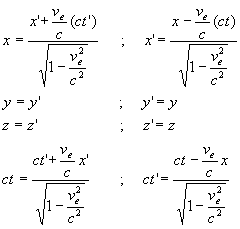 |
où souvent on pose  et
et 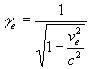 .
.
Remarques importantes :
- la " démonstration " faite de la transformation de Lorentz
n’a aucune généralité, son mérite est sa simplicité,
- évidemment, si 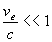 ,
on retrouve la transformation de Galilée,
,
on retrouve la transformation de Galilée,
- enfin (sans démonstration) on montre que les équations
de Maxwell sont covariantes dans la transformation de Lorentz.
Preuves expérimentales à posteriori
Mesure de la vitesse produite par une source en mouvement
Une preuve directe de l’indépendance de la vitesse de la lumière
vis à vis du mouvement de la source a été fournie par la
mesure de la vitesse de photons  provenant de la désintégration de mésons
provenant de la désintégration de mésons 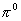 (CERN Genève 1964).
(CERN Genève 1964).
Grâce à un accélérateur, les mésons 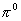 sont animés dans le référentiel du laboratoire d’une vitesse
sont animés dans le référentiel du laboratoire d’une vitesse  (énergie
(énergie ).
En se désintégrant en vol, ces mésons donnent naissance
à des photons
).
En se désintégrant en vol, ces mésons donnent naissance
à des photons  dont la vitesse est mesurée dans le référentiel du laboratoire
en déterminant leur temps de parcours sur une distance connue
dont la vitesse est mesurée dans le référentiel du laboratoire
en déterminant leur temps de parcours sur une distance connue  .
.
La vitesse des photons  ,
quelque soit leur direction, que l’on mesure ainsi est
,
quelque soit leur direction, que l’on mesure ainsi est 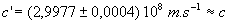 à
la précision des mesures confirme le postulat 2.
à
la précision des mesures confirme le postulat 2.
Existence d’une vitesse limite pour les particules
En 1964, W. Bertozzi a mis au point une expérience simple destinée
à mettre en évidence un désaccord flagrant entre la
mécanique classique et l’expérience.
L’idée consiste à mesurer à la fois l’énergie cinétique
E et la vitesse v et à tracer le graphe représentant
E en fonction de  .
.
Suivant la Mécanique classique, ce graphe doit conduire à
une droite.
L’expérience montre que, si le rapport 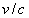 n’est pas faible devant l’unité, la courbe expérimentale s’éloigne
très nettement d’une droite et que l’énergie E continue
à croître alors que v tend asymptotiquement vers une valeur
limite égale à c.
n’est pas faible devant l’unité, la courbe expérimentale s’éloigne
très nettement d’une droite et que l’énergie E continue
à croître alors que v tend asymptotiquement vers une valeur
limite égale à c.
La Mécanique relativiste expliquera parfaitement ces résultats.
Autre forme de la transformation de Lorentz
 ;
; 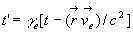 équations qui ne font pas explicitement appel à un système
de coordonnées.
équations qui ne font pas explicitement appel à un système
de coordonnées.
2.2. Quadrivecteur
Définition : dans un espace à quatre dimensions, appelé
espace de Minkowski, 4 grandeurs (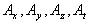 )
forment un quadrivecteur si elles se transforment suivant la transformation
de Lorentz.
)
forment un quadrivecteur si elles se transforment suivant la transformation
de Lorentz.
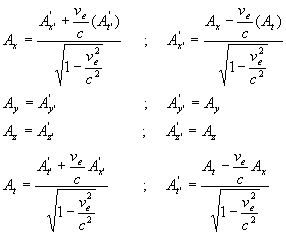 |

est une notation habituelle pour un quadrivecteur
|
Norme d’un quadrivecteur :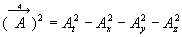
Cette quantité est invariante par changement de référentiel
galiléen [  ]
]
Produit scalaire :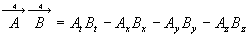
Cette quantité est invariante par changement de référentiel
galiléen.
Combinaison linéaire de deux quadrivecteurs : soient a
et b deux scalaires, 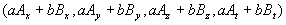 sont les composantes du quadrivecteur
sont les composantes du quadrivecteur  .
.
Différentielle d’un quadrivecteur :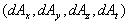 sont les composantes du quadrivecteur
sont les composantes du quadrivecteur 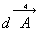 .
.
2.3. Quadrivecteur Position-temps
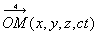 est le quadrivecteur
position-temps
est le quadrivecteur
position-temps
Simultanéité et localisation
Soient deux évènements repérés par les quadrivecteurs
position-temps 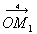 et
et  .
.
 est un quadrivecteur noté
est un quadrivecteur noté  ð
ð ;
; 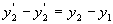 ;
;  ;
; 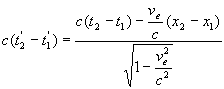
cas 1 : Dans (R), les deux évènements se produisent
en un même lieu, à des temps différents.
ð ;
; 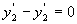 ;
;  ;
; 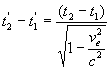
Dans (R’), les deux évènements ne se produisent pas au
même endroit (ceci n’est pas, en soi, nouveau : dans un référentiel
lié à un objet, ce dernier est toujours au même endroit
; dans un référentiel où il apparaît en mouvement,
il sera dans des endroits différents au cours du temps).
cas 2 : Dans (R), les deux évènements se produisent
au même temps dans des endroits différents.
ð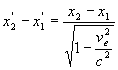 ;
;  ;
; 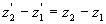 ;
; 
Dans (R’), les évènements se produisent dans des endroits
différents et, c’est fondamentalement nouveau, en des temps différents.
Contraction des longueurs
Soit un solide fixe dans (R’), ses dimensions sont 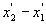 ,
,  et
et 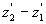 .
.
Dans (R) où le solide est en mouvement suivant la direction
x,
les repérages doivent être faits à un même instant
suivant cette direction.
ð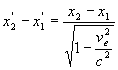 ;
;  ;
; 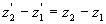
Il y a contraction des longueurs dans le sens du mouvement et
conservation des longueurs dans des directions perpendiculaires au mouvement.
Remarque : nous noterons (R0) le référentiel
où un objet, une particule est fixe ; les relations ci-dessus pourront
être écrites, pour des dimensions élémentaires 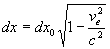 ,
, 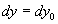 et
et  .
.
2.4. Quadrivecteur  .
Temps propre
.
Temps propre
On note 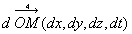 le quadrivecteur différentiel du quadrivecteur position-temps.
le quadrivecteur différentiel du quadrivecteur position-temps.
L’invariance de la norme d’un quadrivecteur permet d’écrire
:
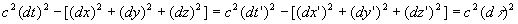 où, dans
le référentiel (R0), le temps,
appelé temps propre, est noté
où, dans
le référentiel (R0), le temps,
appelé temps propre, est noté 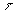 .
.
Dans le référentiel (R0), l’évènement
ne change pas de position ; dans le référentiel (R), les coordonnées
de l’événement ont varié de (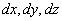 )
pendant le temps
)
pendant le temps 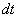 .
.
Ainsi 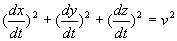 est
le carré de la vitesse d’une particule, liée au référentiel
(R0), exprimée dans le référentiel
(R).
est
le carré de la vitesse d’une particule, liée au référentiel
(R0), exprimée dans le référentiel
(R).
Par suite, 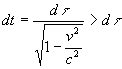 il y a dilatation du temps.
il y a dilatation du temps.
Au début de la relativité, ce phénomène
a donné lieu à un certain nombre d’objections (paradoxe des
jumeaux). Aujourd’hui, la situation est très différente puisque,
grâce à l’étude de la désintégration
des muons produits dans la haute atmosphère ou au comportement des
particules dans les accélérateurs, la dilatation du temps
est devenu un phénomène observé.
Compositions des vitesses
2.5. Equations de Maxwell en Relativité
Nous avons noté que les équations de Maxwell sont covariantes
dans la transformation de Lorentz. Cela prouve que ce sont des équations
possibles, seule l’expérience les confirme.
Quadrivecteur densité de courant
Un élément de volume  lié au repère (R0) contient un
certain nombre de charges élémentaires dont la charge est
lié au repère (R0) contient un
certain nombre de charges élémentaires dont la charge est 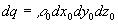 en introduisant la densité volumique de charges
en introduisant la densité volumique de charges 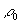 .
.
Dans le référentiel (R), l’invariance de charges (postulat
4) conduit à :
 , soit
, soit 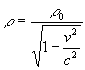
On définit le quadrivecteur densité de courant par la
relation 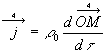 .
.
En remplaçant dans la définition, on trouve les composantes du
quadrivecteur  où apparaît le vecteur densité de courant.
où apparaît le vecteur densité de courant.
La norme de ce quadrivecteur est égale à 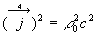 .
.
On remarquera que les composantes du quadrivecteur densité de courant
apparaissent dans l’expression de la conservation de la charge 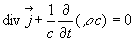 .
.
Quadrivecteur potentiel
Les équations de propagation du potentiel vecteur 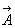 et du potentiel scalaire V s’écrivent :
et du potentiel scalaire V s’écrivent :
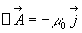 et
et  .
.
Nous avons dit que l’opérateur D’Alembertien était covariant,
si bien que les quatre composantes (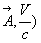 forment, comme (
forment, comme ( ),
un quadrivecteur.
),
un quadrivecteur.
Ce quadrivecteur est appelé quadrivecteur potentiel, il est noté  .
.
La relation de jauge de Lorentz 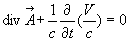 ,
de même forme que la relation de conservation de la charge, fait apparaître
identiquement les composantes du quadrivecteur potentiel.
,
de même forme que la relation de conservation de la charge, fait apparaître
identiquement les composantes du quadrivecteur potentiel.
2.6. Dynamique relativiste
Principe fondamental
En Mécanique classique, le principe fondamental de la dynamique, dans
un référentiel galiléen, s’écrit : 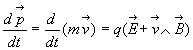 pour les forces électromagnétiques.
pour les forces électromagnétiques.
En Dynamique relativiste, ce principe doit satisfaire deux exigences
: il doit être covariant dans la transformation de Lorentz, il doit
redonner dans le cas de particules animées de faibles vitesses le
principe fondamental de la Mécanique classique.
Einstein a montré que ces deux exigences sont réalisées
en donnant une nouvelle définition à la quantité de mouvement,
à savoir : 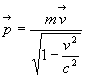 .
.
Souvent, on réserve le nom d’impulsion à cette
nouvelle définition.
Ecrite sous cette nouvelle forme 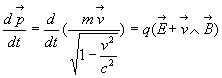 ,
la loi est possible, seule l’expérience la confirme.
,
la loi est possible, seule l’expérience la confirme.
Energie d’une particule
Comme en Mécanique classique, l’énergie cinétique est
définie par la relation 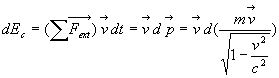
L’intégration de cette relation conduit à  .
.
Pour calculer la constante d’intégration, nous posons que l’énergie
cinétique est nulle si la particule est au repos,ð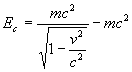 .
.
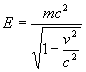 est l’énergie
de la particule.
est l’énergie
de la particule. 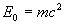 est appelée énergie propre ou énergie au repos
de la particule et traduit une équivalence entre l’énergie
et la masse.
est appelée énergie propre ou énergie au repos
de la particule et traduit une équivalence entre l’énergie
et la masse.
C’est une énergie associée à la seule masse
m
en l’absence de tout mouvement.
Elle constitue l’un des apports les plus originaux et les plus remarquables
de la Relativité puisque, dans les réactions nucléaires
mettant en jeu des collisions inélastiques, cette énergie
permet la création de nouvelles particules.
Théorème de l’énergie
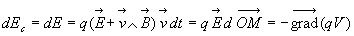 ð
ð
Remarques : 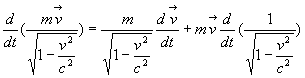 ,
,
- soumise à un champ unique de type magnétique, l’énergie
d’une particule reste constante (ð l’intensité
de vitesse reste constante) et 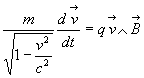 ,
,
- pour une direction de vitesse unique, on obtient 
Parce qu’il apparaît des formes telles que  ,
certains se croient obliger de parler de masse variant avec la vitesse (donc
aussi, de masse au repos), de masse transversale ou de masse longitudinale.
Ce langage ne présente aucun intérêt, pire certains y voient
quelques explications pseudoscientifiques.
,
certains se croient obliger de parler de masse variant avec la vitesse (donc
aussi, de masse au repos), de masse transversale ou de masse longitudinale.
Ce langage ne présente aucun intérêt, pire certains y voient
quelques explications pseudoscientifiques.
2.7. Quadrivecteur impulsion-énergie
 est un quadrivecteur
dont les composantes sont
est un quadrivecteur
dont les composantes sont 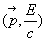 .
Il est appelé quadrivecteur impulsion-énergie, notation
.
Il est appelé quadrivecteur impulsion-énergie, notation 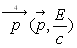 .
.
La norme de ce quadrivecteur est : 
Cas du photon
Le photon, particule associée à la l’onde électromagnétique,
se propage dans le vide à la vitesse c. L’expression de l’énergie
d’une particule montre que sa masse est nécessairement nulle.
Nous savons qu’un photon associé à une onde électromagnétique
de fréquence 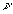 (pulsation
(pulsation 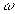 )
a une énergie
)
a une énergie 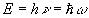 .
.
L’expression de la norme du quadrivecteur impulsion-énergie permet de
calculer l’expression de l’impulsion 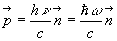 où
où 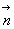 est le vecteur unitaire porté par la direction de propagation du photon
[
est le vecteur unitaire porté par la direction de propagation du photon
[ 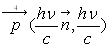 ].
].
Réactions nucléaires
Au cours d’une collision, il y a conservation de l’impulsion et de
l’énergie.
Mathématiquement, cela se traduit par la conservation des composantes
du quadrivecteur impulsion-énergie des particules avant le choc
avec celles du quadrivecteur impulsion-énergie des particules après
le choc.
Evidemment ces équations de conservation doivent être
écrites dans un même référentiel (dans la pratique,
celui du laboratoire ou celui du centre de masse des particules).
3. Relativité générale
Le problème de l’introduction de forces gravitationnelles (d’attraction
universelle) en Relativité n’a pas trouvé une solution simple.
Nos propos se limiteront aux idées et raisonnements à
la base de la théorie de la Relativité générale.
Dans le système solaire, l’observation de phénomènes
mettant en cause la Mécanique classique (newtonienne) est rare et
difficile tant cette théorie est en accord avec les phénomènes
couramment observables (mouvement des planètes).
Ainsi, pour expliquer, au début du 20ème siècle,
l’avance de périhélie de la planète Mercure, il était
plus " naturel " d’imaginer et de rechercher un satellite non connu de
cette planète.
Bien que l’on puisse faire un certain nombre d’analogies entre la force
d’attraction universelle et la force coulombienne, entre le champ d’attraction
universelle et le champ électrique, il est important de comprendre
que, dans le mouvement d’objets soumis à l’un ou l’autre de ces
champs, il existe une différence fondamentale : dans un même
champ gravitationnel, des objets différents ont même mouvement
(nous pensons, par exemple, à la chute libre, des corps ; pour
simplifier nous confondons dans ce propos gravitation et pesanteur)
alors que ce n’est pas le cas pour un même champ électrique.
Ceci doit être attribué au fait qu’aucune mesure, aussi
précise soit elle, n’a pu mettre en évidence une différence
entre la masse d’inertie d’un corps et sa masse gravitationnelle (appelée
aussi masse grave).
En ce sens, la force gravitationnelle se comporte comme la force d’inertie
(dont l’origine est un champ d’accélération) qui possède
cette propriété d’être proportionnelle à la
masse d’inertie. Cependant, il existe une différence importante
entre la force de gravitation et la force d’inertie : la première
s’évanouit lorsque la distance entre les corps en interaction augmente,
tandis que la seconde augmente lorsque l’on s’éloigne de l’axe de
rotation. Cette différence montre que c’est seulement localement
que le champ de gravitation peut être compensé par un champ
d’accélération. Ainsi, on peut simuler l’impesanteur dans
un satellite artificiel.
Ce résultat est connu, en Relativité générale,
sous le nom de principe d’équivalence : aucune expérience
ne peut révéler de différence entre un laboratoire
local accéléré et son analogue, fixe dans le référentiel
et soumis à un champ de gravitation.
Ce principe permet d’enlever, aux référentiels galiléens,
ce statut (insatisfaisant pour l’esprit) de référentiels
privilégiés (où s’applique le principe fondamental
de la dynamique).
En raison de l’analogie entre les forces d’inertie et de gravitation,
il paraît naturel de rechercher les raisons de ce " privilège
" dans la formulation classique de l’interaction gravitationnelle. Il est
logique de considérer, dans l’étude de la chute libre d’un
corps, que le référentiel " naturel " ne peut être
celui lié à la Terre, il doit être celui qui tombe
avec le corps.
Dans la théorie de la Relativité générale,
au lieu de considérer qu’une masse modifie le mouvement d’un corps
par la force gravitationnelle qu’elle exerce sur lui, on décrit
l’effet de cette masse par la modification qu’elle provoque dans la structure
de l’espace-temps. On considère qu’un référentiel
où les objets matériels sont soumis à la gravitation
se comporte comme un référentiel accéléré
et on modifie, en conséquence, la relation métrique qui définit
l’espace-temps.
On s’aperçoit que la notion de référentiel en
tant que système de coordonnées rigides doit être
abandonnée.
L’image que l’on donne, pour un système à deux dimensions
d’espace est la suivante : en Relativité générale,
le référentiel plan rigide est remplacé par une nappe
en caoutchouc souple ; la grosse masse " enfonce " la nappe en forme d’entonnoir
et une planète, soumise à aucune interaction (autre que la
gravitation), a une trajectoire fermée autour de la grosse masse.
La théorie de la Relativité générale a
reçu un certains nombre de confirmation dans le domaine de l’astrophysique
(avance de périhélie de Mercure, déviation gravitationnelle
de la lumière, trous noirs, décalage spectral gravitationnel).
Les théories s’appuyant sur la force gravitationnelle (en considérant,
pour le photon, une interaction gravitationnelle possible à partir d’une
masse en " vol " égale à 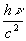 )
donnent des résultats satisfaisants sur le plan qualitatif mais faux
sur le plan quantitatif sauf en ce qui concerne la formule du décalage
spectral gravitationnel.
)
donnent des résultats satisfaisants sur le plan qualitatif mais faux
sur le plan quantitatif sauf en ce qui concerne la formule du décalage
spectral gravitationnel.
Décalage spectral gravitationnel
 |
Dans un référentiel (R) soumis à
un champ de gravitation  ,
une source S émet une onde électromagnétique vers un
observateur O. Ce problème est équivalent à celui de
l’émission par la source vers l’observateur dans un référentiel
(R’) non soumis à la gravitation mais animé par rapport à
(R) d’une accélération ,
une source S émet une onde électromagnétique vers un
observateur O. Ce problème est équivalent à celui de
l’émission par la source vers l’observateur dans un référentiel
(R’) non soumis à la gravitation mais animé par rapport à
(R) d’une accélération  . . |
L’onde atteint l’observateur après un temps 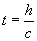 si h est la distance source-observateur. Dans le système équivalent,
la vitesse de l’observateur par rapport à (R) est
si h est la distance source-observateur. Dans le système équivalent,
la vitesse de l’observateur par rapport à (R) est  et, donc à l’instant t où l’observateur reçoit l’onde,
ce dernier se rapproche à cette vitesse.
et, donc à l’instant t où l’observateur reçoit l’onde,
ce dernier se rapproche à cette vitesse.
En remarquant que  représente l’énergie potentielle massique de l’observateur et
en appliquant la formule de l’effet Doppler-Fizeau,
représente l’énergie potentielle massique de l’observateur et
en appliquant la formule de l’effet Doppler-Fizeau,
on obtient :  où
où  sont les fréquences respectives pour la source et pour l’observateur.
sont les fréquences respectives pour la source et pour l’observateur.
Pour le champ de gravitation terrestre, l’expérience a pu être
faite en 1960 par Pound et Rebka, elle a été affinée en
1964 par Pound et Snider (variation relative de fréquence :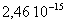 pour
pour 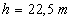 ).
).
On peut aussi en conclure que la marche des horloges dépend
du potentiel de gravitation dans lequel elle se trouve.
Le décalage spectral, vers le violet pour le cas ci-dessus du
potentiel de gravitation, se produit vers le rouge si on inverse les positions
de la source et de l’observateur (par exemple, observation à partir
de la terre du rayonnement émis par une étoile dans le champ
de gravitation qu’elle crée).
Mouvement d’une particule dans le voisinage d’une masse à
symétrie sphérique
Dans un référentiel à coordonnées polaires planes
(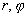 ), on obtient (sans
démonstration) l’équation différentielle :
), on obtient (sans
démonstration) l’équation différentielle : 
Par rapport à la Mécanique classique, il apparaît en plus
le terme  .
.
La résolution (laissée au soin du lecteur) explique parfaitement
les avances de périhélie des planètes du système
solaire ou la déviation de la lumière (cas 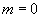 )
au voisinage du Soleil.
)
au voisinage du Soleil.



 ;
;  ;
; 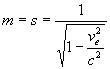 .
. 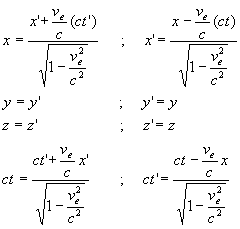
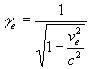 .
.
 ;
; 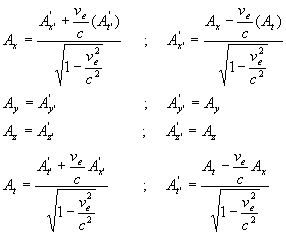
 ;
; 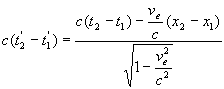
 ;
; 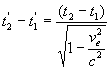
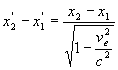 ;
; 
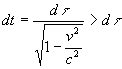 il y a dilatation du temps.
il y a dilatation du temps.
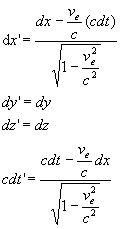
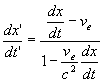 ;
;  ;
; 
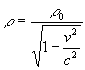
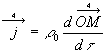 .
.
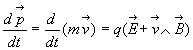 pour les forces électromagnétiques.
pour les forces électromagnétiques. 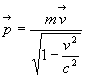 .
.
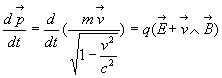 ,
la loi est possible, seule l’expérience la confirme.
,
la loi est possible, seule l’expérience la confirme.
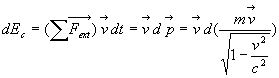
 .
.
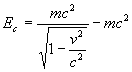 .
.
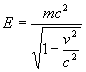 est l’énergie
de la particule.
est l’énergie
de la particule. 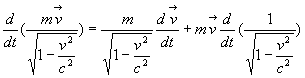 ,
,
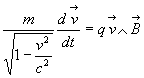 ,
, 
 ,
certains se croient obliger de parler de masse variant avec la vitesse (donc
aussi, de masse au repos), de masse transversale ou de masse longitudinale.
Ce langage ne présente aucun intérêt, pire certains y voient
quelques explications pseudoscientifiques.
,
certains se croient obliger de parler de masse variant avec la vitesse (donc
aussi, de masse au repos), de masse transversale ou de masse longitudinale.
Ce langage ne présente aucun intérêt, pire certains y voient
quelques explications pseudoscientifiques.
 est un quadrivecteur
dont les composantes sont
est un quadrivecteur
dont les composantes sont 