.Exercices de Cinématique des fluides
1) On demande de caractériser les écoulements bidimensionnels, permanents, ci-après définis par leur champ de vitesses.
a) .
b) 
c)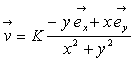 
d) 
| Réponse 1a | Réponse 1b | Réponse 1c | Réponse 1d |
2) On étudie la possibilité d’écoulements bidimensionnels,
isovolumes et irrotationnels.
On utilise, pour le repérage des particules du fluide, les coordonnées
polaires habituelles (
).
2)a) Montrer qu’il existe, pour cet écoulement, une fonction
potentiel des vitesses 
,
solution de l’équation aux dérivées partielles de Laplace
.
On étudie la possibilité de solutions élémentaires
où le potentiel
ne dépend soit que de 
,
soit que de 
.
2)b) 
Calculer le champ des vitesses. Après avoir précisé la
situation concrète à laquelle cette solution s’applique, calculer
le débit de l’écoulement.
2)c) 
Calculer
le champ des vitesses. Préciser la situation concrète à
laquelle cette solution s’applique.
| Réponse 2a | Réponse 2b | Réponse 2c |
3) On considère un fluide parfait parfait (viscosité nulle), incompressible (air à des faibles vitesses d’écoulement) de masse volumique m entourant un obstacle cylindrique de rayon R et d’axe Oz.
|
L’écoulement est à deux dimensions (vitesses
parallèles au plan xOy et indépendantes de z)
et stationnaire. Un point M du plan xOy est repéré
par ses coordonnées polaires |
|
3)1) Déduire que 
et que 
.
3)2) Ecrire les conditions aux limites satisfait par
le champ de vitesses 
au voisinage de l’obstacle (
),
à l’infini (
).
3)3) Montrer qu’une solution type 
est solution de 
.
En déduire l’équation différentielle vérifiée
par 
. Intégrer
cette équation différentielle en cherchant des solutions sous
la forme 
.
Calculer les deux constantes d’intégration et exprimer les composantes
du champ de vitesses 
.
3)4) Reprendre cet exercice en remplaçant le
cylindre par une sphère de rayon R.
On remarquera que le problème a une symétrie autour de l’axe des
x. On rappelle qu’en coordonnées sphériques, compte tenu
de la symétrie de révolution autour de l'axe des x, 
| Réponse 31 | Réponse 32 | Réponse 33 | Réponse 34 |
.
.