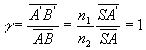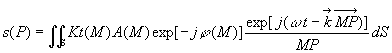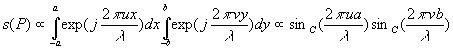Optique géométrique et Diffraction
1. Approximation " Optique géométrique
"
1.1. Le théorème de Malus
On considère un milieu diélectrique linéaire, isotrope
(qui peut être non homogène) caractérisé en chaque
point par sa permittivité électrique.
On se propose d’étudier la propagation, dans ce milieu, d’ondes électromagnétiques
de longueurs d’onde 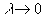 (lumière).
(lumière).
On cherche pour le champ électromagnétique des solutions sous
la forme :
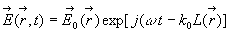
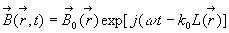 où
où 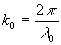 est le module du vecteur d’onde dans le vide et
est le module du vecteur d’onde dans le vide et 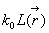 la phase.
la phase.
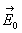 ,
, 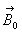 et
et 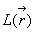 sont
des fonctions à déterminer dans le cas où
sont
des fonctions à déterminer dans le cas où 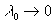 (en
fait où
(en
fait où 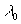 reste très inférieure à toute dimension spatiale).
reste très inférieure à toute dimension spatiale).
Le calcul, que nous ne reproduisons pas, montre que :
- 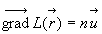 où
où 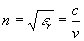 est l'indice de réfraction,
est l'indice de réfraction, 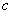 et
et 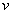 étant respectivement les intensités de vitesses de l’onde dans
le vide et dans le milieu au point considéré et
étant respectivement les intensités de vitesses de l’onde dans
le vide et dans le milieu au point considéré et 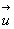 le vecteur unitaire de la direction de propagation de l'onde au point considéré,
le vecteur unitaire de la direction de propagation de l'onde au point considéré,
- 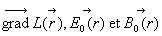 forment
un triède orthogonal direct.
forment
un triède orthogonal direct.
Les surfaces d’onde sont déterminées par 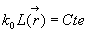 ,
si bien que la direction de la propagation se confond avec la direction de
,
si bien que la direction de la propagation se confond avec la direction de 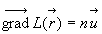 .
.
Ainsi, localement, dans le cas où 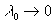 ,
l’onde a une structure d’onde plane.
,
l’onde a une structure d’onde plane.
1.2. Equation différentielle de la trajectoire d’un
rayon lumineux
En différentiant l’équation 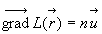 ,
on montre que l’équation de la trajectoire du rayon lumineux obéit
à l’équation :
,
on montre que l’équation de la trajectoire du rayon lumineux obéit
à l’équation : 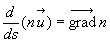 où
où 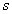 représente l’abscisse curviligne suivant la trajectoire..
représente l’abscisse curviligne suivant la trajectoire..
1.2.1. Milieu homogène
Pour un milieu d’indice n uniforme, on obtient 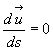 .
Le vecteur unitaire
.
Le vecteur unitaire 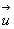 reste
identique à lui-même quelque soit la valeur de l’abscisse curviligne
: Les trajectoires suivies par la lumière dans un milieu homogène
sont des droites.
reste
identique à lui-même quelque soit la valeur de l’abscisse curviligne
: Les trajectoires suivies par la lumière dans un milieu homogène
sont des droites.
1.2.2. Exemple de milieu non homogène
On considère la trajectoire d’un rayon lumineux dans le plan
Oxy,
l’indice n étant une fonction de y.
Dans ce cas, 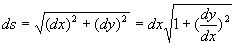 et
et 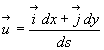 .
.
En projetant l’équation différentielle de la trajectoire,
on obtient :
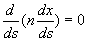 ð
ð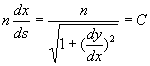 et
et 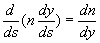
Par suite 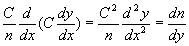 ,
soit
,
soit 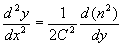 qui
établit explicitement l’équation différentielle de la trajectoire
du rayon lumineux.
qui
établit explicitement l’équation différentielle de la trajectoire
du rayon lumineux.
1.3. Le principe de Fermat
Entre deux surfaces d’onde voisines, la variation de phase est égale
à :
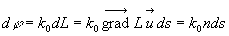
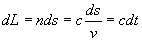 est, par définition,
la différentielle du chemin optique (
est, par définition,
la différentielle du chemin optique (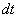 représente
le temps mis par la lumière pour aller d’une surface d’onde à
l’autre).
représente
le temps mis par la lumière pour aller d’une surface d’onde à
l’autre).
Nous avons vu que la trajectoire de la lumière est perpendiculaire, en
tout point, à la surface d’onde si bien que la longueur 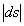 entre deux éléments correspondants de deux surfaces d’onde voisines
est minimale [
entre deux éléments correspondants de deux surfaces d’onde voisines
est minimale [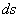 (ou
(ou 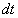 )
est minimal et positif s’il est compté dans le sens de propagation de
la lumière, maximal et négatif dans le sens contraire].
)
est minimal et positif s’il est compté dans le sens de propagation de
la lumière, maximal et négatif dans le sens contraire].
On appelle chemin optique entre deux points A et B d’une trajectoire
suivie par un rayon lumineux, la quantité 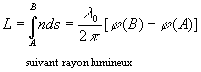
Le principe de Fermat exprime le caractère extrémal,
par " morceau " , du chemin optique de la manière suivante : le
chemin optique entre deux points A et B est stationnaire.
Il est courant de se servir du principe de Fermat comme point de
départ de l’Optique géométrique.
1.3.1. Milieu homogène
Dans un milieu d’indice n uniforme, la distance qui sépare
deux points d’un même rayon lumineux est minimale ð
la trajectoire est la droite qui joint les deux points.
Les trajectoires suivies par la lumière dans un milieu homogène
sont des droites.
1.3.2. Les lois de Descartes-Snell
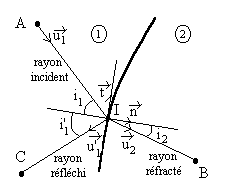 |
Sur le dessin ci-contre, est représentée
la trace de la surface de séparation entre les milieux homogènes
1 et 2 d’indices respectifs 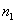 et
et 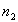 . .
Un rayon lumineux allant de A à B coupe la surface
de séparation en I dont on veut déterminer la position
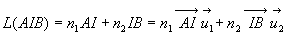
Ce chemin optique est stationnaire, c’est à dire que 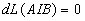 |
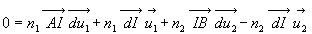
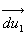 et
et 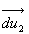 ,
vecteurs différentiels des vecteurs unitaires
,
vecteurs différentiels des vecteurs unitaires 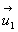 et
et 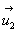 des directions
AI et IB, sont perpendiculaires à ces directions. Par suite,
des directions
AI et IB, sont perpendiculaires à ces directions. Par suite, 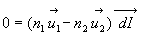
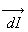 vecteur résultant
d’un déplacement élémentaire sur la surface de séparation
est dans le plan tangent en I à cette surface. Par suite,
vecteur résultant
d’un déplacement élémentaire sur la surface de séparation
est dans le plan tangent en I à cette surface. Par suite, 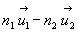 est
colinéaire à la direction normale en I à la surface
de séparation.
est
colinéaire à la direction normale en I à la surface
de séparation.
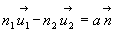 où
où 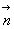 est
le vecteur unitaire de cette direction normale.
est
le vecteur unitaire de cette direction normale.
Le rayon réfracté est contenu dans le plan formé
par le rayon incident et la direction normale au point d’intersection à
la surface de séparation. Ce plan est appelé plan
d’incidence.
Si nous multiplions scalairement par le vecteur unitaire de la direction déterminée
par l’intersection du plan tangent et du plan incident, on obtient :
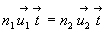 ð
ð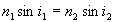 (dans cette formule, nous avons choisi de ne pas donner de caractère
algébrique aux angles
(dans cette formule, nous avons choisi de ne pas donner de caractère
algébrique aux angles 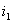 et
et 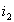 ð
rayon incident et rayon réfracté sont de part et d’autre de la
direction normale).
ð
rayon incident et rayon réfracté sont de part et d’autre de la
direction normale).
Ces résultats constituent les lois de la réfraction de Descartes-Snell.
En ce qui concerne la réflexion, c’est à dire le rayon
lumineux allant de A à C, il convient de changer 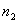 en
en 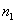 ,
, 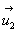 en
en 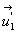 et
B en C.
et
B en C.
On trouve que le rayon réfléchi est dans le plan d’incidence
et que 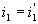 (dans
cette formule, les deux angles n’ont pas de caractère algébrique
ð rayon incident et rayon réfléchi
sont de part et d’autre de la direction normale).
(dans
cette formule, les deux angles n’ont pas de caractère algébrique
ð rayon incident et rayon réfléchi
sont de part et d’autre de la direction normale).
Ces résultats constituent les lois de la réflexion de Descartes-Snell.
1.3.3. Exemple de milieu non homogène
Par suite, 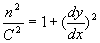 et,
après différentiation,
et,
après différentiation, 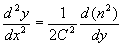
1.4. Le principe d’Huygens
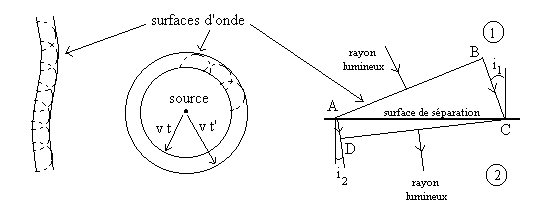
La lumière se propage de proche en proche. L’ensemble des
points d’égale perturbation lumineuse est appelée surface
d’onde . Chacun des points de cette surface atteints par la lumière
se comporte comme une source secondaire qui émet des ondelettes
sphériques dans un milieu isotrope. La surface enveloppe de ces
ondelettes forme une nouvelle surface d’onde.
Les dessins ci-dessus sont faits en supposant les milieux homogènes,
c’est à dire les indices ou les intensités de vitesse de propagation
uniformes dans chaque milieu.
Le dessin de droite permet de retrouver les lois de Descartes-Snell à
partir du Principe de Huygens.
Les surfaces d’onde AB et CD sont des plans (ondes planes). Dans
chacun des milieux notés 1 et 2, les surfaces d’onde sont parallèles
les unes au autres, la distance séparant deux surfaces d’onde d’un même
milieu étant 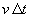 si
si 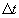 est le
temps mis pour la lumière pour aller à vitesse
est le
temps mis pour la lumière pour aller à vitesse 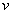 d’une surface d’onde à l’autre.
d’une surface d’onde à l’autre.
Dans le milieu 1, la lumière parcourt la distance 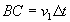 et, dans le même temps, la lumière parcourt, dans le milieu 2,
la distance
et, dans le même temps, la lumière parcourt, dans le milieu 2,
la distance 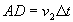 .
.
Des considérations géométriques simples permettent d’établir
la relation 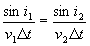 ,
soit
,
soit 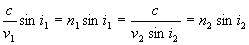 .
.
1.5. La formation des images
Un instrument d’optique est un assemblage de milieux " transparents
" à la lumière.
Le rôle des instruments d’optique est de donner des répliques,
appelées images, les plus fidèles et les plus grandes
possibles des objets. Un instrument fait converger les rayons lumineux
issus d’un point objet A vers un point A’. On dit
que A’ est l’image de A, ou le conjugué
de A, ou que l’instrument est stigmatique pour le couple
de points A, A’.
Bien que ce propos ne soit pas absolu, les rayons optiques " utiles
" seront peu inclinés par rapport à un axe appelé
axe
optique qui, souvent, est axe de révolution pour les instruments
d’optique (on parle alors de systèmes optiques centrés).
Les détecteurs qui permettent de " visualiser " les images sont
excités par l’énergie de l’onde. Le lecteur pourra se reporte
au chapitre " Photométrie et détecteurs ".
1.5.1. Stigmatisme
rigoureux
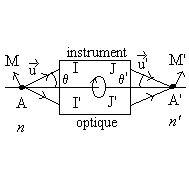 |
L’objet A ponctuel est dans un milieu d’indice 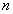 ,
l’image ponctuelle A’ dans un milieu d’indice ,
l’image ponctuelle A’ dans un milieu d’indice 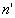 . .
Lorsque les rayons convergent vers l’image, celle-ci est réelle
c’est à dire capable " d’impressionner " un détecteur. Si
les rayons sont issues de A’ qui est à l’intérieur
de l’instrument, l’image est dite virtuelle.
Par extension, on parlera d’objet virtuel si les rayons convergent
vers " l’objet A " à l’intérieur de l’instrument. |
Le principe de Fermat (nous pourrions dire aussi que A et A’
sont deux surfaces d’onde ponctuelles) impose que le chemin optique 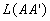 soit
indépendant du rayon.
soit
indépendant du rayon.
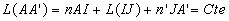 constitue la relation
de stigmatisme pour le couple A, A’.
constitue la relation
de stigmatisme pour le couple A, A’.
Le miroir plan est le seul instrument où la relation ci-dessus
est parfaitement réalisée quelque soit le couple A,
A’.
Dans le cas de systèmes simples tels que le miroir ellipsoïdal,
le miroir parabolique, le miroir sphérique ou le dioptre sphérique,
cette condition est réalisée pour un couple particulier de
points A, A’ appelés points d’Young ou de Weierstrass.
Le stigmatisme rigoureux ne présente qu’un intérêt
limité, d’autant que pour le réaliser, dans la pratique,
il faudrait empêcher le phénomène de diffraction
qui élargit l’image d’un point et disposer de cellules de détection
ponctuelles.
1.5.2. Stigmatisme
approché
Il est possible de réaliser des instruments optiques qui vérifient
la condition ci-dessus en première approximation.
Il s’agit de systèmes optiques dans lesquels on sélectionne
les rayons lumineux issus de l’objet A peu inclinés par rapport
à un axe appelé axe optique. Cette condition est appelée
approximation
de Gauss.
A priori, ces systèmes optiques sont à symétrie
de révolution, c’est à dire nous serons dans le cadre très
important des systèmes optiques centrés. Le couple A,
A’
est sur l’axe optique que nous notons axe z.
Avant d’aborder l’étude des éléments constitutifs
de ces systèmes optiques, il convient de savoir s’il peut y avoir
conservation du stigmatisme approché dans l’espace c’est à
dire existence de points conjugués en dehors de l’axe optique de
façon que objet et image conjugués ne se limitent pas à
des segments situés sur l’axe optique … ce qui ne présenterait
guère d’intérêt.
Stigmatisme approché dans l’espace
Sur la figure ci-dessus, nous envisageons le stigmatisme pour un couple
M,
M’
voisins de l’axe optique et d’un couple A, A’ situé
sur l’axe et vérifiant, au moins en première approximation,
la relation de stigmatisme 
Pour le couple M, M’ s’il est conjugué: 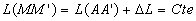 ,
soit encore
,
soit encore 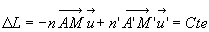
-
Aplanétisme : condition des sinus d’Abbe
On appelle plans frontaux des plans xy perpendiculaires à
l’axe optique z.
M, M’, que nous appelons B, B’, sont dans
des plans frontaux.
La condition ci-dessus devient 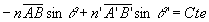 .
.
Pour calculer la constante, il suffit de prendre le rayon particulier correspondant
à 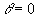 (donc
(donc 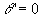 ).
).
On obtient la condition des sinus d’Abbe : 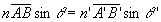
- Condition d’Herschel
M, M’, que nous appelons C, C’, sont sur l’axe optique.
La condition ci-dessus devient 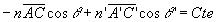 .
.
Pour calculer la constante, il suffit de prendre le rayon particulier correspondant
à 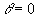 (donc
(donc 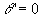 ).
).
On obtient la condition d’Herschel : 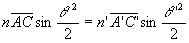
Ces deux conditions ne peuvent être réalisées en même
temps, aussi un stigmatisme tridimensionnel n’est pas possible.
1.6. Systèmes centrés
1.6.1. Eléments constitutifs d’un système centré
Les éléments constitutifs sont : les miroirs plans, les
miroirs sphériques, les dioptres plans et les dioptres sphériques.
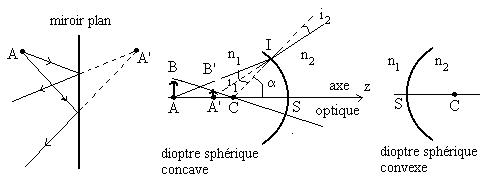
Le dessin du miroir plan montre que l’image A’ (virtuel) est
symétrique de l’objet A par rapport au miroir. Tout rayon
issu de A passe par A’ : il y a stigmatisme rigoureux.
Le dessin du dioptre sphérique sera utilisé pour
établir les " relations de conjugaison " entre les points
A
et A’, les résultats sont transposables sans difficulté
aux autres éléments constitutifs des systèmes centrés.
Dans les triangles AIC et A’IC, on écrit les relations
des sinus,
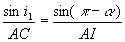 ;
; 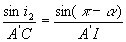 ð
ð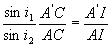 ð
ð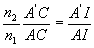 en introduisant la relation de Descartes-Snell de la réflexion.
en introduisant la relation de Descartes-Snell de la réflexion.
Cette relation doit être vérifiée quelque soit
I
(c’est à dire pour tout rayon lumineux) pour qu’il y ait stigmatisme
pour un couple A, A’ .
-
Le stigmatisme rigoureux est obtenu :
- pour tout point A sur le dioptre (A, I et A’
sont confondus)
- pour 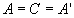
- pour un couple de points particuliers A, A’ appelés
points
de Weierstrass ou d’Young situés sur l’axe optique
z.
-
Le stigmatisme approché est réalisé pour un couple
de points A, A’ si les rayons sont peu inclinés sur
l’axe optique z (approximation de Gauss) ; en première approximation,
les points I peuvent être confondus avec le sommet S
du dioptre sphérique.
La formule, écrite sous forme algébrique, devient 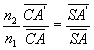 .
.
A l’aide de la relation de Chasles, on établit les relations
de conjugaison en prenant pour origine soit le sommet S, soit le centre
C du dioptre :
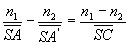 ou
ou 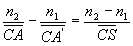
Un objet 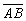 perpendiculaire
à l’axe optique forme une image
perpendiculaire
à l’axe optique forme une image 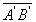 perpendiculaire
à l’axe optique.
perpendiculaire
à l’axe optique.
En utilisant le rayon BC, qui n’est pas dévié à
la traversée du dioptre, on calcule le grandissement linéaire 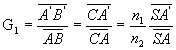
Miroir sphérique, dioptre plan et miroir plan
- Pour le miroir sphérique, on obtient les relations de conjugaison
et le grandissement à partir des résultats du dioptre sphérique
en remplaçant
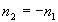 (cette astuce permet d’écrire les lois de la réflexion à
partir de celles de la réfraction).
(cette astuce permet d’écrire les lois de la réflexion à
partir de celles de la réfraction).
On obtient : 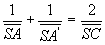 ;
; 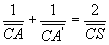 ;
; 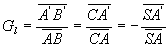
-
Le dioptre plan est un dioptre sphérique de rayon infini.
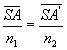 ;
; 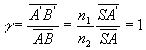
-
Le miroir plan s’obtient soit à partir du miroir sphérique,
soit à partir du dioptre plan .
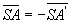 ;
; 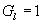
1.6.2. Eléments cardinaux d’un système centré.
Construction d’images. Relations de conjugaison
Foyers, Plans focaux
On appelle foyer objet F un point de l’axe optique tel
que tout rayon incident issu de F émerge après traversée
du système centré parallèlement à l’axe optique.
Le plan focal objet est le plan frontal Fxy.
On appelle foyer image F’ un point de l’axe optique tel
que tout rayon incident parallèle à l’axe optique émerge
en convergeant vers F’. Le
plan focal image est le plan frontal
F’xy.
Plans principaux
Ce sont des plans frontaux conjugués tel que le grandissement 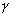 soit
égal à 1. Ils sont notés respectivement Hxy
(plan principal objet) et H’xy (plan principal image).
soit
égal à 1. Ils sont notés respectivement Hxy
(plan principal objet) et H’xy (plan principal image).
Focales
On appelle respectivement focale objet f et focale
image f’ les quantités algébriques : 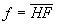 et
et 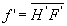 .
.
Construction d’images
Savoir construire des rayons est essentiel en Optique géométrique.
Pour le système optique l’indice est 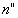 ,
pour les rayons incidents issus des objets l’indice est
,
pour les rayons incidents issus des objets l’indice est 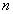 ,
pour les rayons émergents convergeant vers les images l’indice est
,
pour les rayons émergents convergeant vers les images l’indice est 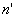 .
.
Sur l’axe optique sont connus les foyers F et F’ et les
points H et H’ des plans principaux objet et image : ils
définissent le système optique.
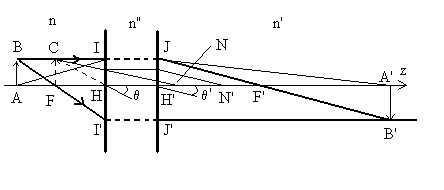
- Les deux rayons les plus importants sont (BIJF’B’) et (BFI’J’B’)
(BIJF’B’) : nous partons d’un objet AB et traçons par B
la parallèle à l’axe optique qui coupe le plan principal objet
en I. L’image de I est J dans le plan principal image telle que 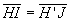 par
définition des plans principaux. Le rayon émergent du système
optique passe par le foyer image F’ puisque le rayon incident est parallèle
à l’axe optique.
par
définition des plans principaux. Le rayon émergent du système
optique passe par le foyer image F’ puisque le rayon incident est parallèle
à l’axe optique.
(BFI’J’B’) : nous partons de B et traçons BF qui
coupe le plan principal objet en I’. L’image de I’ est J’dans
le plan principal image telle que 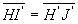 .
Le rayon émergent est parallèle à l’axe optique puisque
l’incident passe par le foyer objet F.
.
Le rayon émergent est parallèle à l’axe optique puisque
l’incident passe par le foyer objet F.
L’intersection des deux rayons définit B’ et donc l’image 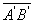 de l’objet
de l’objet 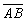 .
.
L’obtention des premières relations de conjugaison relève
de géométrie élémentaire :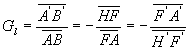 ;
; 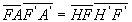 (relation
de Newton)
(relation
de Newton)
Il convient de ne pas oublier la très importante relation
des sinus d’Abbe 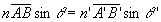 qui, dans le cadre de l’approximation de Gauss, est appelée relation
de Lagrange-Helmholtz et s’écrit
qui, dans le cadre de l’approximation de Gauss, est appelée relation
de Lagrange-Helmholtz et s’écrit 
- Nous considérons maintenant un objet
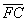 dans le plan focal objet, son image se forme à l’infini.
dans le plan focal objet, son image se forme à l’infini.
Nous avons déjà tracé le rayon (CIJF’).
L’image de l’objet H est H’. Le rayon émergent à
partir de H’, ayant pour incident (CH) est parallèle à
JF’ de façon que l’image se forme à l’infini.
On appelle 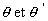 les
angles de ces rayons avec l’axe optique.
les
angles de ces rayons avec l’axe optique.
La relation de Lagrange pour l’objet 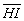 et son image
et son image 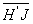 et pour les rayons définis s’écrit
et pour les rayons définis s’écrit 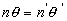 ð
ð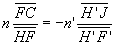 ð
ð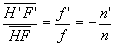
Pour des milieux extrêmes identiques 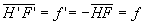
En transformant la relation de conjugaison de Newton à l’aide de la relation
mathématique de Chasles et en utilisant cette relation entre indices
et focales, on obtient : 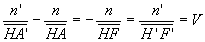 (V est appelée la vergence du système centré
et se mesure en dioptries dans le système MKS ; le système est
convergent si la vergence est positive, divergent si la vergence est négative).
(V est appelée la vergence du système centré
et se mesure en dioptries dans le système MKS ; le système est
convergent si la vergence est positive, divergent si la vergence est négative).
La relation de Lagrange-Helmholtz pour l’objet 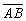 et l’image
et l’image 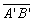 ,
pour le rayon incident AI et son émergent JA’ donne
,
pour le rayon incident AI et son émergent JA’ donne 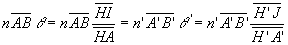 .
.
Après simplification, 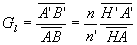 .
.
-
Enfin, nous déterminons les points nodaux N et N’
qui sont deux points conjugués définis comme étant
les intersections avec l’axe optique d’un incident et d’un émergent
parallèle.
A partir de C nous traçons un rayon incident parallèle
au rayon JF’ qui coupe le plan principal objet. L’émergent
au point conjugué du plan principal image est parallèle aux
deux rayons puisque l’image de l’objet 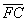 est à l’infini. Les intersections avec l’axe optique de ces deux
rayons donnent les points nodaux.
est à l’infini. Les intersections avec l’axe optique de ces deux
rayons donnent les points nodaux.
La connaissance des points nodaux est une façon de définir
un système optique qui peut se substituer à la connaissance
des plans principaux.
On remarquera que 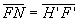 et que
et que 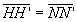
Très souvent les milieux où se propagent les rayons incident
et émergent sont identiques (généralement air) et 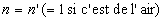
Remarques :
- pour le dioptre sphérique ou le miroir sphérique les plans principaux
sont confondus de telle sorte que 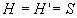 ,
,
- pour le dioptre sphérique ou le miroir sphérique les
points nodaux sont confondus au centre C,
- pour le dioptre sphérique, les focales sont 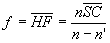 et
et 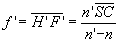 ,
,
- pour le miroir sphérique, les focales sont 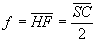 et
et 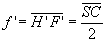 .
.
1.6.3. Un exemple de système centré : la
lentille mince
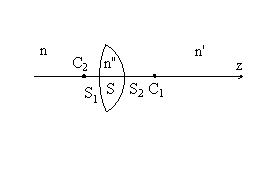 |
Une lentille mince est constituée de deux
dioptres sphériques comme indiqué sur la figure ci-contre
où on peut faire 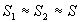 . .
Les plans principaux des deux dioptres sont des plans frontaux situés
en S. Il en sera de même pour la lentille mince (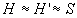 ). ).
Un objet A donne une image A" à travers le premier
dioptre qui sert d’objet à travers le deuxième dioptre pour
une image A’. |
L’écriture des formules de conjugaison donne :
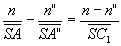 ;
; 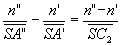 ð
ð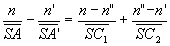
Le foyer objet et la focale objet seront déterminées par :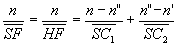 ,
le foyer image et la focale image par :
,
le foyer image et la focale image par : 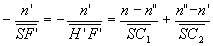
Les constructions de rayons et les résultats sur les systèmes
centrés du paragraphe précédent sont totalement transposables
en faisant 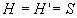 .
.
Très souvent les milieux extrêmes sont l’air ambiant (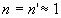 )
et l’indice du système optique est noté
)
et l’indice du système optique est noté 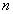 .
.
Avec ces nouvelles notations 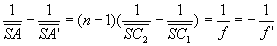
1.7. Aberrations
1.7.1. Aberration chromatique
L’indice des verres constituant les instruments optiques varie avec
la fréquence de l’onde lumineuse (ce phénomène est
appelé dispersion) si bien que les caractéristiques
varient : on dit que l’instrument présente une aberration chromatique.
Dans le cas d’une lentille mince, 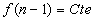 ð
ð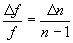 .
.
Conventionnellement, on utilise les trois radiations caractéristiques
suivantes : la radiation C rouge (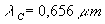 ),
la radiation F bleu-vert (
),
la radiation F bleu-vert (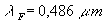 ),
toutes deux de l’atome d’Hydrogène) et la radiation D jaune (
),
toutes deux de l’atome d’Hydrogène) et la radiation D jaune (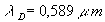 )
de l’atome de sodium et on définit le pouvoir dispersifK
(ou son inverse le nombre d’Abbe ou constringenceA) par
la relation :
)
de l’atome de sodium et on définit le pouvoir dispersifK
(ou son inverse le nombre d’Abbe ou constringenceA) par
la relation : 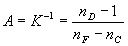 .
.
Il existe deux grands types de verre, les flints lourds qui
dispersent beaucoup (A est compris entre 30 et 50), les crowns
légers qui dispersent moins (A est compris entre 50 et 65).
Pour diminuer l’aberration chromatique, les lentilles sont en fait
l’assemblage de deux lentilles l’une en verre flint, l’autre en verre crown.
1.7.2. Aberrations géométriques ou monochromatiques
Dans l’approximation de Gauss, on linéarise les équations
en confondant sinus, tangente et angle. Les aberrations géométriques
(appelées aussi monochromatiques par opposition à chromatiques)
sont liées à cette approximation.
On se contentera de savoir qu’il en existe de plusieurs sortes.
2. Phénomène de Diffraction
En Optique géométrique, on cherche dans quelles conditions
l’image d’un objet ponctuel est aussi ponctuelle que possible.
Cependant, nous avons noté que cette recherche était
vaine ou limitée, le phénomène de diffraction élargissant
l’image.
Le phénomène de diffraction intervient dans des domaines
de la physique autres que l’optique. Nous pensons aux ondes électromagnétiques
radioélectriques et à la diffraction des électrons
sur les cristaux.
Les méthodes, que nous allons exposer, sont transposables.
2.1. Mises en évidence expérimentales
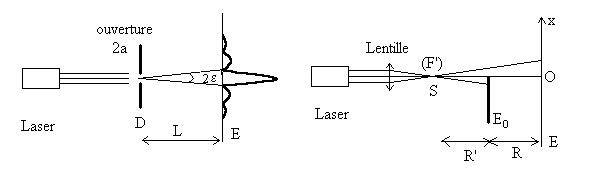
2.1.1. Diffraction par des petites ouvertures
Le diaphragme D est une fente fine de largeur 2a, de longueur
grande.
Le faisceau sortant du laser étant parallèle, on pourrait
s’attendre, d’après l’optique géométrique, à
obtenir sur l’écran une tache de largeur 2a.
Il n’en est rien et on constate, au contraire que la tache de lumière
sur l’écran s’élargit lorsque a diminue. En examinant
la répartition de l’intensité lumineuse sur l’écran,
on constate qu’elle présente une " structure " : on observe une
tache centrale entourée de taches secondaires beaucoup moins intenses.
La largeur angulaire de la tache centrale est égale à 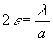 si
si 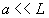
Pour  ,
, 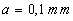 et
et 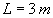 , on obtient
une largeur de tache centrale sur l’écran d’environ
, on obtient
une largeur de tache centrale sur l’écran d’environ 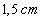 ,
c’est à dire que le phénomène de diffraction est facilement
visible
,
c’est à dire que le phénomène de diffraction est facilement
visible
2.1.2. Diffraction par le bord d’un écran
Dans cette expérience, si on s’en tenait à l’optique géométrique,
seule une partie de l’écran dans la partie des x positifs devrait
être éclairée. Il n’en est rien, la partie des x
négatifs est éclairée, l’intensité lumineuse diminuant
rapidement en s’éloignant du centre. Dans la partie des x positifs,
l’intensité lumineuse est modulée suivant un paramètre
de longueur égale à 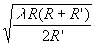 .
.
2.1.3. Strioscopie
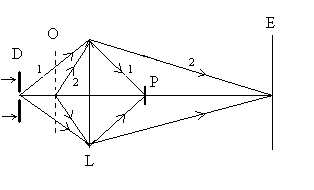 |
Par rapport à la lentille L, D (diaphragme)
et P (pastille opaque) sont conjugués, de même l’objet O (de
type plume, grillage, …) et l’écran E sont conjugués.
Dans un premier temps, nous ne plaçons pas l’objet O, le résultat
est évident, il n’y a pas de lumière sur l’écran E.
Dans un deuxième temps, nous plaçons l’objet O, le résultat
surprend, on observe son image, avec des contrastes très marqués,
sur l’écran. |
Cette expérience dite de strioscopie suggère que
les
points de l’objet éclairé se comporte comme autant de sources
secondaires émettant de la lumière dans toutes les directions
au delà de l’objet.
On retrouve, suivant cette hypothèse, le principe de Huygens
que l’on complétera par les idées de Fresnel pour interpréter
les phénomènes de Diffraction.
2.2. Le principe d’Huygens-Fresnel
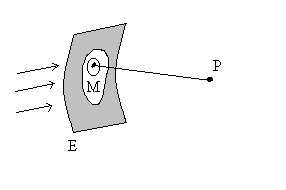 |
Nous reprenons la première expérience
de diffraction où dans un écran on a percé un diaphragme
: le fait expérimental est que l’état d’éclairement
en P est différent si l’écran existe ou non.
Suivant le principe d’Huygens, cela se comprend simplement puisque la
présence de l’écran élimine des " sources secondaires
" dont la lumière n’atteint plus P. |
Fresnel a précisé et étendu le principe d’Huygens.
Chaque point M d’une surface S atteinte par la lumière peut
être considéré comme une source secondaire émettant
une onde sphérique. L’état vibratoire de cette source secondaire
est proportionnel à celui de l’onde incidente en M et à l’élément
de surface dS entourant le point M. Les vibrations issues des différentes
sources secondaires interfèrent entre elles.
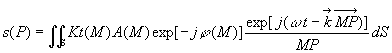
- 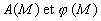 représentent
l’amplitude et la phase de l’onde incidente en M,
représentent
l’amplitude et la phase de l’onde incidente en M,
- 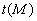 un coefficient
de transmission au niveau de la surface dS qui peut être partiellement
opaque [sauf indication, nous prendrons
un coefficient
de transmission au niveau de la surface dS qui peut être partiellement
opaque [sauf indication, nous prendrons 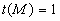 ],
],
- K un coefficient dépendant de la longueur d’onde de
l’onde mais surtout de la direction d’émission de la source secondaire
par rapport à la normale à la surface dS,
- 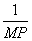 terme d’amortissement
du au fait qu’il s’agit d’ondes sphériques.
terme d’amortissement
du au fait qu’il s’agit d’ondes sphériques.
La démonstration mathématique rigoureuse du Principe d’Huygens-Fresnel
a fait l’objet de nombreuses recherches, en particulier par Kirchhoff, Rayleigh
ou Sommerfeld, sans réussite totale.
De toute façon, il faut voir dans cette relation un caractère
approché car il n’est pas tenu compte de l’interaction entre l’onde électromagnétique
et le matériau de l’écran.
Les recherches montrent que le coefficient K, pour une onde monochromatique,
peut être tenu pour constant si on reste voisin d’une direction. Ceci
revient à dire que les distances 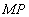 sont grandes devant les dimensions de la surface S (ce qui est le cas
puisque le phénomène de diffraction devient significatif lorsque
les dimensions de l’objet diffractant sont comparables à la longueur
d’onde) .
sont grandes devant les dimensions de la surface S (ce qui est le cas
puisque le phénomène de diffraction devient significatif lorsque
les dimensions de l’objet diffractant sont comparables à la longueur
d’onde) .
Aussi, dans le terme d’amortissement, les variations de 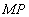 pour les différents points M de S seront sans conséquences
réelles, Par contre elles seront à considérer dans le terme
pour les différents points M de S seront sans conséquences
réelles, Par contre elles seront à considérer dans le terme 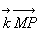 puisqu’à comparer avec la longueur d’onde.
puisqu’à comparer avec la longueur d’onde.
En fait, on ne calculera avec le principe d’Huygens-Fresnel que les variations
d’intensité (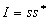 )
)
Sous ses considérations, la relation du principe d’Huygens-Fresnel peut
être écrite : 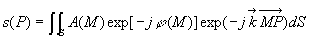
2.3. Théorème de Babinet (pour
en savoir plus par Yves Cortial)
Nous considérons deux surfaces diffractantes 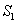 et
et 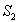 complémentaires
c’est à dire que la somme de ceux surfaces constituent un écran
total ne laissant pas passer la lumière au-delà.
complémentaires
c’est à dire que la somme de ceux surfaces constituent un écran
total ne laissant pas passer la lumière au-delà.
L’état vibratoire en P sera nul : 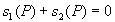 .
.
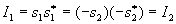
Les figures de diffraction de deux surfaces complémentaires
sont identiques.
2.4. Diffraction de Fresnel (à distance finie).
Diffraction de Fraunhofer (à l’infini)
Nous considérons une origine O située sur la surface S.
Compte tenu des domaines de validité de l’expression précédente 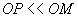 quelques
soient les points P ou M.
quelques
soient les points P ou M.
-
Pour un point P à distance finie, la direction du vecteur
d’onde
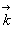 dépend des points M et P et on obtient, à partir
de la relation du principe d’Huygens, la formule (que nous n’établissons
pas) de diffraction de Fresnel.
dépend des points M et P et on obtient, à partir
de la relation du principe d’Huygens, la formule (que nous n’établissons
pas) de diffraction de Fresnel.
-
Pour un point P à " l’infini ", la direction du vecteur d’onde
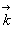 ne dépend pas des points M et P (le phénomène
de diffraction est produit dans une direction, les rayons parallèles
entre eux interfèrent à l’infini, on ramène l’observation
à distance finie dans le plan focal image d’une lentille)
ne dépend pas des points M et P (le phénomène
de diffraction est produit dans une direction, les rayons parallèles
entre eux interfèrent à l’infini, on ramène l’observation
à distance finie dans le plan focal image d’une lentille)
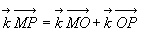 , ce dernier étant
constant son écriture n’est pas nécessaire dans la relation d’Huygens-Fresnel
qui devient :
, ce dernier étant
constant son écriture n’est pas nécessaire dans la relation d’Huygens-Fresnel
qui devient : 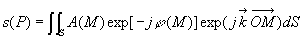 et constitue la relation de diffraction de Fraunhofer (à l’infini).
et constitue la relation de diffraction de Fraunhofer (à l’infini).
2.5. Diffraction à l’infini par une surface
plane
La surface plane est contenue dans le plan Oxy.
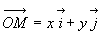 ;
; 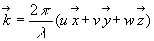 où u, v et w sont les cosinus directeurs du vecteur unitaire
de la direction du vecteur d’onde.
où u, v et w sont les cosinus directeurs du vecteur unitaire
de la direction du vecteur d’onde.
La formule de Fraunhofer devient : 
Application : fente rectangulaire
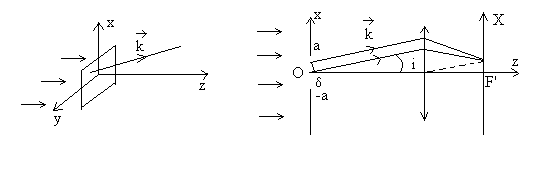
La fente rectangulaire a pour dimension 2a, 2b.
Nous prenons le cas simplificateur 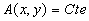 et
et 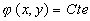 .
.
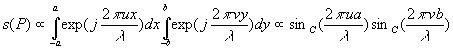
Ainsi, l’intensité lumineuse sera égale à 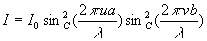
Pour des valeurs  ou
ou 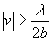 , l’intensité
lumineuse reste inférieure à
, l’intensité
lumineuse reste inférieure à 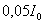 où
où 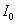 est l’intensité lumineuse pour
est l’intensité lumineuse pour 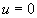 et
et 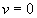 .
.
Ainsi, on considère que la tache lumineuse s’étale, en décroissant
d’une valeur maximale pour 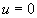 et
et 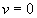 à
une valeur nulle sur les bords, sur des largeurs angulaires telles que
à
une valeur nulle sur les bords, sur des largeurs angulaires telles que 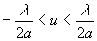 et
et 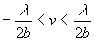 . On remarquera
que pour que les largeurs angulaires soient significatives, il faut que les
dimensions de la fente soient faibles.
. On remarquera
que pour que les largeurs angulaires soient significatives, il faut que les
dimensions de la fente soient faibles.
On appelle fente " infiniment longue " une fente telle que 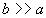 .
Dans ce cas, l’étalement de la tache est négligeable dans la direction
angulaire v, le phénomène de diffraction est sensible dans
la direction u.
.
Dans ce cas, l’étalement de la tache est négligeable dans la direction
angulaire v, le phénomène de diffraction est sensible dans
la direction u.
L’état vibratoire et l’intensité s’écrivent : 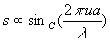 et
et 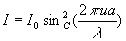
Dans ce cas, la composante du vecteur d’onde suivant la direction y n’intervient
pas et on peut se limiter à un vecteur d’onde dans le plan Oxy
tel que 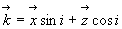
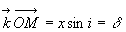 représente
la différence de marche entre les rayons diffractés suivant
la direction i passant par les abscisses 0 et x.
représente
la différence de marche entre les rayons diffractés suivant
la direction i passant par les abscisses 0 et x.
2.6. Pouvoir séparateur des instruments optiques
Les instruments optiques sont à symétrie de révolution
et nous prenons le cas simple d’une lentille de rayon R comme objet diffractant.
Le calcul de la figure de diffraction doit être fait dans le cas d’une
ouverture circulaire, il est mathématiquement plus complexe que celui
d’une ouverture rectangulaire et conduit à une tache de diffraction à
symétrie de révolution, appelée tache d’Airy, dont
seule la partie centrale d’angle angulaire 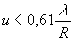 est réellement éclairée.
est réellement éclairée.
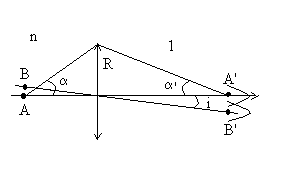 |
Nous supposons les objets A et B
suffisam-ment éloignés pour pouvoir appliquer la théorie
de la diffraction à l’infini. Ceci implique que les images A’
et B’ sont pratiquement dans le plan focal image à distance
f’
de la lentille.
Ces images sont en fait des taches d’Airy de largeur angulaire 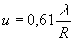 |
Ces deux taches seront distinctes si leur distance angulaire i
est supérieure à u, ceci revient à dire que
le maximum de lumière pour l’une est au moins au delà de
la limite de la tache de l’autre (critère de Lord Rayleigh).
Les deux objets seront vus distinctement si 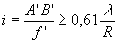 .
.
Les images sont dans l’air (indice égal à 1), par contre
les objets peuvent être, pour les microscopes à immersion,
dans un milieu d’indice n.
La relation de Lagrange-Helmholtz s’écrit 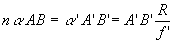 ð
ð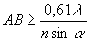 si on veut que les deux objets ponctuels soient vus distinctement.
si on veut que les deux objets ponctuels soient vus distinctement.
Cette formule montre que la limite inférieure de AB,
appelée pouvoir séparateur ou limite de résolution
de la lentille, est la plus faible possible si l’ouverture angulaire est
la plus grande possible (d’où la construction de télescope
de diamètre le plus grand possible) et si l’indice dans lequel sont
immergés les objets est le plus grand possible (d’où les
microscopes à immersion).
L’œil est, pour l’homme, l’organe sensoriel le plus important et
un Physicien ne saurait ne pas avoir des connaissances tangibles dans le
domaine de l’Optique.
Sans être exhaustif, dans le domaine de l’Optique géométrique,
on peut citer :
- mirage et arc en ciel en ce qui concerne les phénomènes
naturels,
- prisme, fibre optique, loupe, microscope, lunette astronomique,
télescope, appareil photographique en ce qui concerne les réalisations
pratiques.
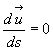 .
Le vecteur unitaire
.
Le vecteur unitaire 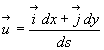 .
.
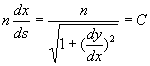 et
et 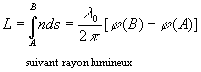

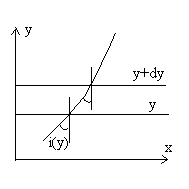
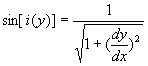



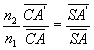 .
.
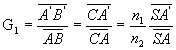
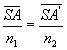 ;
;