L’approximation " Optique géométrique " consiste à étudier la propagation, dans ce milieu, d’ondes électromagnétiques de longueurs d’onde
On cherche pour le champ électromagnétique des solutions sous la forme :
Fibre optique
A) Généralités
A)1)
Approximation " Optique géométrique " : Le théorème de Malus
On considère un milieu diélectrique linéaire,
isotrope (qui peut être non homogène) caractérisé
en chaque point par sa permittivité électrique.
L’approximation " Optique géométrique " consiste
à étudier la propagation, dans ce milieu, d’ondes électromagnétiques
de longueurs d’onde ![]() .
.
On cherche pour le champ électromagnétique des solutions sous
la forme :
![]()
![]() où
où ![]() est
le module du vecteur d’onde dans le vide et
est
le module du vecteur d’onde dans le vide et ![]() la phase.
la phase.
![]() ,
,
![]() et
et ![]() sont
des fonctions à déterminer dans le cas où
sont
des fonctions à déterminer dans le cas où ![]() (en
fait où
(en
fait où ![]() reste très inférieure à toute dimension spatiale).
reste très inférieure à toute dimension spatiale).
Le calcul, que nous ne reproduisons pas, montre que :
Les surfaces d’onde sont déterminées par ![]() ,
si bien que la direction de la propagation (perpendiculaire en chaque point
à la surface d’onde) se confond avec la direction de
,
si bien que la direction de la propagation (perpendiculaire en chaque point
à la surface d’onde) se confond avec la direction de ![]() .
.
Ainsi, localement, dans le cas où ![]() ,
l’onde a une structure d’onde plane.
,
l’onde a une structure d’onde plane.
Le principe de Fermat
Entre deux surfaces d’onde voisines, la variation de phase
est égale à : ![]()
![]() est, par définition, la différentielle du chemin optique
(
est, par définition, la différentielle du chemin optique
(![]() représente
le temps mis par la lumière pour aller d’une surface d’onde à
l’autre).
représente
le temps mis par la lumière pour aller d’une surface d’onde à
l’autre).
La trajectoire de la lumière est perpendiculaire, en tout point, à
la surface d’onde si bien que la longueur ![]() entre deux éléments correspondants de deux surfaces d’onde voisines
est minimale [
entre deux éléments correspondants de deux surfaces d’onde voisines
est minimale [![]() (ou
(ou ![]() ) est minimal
et positif s’il est compté dans le sens de propagation de la lumière,
maximal et négatif dans le sens contraire].
) est minimal
et positif s’il est compté dans le sens de propagation de la lumière,
maximal et négatif dans le sens contraire].
On appelle chemin optique entre deux points A et B d’une
trajectoire suivie par un rayon lumineux, la quantité 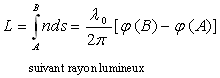
![]()
Le principe de Fermat exprime le caractère extrémal,
par " morceau " , du chemin optique de la manière
suivante : le chemin optique entre deux points A et B est stationnaire.
Il
est courant de se servir du principe de Fermat comme point de départ
de l’Optique géométrique.
A)2)
Les lois de Descartes-Snell
|
|
Sur le dessin ci-contre, est représentée
la trace de la surface de séparation entre les milieux homogènes
1 et 2 d’indices respectifs Ce chemin optique est stationnaire, c’est à dire que
|
![]()
![]() et
et ![]() , vecteurs
différentiels des vecteurs unitaires
, vecteurs
différentiels des vecteurs unitaires ![]() et
et ![]() des directions
AI et IB, sont perpendiculaires à ces directions. Par suite,
des directions
AI et IB, sont perpendiculaires à ces directions. Par suite,
![]()
![]() vecteur résultant
d’un déplacement élémentaire sur la surface de séparation
est dans le plan tangent en I à cette surface. Par suite,
vecteur résultant
d’un déplacement élémentaire sur la surface de séparation
est dans le plan tangent en I à cette surface. Par suite, ![]() est
colinéaire à la direction normale en I à la surface
de séparation.
est
colinéaire à la direction normale en I à la surface
de séparation.
![]() où
où ![]() est
le vecteur unitaire de cette direction normale.
est
le vecteur unitaire de cette direction normale.
Le rayon réfracté est contenu dans le plan formé par le rayon incident et la direction normale au point d’intersection à la surface de séparation. Ce plan est appelé plan d’incidence.
Si nous multiplions scalairement par le vecteur unitaire de
la direction déterminée par l’intersection du plan tangent et
du plan incident, on obtient :
![]() ð
ð
![]() (dans cette
formule, nous avons choisi de ne pas donner de caractère algébrique
aux angles
(dans cette
formule, nous avons choisi de ne pas donner de caractère algébrique
aux angles ![]() et
et ![]() ð rayon incident et rayon réfracté
sont de part et d’autre de la direction normale).
ð rayon incident et rayon réfracté
sont de part et d’autre de la direction normale).
Ces résultats constituent les lois de la réfraction de Descartes-Snell.
En ce qui concerne la réflexion, c’est à
dire le rayon lumineux allant de A à C, il convient de
changer ![]() en
en ![]() ,
,
![]() en
en ![]() et
B en C.
et
B en C.
On trouve que le rayon réfléchi est dans le
plan d’incidence et que ![]() (dans cette formule, les deux angles n’ont pas de caractère algébrique
ð rayon incident et rayon réfléchi
sont de part et d’autre de la direction normale).
(dans cette formule, les deux angles n’ont pas de caractère algébrique
ð rayon incident et rayon réfléchi
sont de part et d’autre de la direction normale).
Ces résultats constituent les lois de la réflexion de Descartes-Snell.
A)3)
Considérons ![]() avec
avec ![]() (le milieu
2 est moins réfringent que le milieu 1.
(le milieu
2 est moins réfringent que le milieu 1.
![]() (
(![]() )
)
Ainsi, tout rayon incident tel que ![]() ou
ou ![]() est réfléchi.
est réfléchi.
A)4)
Un instrument d’optique est un assemblage de milieux " transparents "
à la lumière.
Le rôle des instruments d’optique est de donner des répliques,
appelées images, les plus fidèles et les plus grandes possibles
des objets. Un instrument fait converger les rayons lumineux issus d’un
point objet A vers un point A’. On dit que A’ est
l’image de A, ou le conjugué de A, ou que
l’instrument est stigmatique pour le couple de points A, A’.
Bien que ce propos ne soit pas absolu, les rayons optiques " utiles "
seront peu inclinés par rapport à un axe appelé axe
optique qui, souvent, est axe de révolution pour les instruments
d’optique (on parle alors de systèmes optiques centrés).
Les détecteurs qui permettent de " visualiser " les
images sont excités par l’énergie de l’onde. Le lecteur pourra
se reporte au chapitre " Photométrie et détecteurs ".
Stigmatisme rigoureux
|
|
L’objet A ponctuel est dans un milieu d’indice
|
Le principe de Fermat (nous pourrions dire aussi que A
et A’ sont deux surfaces d’onde ponctuelles) impose que le chemin
optique ![]() soit indépendant
du rayon.
soit indépendant
du rayon.
![]() constitue la
relation de stigmatisme pour le couple A, A’.
constitue la
relation de stigmatisme pour le couple A, A’.
Le miroir plan est le seul instrument où la relation ci-dessus
est parfaitement réalisée quelque soit le couple A,
A’. Dans le cas de systèmes simples tels que le miroir ellipsoïdal,
le miroir parabolique, le miroir sphérique ou le dioptre sphérique,
cette condition est réalisée pour un couple particulier de points
A, A’ appelés points d’Young ou de Weierstrass.
Le stigmatisme rigoureux ne présente qu’un intérêt limité,
d’autant que pour le réaliser, dans la pratique, il faudrait empêcher
le phénomène de diffraction qui élargit l’image
d’un point et disposer de cellules de détection ponctuelles.
Stigmatisme approché
Il est possible de réaliser des instruments optiques
qui vérifient la condition ci-dessus en première approximation.
Il s’agit de systèmes optiques dans lesquels on sélectionne les
rayons lumineux issus de l’objet A peu inclinés par rapport à
un axe appelé axe optique. Cette condition est appelée
approximation de Gauss.
A priori, ces systèmes optiques sont à symétrie de révolution,
c’est à dire nous serons dans le cadre très important des systèmes
optiques centrés. Le couple A, A’ est sur l’axe optique
que nous notons axe z.
|
B)1) Pour qu’il y ait réflexion totale,
il convient que B)2)
B)3) |
|

Une fibre de 10m de longueur produira d’un objet ponctuel une tâche de 10cm : stigmatisme de faible qualité.
|
C)1) Axe de la fibre et rayon incident (entrant dans la fibre) définissent un plan radial qui contiendra le rayon réfracté. Si on considère dans ce plan, les lignes équi-indices
[
En reportant, |
|
C)2)
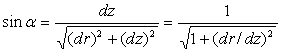
Soit 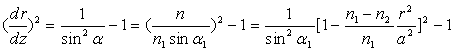
C)3)a)
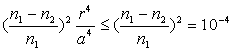
Ainsi, 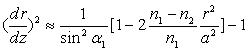 ð
ð
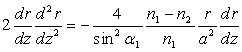
Soit l’équation différentielle de la trajectoire du rayon,
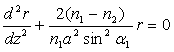 avec les deux
conditions aux limites
avec les deux
conditions aux limites ![]() et
et ![]() .
.
C)3)b)
La solution de l’équation différentielle est de la forme :
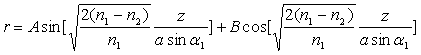
En tenant compte des conditions aux limites, on obtient :

C)3)c)
Pour qu’il y ait propagation, il convient que : 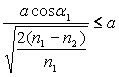 ð
ð 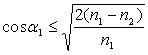
Soient ![]() et
et ![]()
C)3)d)
La périodicité de la fonction sinus impose que le rayon lumineux coupe régulièrement l’axe de la fibre en des points séparés de d tels que :
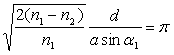 ð
ð
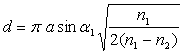
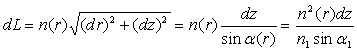
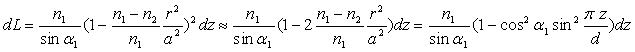

![]()
Soit ![]() ð
ð
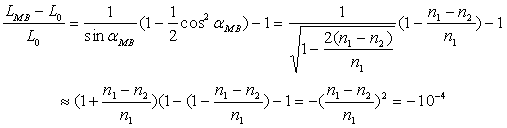
Une fibre de 10m de longueur produira d’un objet ponctuel une tâche de 1 mm : stigmatisme de bonne qualité.
C)3)e) Les angles d’ouverture sont identiques, la fibre à gradient d’indice est très supérieure à la fibre à saut d’indice
C)3)f) ![]()
C)3)g) Le milieu n’est pas parfaitement transparent ð il y a atténuation au cours de la propagation du signal lumineux
D)1)
|
Les formules de conjugaison donnent :
En retranchant membre à membre, |
|
Pour une lentille mince de sommet S, on obtient : ![]()
L’avantage essentiel d’une lentille-boule par rapport à une lentille
mince de même distance focale se situe au niveau des aberrations monochromatiques
(comportement pour différentes longueurs d’onde).
![]()