Fibre optique
| Les illustrations et animations de Yves
Cortial et Jacques
Charrier
La
fibre à saut d'indice
|
Problème
A) Généralités
1) Enoncer le principe de Fermat relatif au chemin optique d’un rayon lumineux.
2) Rappeler les lois de Descartes-Snell de la réfraction et de la réflexion.
3) Quand y a t’il réflexion totale à la surface de séparation de deux milieux transparents, homogènes et isotropes ?
4) Quelle est la définition d’un système stigmatique ?
B) Fibres à saut d’indice
Une fibre optique cylindrique, d’axe Oz, est constituée
d’un cœur transparent homogène et isotrope, de rayon a, d’indice
de réfraction ![]() ,
entouré d’une gaine, elle aussi transparente homogène et isotrope
dont l’indice de réfraction
,
entouré d’une gaine, elle aussi transparente homogène et isotrope
dont l’indice de réfraction ![]() est tel que
est tel que ![]() .
.
|
|
B)1) Montrer que l’angle B)2) En déduire que l’angle i à
l’entrée de la fibre doit rester inférieur à une
valeur |
B)3) Calculer, en fonction de ![]() ,
le chemin optique
,
le chemin optique ![]() correspondant à un angle d’incidence
correspondant à un angle d’incidence ![]() .
.
Montrer que la variation relative de chemin optique pour les rayons extrêmes
se propageant à travers la fibre optique est égale à 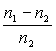 .
Application numérique.
.
Application numérique.
Que pensez-vous du stigmatisme de cette fibre ?
C) Fibres à gradient d’indice
Dans les fibres à gradient d’indice, l’indice du milieu
transparent, isotrope diminue de façon continue de la valeur ![]() sur l’axe à la valeur
sur l’axe à la valeur ![]() suivant une loi
suivant une loi 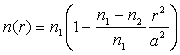 où r représente la distance à l’axe.
où r représente la distance à l’axe.
|
|
On considère un rayon lumineux entrant dans la fibre optique par un point O situé dans l’axe optique. C)1) Montrer que le rayon lumineux est contenu
dans le plan radial formé par l’axe de la fibre et le rayon incident
et que sa trajectoire obéit à la relation : |
C)2) Montrer que le trajet du rayon lumineux dans la fibre obéit à l’équation différentielle :
![]() [on montrera que
[on montrera que 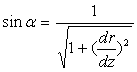 ]
]
C)3)a) Montrer, à partir des valeurs numériques,
que le terme 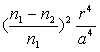 peut être négligé dans l’équation différentielle
précédente.
peut être négligé dans l’équation différentielle
précédente.
En déduire que la trajectoire du rayon lumineux obéit
à l’équation différentielle 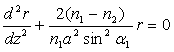 et
aux conditions aux limites
et
aux conditions aux limites ![]() et
et ![]() .
.
C)3)b) En déduire l’équation de la trajectoire
du rayon lumineux :
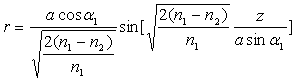
C)3)c) Montrer que l’angle ![]() doit être supérieur à une valeur que l’on exprimera en fonction
de
doit être supérieur à une valeur que l’on exprimera en fonction
de ![]() et
et ![]() pour qu’il y ait propagation.
pour qu’il y ait propagation.
En déduire que l’angle i à l’entrée de la fibre
doit rester inférieur à une valeur ![]() que l’on exprimera en fonction de
que l’on exprimera en fonction de ![]() et
et ![]() (on considérera
que l’indice de l’air est égal à 1).
(on considérera
que l’indice de l’air est égal à 1).
Application numérique : calculer ![]() .
.
C)3)d) Montrer que le rayon lumineux coupe l’axe Oz
en des points régulièrement espacés ; déterminer
la distance d séparant deux points consécutifs en fonction
de ![]() .
.
Montrer que la variation relative de chemin optique pour les rayons extrêmes
se propageant à travers la fibre optique est égale à 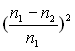 .
Application numérique.
.
Application numérique.
Que pensez-vous du stigmatisme de cette fibre ?
C)3)e) Comparer, du point de vue de la possibilité de propagation d’une onde, fibre à saut d’indice et fibre à gradient d’indice.
C)3)f) La grande directivité d’un laser permet
de donner à l’angle i des valeurs inférieures à
![]() . Quelle conclusion
peut on en tirer ?
. Quelle conclusion
peut on en tirer ?
C)3)g) Citer un facteur, passé sous silence, qui limite la longueur des liaisons assurées par fibres optiques.
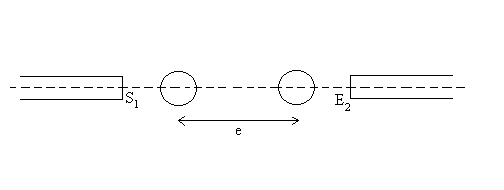
D) Couplage de deux fibres optiques
Pour coupler deux fibres optiques ![]() et
et ![]() , on utilise
un système de deux lentilles-boules
, on utilise
un système de deux lentilles-boules ![]() et
et ![]() identiques
de diamètre
identiques
de diamètre ![]() et d’indice
et d’indice ![]() .
.
D)1) Etude d’une lentille-boule
On appelle C le centre de la lentille-boule. Un point
objet A, situé sur l’axe optique forme une image ![]() à travers le premier dioptre sphérique ; cette image sert
d’objet pour le deuxième dioptre sphérique et forme une image
A’.
à travers le premier dioptre sphérique ; cette image sert
d’objet pour le deuxième dioptre sphérique et forme une image
A’.
A partir des formules de conjugaison écrites à partir du centre
C commun à chacun des dioptres sphériques, montrer que
la lentille-boule est équivalente à une lentille mince située
en C de distance focale image ![]() .
.
Voyez-vous des avantages à utiliser des lentille-boules plutôt
que des lentilles minces ?
D)2)a) Calculer la distance e entre les centres des deux lentille-boules pour que le système constitué de ces deux lentilles soit afocal. Application numérique.
D)2)b) la condition ci-dessus étant réalisée,
on place un objet ![]() dans le plan de sortie
dans le plan de sortie ![]() de la première fibre, ce plan étant confondu avec le plan focal
objet de la première lentille boule.
de la première fibre, ce plan étant confondu avec le plan focal
objet de la première lentille boule.
Le plan d’entrée ![]() de la deuxième fibre est confondu avec le plan focal image de la deuxième
lentille-boule.
de la deuxième fibre est confondu avec le plan focal image de la deuxième
lentille-boule.
A partir de la construction de rayons lumineux, montrer que l’image ![]() se forme dans le plan
se forme dans le plan ![]() ;
calculer le grandissement
;
calculer le grandissement ![]() .
.
| Réponse A1 | Réponse A2 | Réponse A3 | Réponse A4 | Réponse B1 | Réponse B2 | Réponse B3 | Réponse C1 | Réponse C2 | Réponse C3a | Réponse C3b | Réponse C3c | Réponse C3d | Réponse C3e | Réponse C3f | Réponse C3g | Réponse D1 | Réponse D2a | Réponse D2b |